 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Допущения элементарной теории гироскопов. Свойства гироскопа
Гироскопом называется симметричное твердое тело, быстро вращающееся вокруг оси симметрии (собственное вращение). Эта ось может менять свою ориентацию в пространстве. Примерами таких тел могут служить волчок с неподвижной точкой О (рис.4.1.а), гироскоп с двумя (рис.4.1.б) и тремя (рис.4.1.в) степенями свободы.
Благодаря ряду специфических свойств гироскопические устройства широко применяются в технике. Эти свойства можно достаточно полно объяснить с помощью элементарной (приближенной) теории гироскопов. Пусть однородное тело совершает быстрое вращение вокруг собственной оси симметрии с угловой скоростью Свяжем с телом координатную систему Оxyz так, чтобы ось Выражения для проекций кинетического момента тела на оси
где В общем случае направления векторов
Равенство (4.2) выражает основное допущение элементарной теории гироскопов: кинетический момент гироскопа направлен по собственной оси симметрии. Для изучения движения гироскопа (точнее – его оси) воспользуемся теоремой об изменении кинетического момента (2.18) в интерпретации Резаля: скорость конца вектора кинетического момента
Соотношение (4.3) позволяет найти закон движения оси гироскопа по заданному моменту внешних сил либо по заданному движению гироскопа определить момент сил, вызывающий такое движение. Рассмотрим основные свойства гироскопа с тремя степенями свободы, изображенного на рис.4.1.в. Если гироскоп уравновешен, то Отметим, что если подобрать специальным образом Другим важным свойством оказывается нечувствительность быстро вращающегося гироскопа к действию кратковременных сил. Причина - Все эти свойства гироскопов широко используются в системах навигации.
Поиск по сайту: |

 , а эта ось, в свою очередь, вращается с угловой скоростью
, а эта ось, в свою очередь, вращается с угловой скоростью  вокруг неподвижной оси (см. рис. 4.1.а). Для абсолютной угловой скорости
вокруг неподвижной оси (см. рис. 4.1.а). Для абсолютной угловой скорости  справедлива формула
справедлива формула  .
.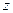 совпадала с осью собственного вращения; оси этой системы являются главными осями инерции тела.
совпадала с осью собственного вращения; оси этой системы являются главными осями инерции тела. и
и 

 , (4.1)
, (4.1) - соответствующие осевые моменты инерции тела.
- соответствующие осевые моменты инерции тела. и
и  не совпадают. Однако, если
не совпадают. Однако, если  , то
, то  и можно приближенно записать
и можно приближенно записать . (4.2)
. (4.2) равна главному моменту внешних сил относительно неподвижной точки О, т.е.
равна главному моменту внешних сил относительно неподвижной точки О, т.е. . (4.3)
. (4.3) и согласно (4.3)
и согласно (4.3)  . В таком случае ось гироскопа сохраняет неизменным свое направление в инерциальной координатной системе отсчета при любых движениях основания гироскопа. Отмеченное свойство оказывается полезным при конструировании гирогоризонталей и горовертикалей, а так же указателей направлений на условно неподвижные звезды.
. В таком случае ось гироскопа сохраняет неизменным свое направление в инерциальной координатной системе отсчета при любых движениях основания гироскопа. Отмеченное свойство оказывается полезным при конструировании гирогоризонталей и горовертикалей, а так же указателей направлений на условно неподвижные звезды. , можно добиться сохранения гироскопом неизменности направления своей оси и в неинерциальной системе отсчета (например, в системе отсчета, связанной с Землей). Последнее свойство используется при конструировании гирокомпасов.
, можно добиться сохранения гироскопом неизменности направления своей оси и в неинерциальной системе отсчета (например, в системе отсчета, связанной с Землей). Последнее свойство используется при конструировании гирокомпасов. только во время действия таких сил (в действительности после кратковременного действия сил ось гироскопа совершает затухающие малые нутационные колебания, которыми в элементарной теории гироскопов пренебрегают).
только во время действия таких сил (в действительности после кратковременного действия сил ось гироскопа совершает затухающие малые нутационные колебания, которыми в элементарной теории гироскопов пренебрегают).