 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема о движении центра масс механической системы
Центром масс С механической системы называется точка, радиус – вектор которой определяется из соотношения
где В случае выбора декартовой координатной системы
Формально для твердого тела центр тяжести и центр масс совпадают, хотя в принципе эти понятия различны. В основе понятия о центре тяжести лежит нахождение точки приложения равнодействующей параллельных сил тяжести. При нахождении положения центра масс вообще не говорится о действующих силах. Это понятие представляет собой одну из характеристик распределения масс в механической системе. В инерциальной системе отсчета для точек механической системы можно записать дифференциальные уравнения движения:
здесь После суммирования этих уравнений для всех точек механической системы получим
где Если теперь рассматривать только механические системы постоянного состава, состоящие из одних и тех же материальных точек с неизменными во времени массами
Окончательное выражение примет вид
При выборе декартовой координатной системы ему будут соответствовать три скалярных выражения:
Формула (2.6.а) есть запись теоремы: центр масс механической системы движется как материальная точка, масса которой равна массе всей механической системы, под действием силы, равной главному вектору действующих на эту систему внешних сил. Заметим, что формулы (2.6) не содержат внутренних сил, какими бы свойствами не обладала механическая система (жидкость, газ, упругое тело или твердое). Отмеченное обстоятельство существенно упрощает решение задач, так как позволяет исключить из рассмотрения обычно неизвестные внутренние силы. С другой стороны, отсутствие влияния на движение механической системы внутренних сил вызывает у студентов недоумение – ведь момент от двигателя, вращающий колеса автомобиля, есть внутреннее усилие, и, по сформулированной теореме, не может оказывать влияние на его движение! Рассуждения, вносящие ясность в этот вопрос, достаточно просты – на абсолютно гладкой поверхности (например, на льду) отсутствует сила сцепления и независимо от создаваемого мотором момента, вращающего ведущие колеса, автомобиль остается на месте. Если поверхность шероховатая, в выражение (2.6) должны войти силы сцепления, которые для автомобиля являются внешними. Очевидно, что при отсутствии момента, стремящегося вращать колеса автомобиля (двигатель не работает либо нажата педаль сцепления), эти силы возникать не будут и автомобиль никуда не уедет. Таким образом, хотя внутренние силы непосредственно в формулы (2.6) не входят, они могут вызвать внешние силы, которые в эти формулы должны войти. Из формулы (2.6.а) следует, что если главный вектор внешних сил окажется равным нулю, то должно быть равно нулю ускорение точки С. В этом случае в процессе движения механической системы скорость ее центра масс будет сохранять величину и направление. Если окажется, что равна нулю проекция на какую-либо координатную ось главного вектора внешних сил, то проекция на эту ось скорости центра масс будет постоянной. ПРИМЕР 2.1. На судне водоизмещением РЕШЕНИЕ. На рис.2.2 изобразим механическую систему (судно, груз А и балласт В) в исходном положении, а так же внешние силы, на нее действующие.
При отсутствии сопротивления воды проекция на горизонтальную ось Поскольку в начальный момент времени судно находилось в покое (т.е. Для начального положения механической системы
где Для конечного состояния системы
Приравнивая полученные выражения, найдем
Поиск по сайту: |
 , (2.4.а)
, (2.4.а)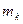 и
и  - масса и радиус – вектор
- масса и радиус – вектор  - ой материальной точки (
- ой материальной точки (  ) соответственно, а
) соответственно, а  - масса механической системы.
- масса механической системы.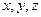 , векторное равенство (2.4.а) позволяет получить выражения для проекций радиуса – вектора центра масс С:
, векторное равенство (2.4.а) позволяет получить выражения для проекций радиуса – вектора центра масс С: ;
;  ;
;  . (2.4.б)
. (2.4.б) ;
; 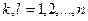 (2.5)
(2.5) - равнодействующая внутренних сил, действующих на
- равнодействующая внутренних сил, действующих на  ,
, и
и  - главные векторы внешних и внутренних сил, действующих на точки механической системы.
- главные векторы внешних и внутренних сил, действующих на точки механической системы. .
. ; (2.6.а)
; (2.6.а)
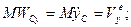 (2.6.б)
(2.6.б)
 груз А весом
груз А весом 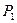 судовой грузовой стрелой перемещен в корму на расстояние
судовой грузовой стрелой перемещен в корму на расстояние 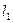 . Затем для частичного устранения возникшего дифферента жидкий балласт В весом
. Затем для частичного устранения возникшего дифферента жидкий балласт В весом  перемещен из кормовой цистерны в носовую на расстояние
перемещен из кормовой цистерны в носовую на расстояние  . Определить продольное перемещение
. Определить продольное перемещение  судна из состояния покоя, считая сопротивление воды пренебрежимо малым.
судна из состояния покоя, считая сопротивление воды пренебрежимо малым.
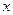 главного вектора внешних сил равна нулю, следовательно равна нулю горизонтальная составляющая ускорения центра масс. В этом случае горизонтальная составляющая скорости центра масс механической системы должна быть неизменной в процессе грузовой операции.
главного вектора внешних сил равна нулю, следовательно равна нулю горизонтальная составляющая ускорения центра масс. В этом случае горизонтальная составляющая скорости центра масс механической системы должна быть неизменной в процессе грузовой операции. ), то абсцисса
), то абсцисса  центра масс механической системы в процессе грузовой операции должна сохранять свою величину. Приравняв абсциссы центра масс для начального и конечного момента грузовой операции, получим уравнение для определения перемещения
центра масс механической системы в процессе грузовой операции должна сохранять свою величину. Приравняв абсциссы центра масс для начального и конечного момента грузовой операции, получим уравнение для определения перемещения  ,
, - абсцисса центра масс судна в начальный момент времени.
- абсцисса центра масс судна в начальный момент времени. .
. .
.