 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Часть 2. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дифференциальные уравнения занимают особое место в математике и имеют многочисленные приложения в большом спектре наук. Исследования природных процессов и изучение закономерностей общественных процессов приводят к построению математических моделей, основой которых являются дифференциальные уравнения. В дифференциальных уравнениях неизвестная функция содержится вместе со своими производными. Основной задачей теории дифференциальных уравнений является изучение функций, представляющих собой решения этих уравнений. В этой части излагаются элементы теории обыкновенных дифференциальных уравнений, когда неизвестные функции зависят от одной переменной. Теория дифференциальных уравнений, когда неизвестные функции зависят от нескольких переменных — уравнения в частных производных, является более сложной и представляет специальный раздел математики.
Глава 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА Основные понятия Базовые определения Определение 1. Уравнение вида
где х — независимая переменная, у и у' — соответственно неизвестная функция и ее производная, называется дифференциальным уравнением первого порядка. Примеры дифференциальных уравнений первого порядка:
В случае когда из уравнения можно выразить у', оно имеет вид
Уравнение (9.1) называется уравнением первого порядка, разрешенным относительно производной. В дальнейшем будем рассматривать уравнения первого порядка именно такого вида. Примеры уравнений, разрешенных относительно производной:
Приведем примеры уравнений, которые можно разрешить относительно производной неизвестной функции у'. Пример 1. (y')2 = x2 + у2, откуда получаем два уравнения первого порядка у' = ±
Определение 2. Решением дифференциального уравнения первого порядка называется функция у = φ(x), определенная на некотором интервале (а, b), которая при подстановке в уравнение обращает его в тождество. Например, функция у = х2 тождественно обращает в нуль левую часть уравнения ху' — 2х2 = 0 и потому представляет собой решение этого уравнения. В теории дифференциальных уравнений основной задачей является вопрос о существовании и единственности решения. Ответ на него дает теорема Коши, которую мы приводим без доказательства. ТЕОРЕМА 1. Пусть дано дифференциальное уравнение (9.1). Если функция f(x,y) и ее частная производная f'y(x,y) непрерывны в некоторой области D плоскости Оху, то в некоторой окрестности любой внутренней точки (x0, у0) этой области существует единственное решение уравнения (9.1), удовлетворяющее условию у = у0 при х = x0.
График решения дифференциального уравнения называется интегральной кривой. В области D содержится бесконечно много интегральных кривых. Теорема Коши гарантирует, что при соблюдении определенных условий через каждую внутреннюю точку области D проходит только одна интегральная кривая. Условия, которые задают значение функции у0 в фиксированной точке x0, называют начальными условиями (условиями Коши) и записывают в такой форме:
Задача нахождения решения уравнения (9.1), удовлетворяющего условию (9.2), называется задачей Коши — из множества интегральных кривых выделяется та, которая проходит через заданную точку (x0, y0) области D. В ряде случаев, когда условия теоремы Коши не выполнены, через некоторые точки плоскости Оху либо не проходит ни одной интегральной кривой, либо проходит более одной интегральной кривой; эти точки называются особыми точками данного дифференциального уравнения. Определение 3. Общим решением уравнения (9.1) называется функция у = φ(x, С), удовлетворяющая этому уравнению при произвольном значении постоянной С. Определение 4. Частным решением уравнения (9.1) в области D называется функция у = φ(х,С0), полученная при определенном значении постоянной С = С0. Общее решение у = φ(x, С) описывает семейство интегральных кривых на плоскости Оху. Условия Коши (9.2) фиксируют произвольную постоянную С и позволяют выбрать из семейства интегральных кривых уравнения (9.1) одну интегральную кривую у = φ(x,C0), проходящую через заданную точку (x0, y0). Например, рассмотрим уравнение у' = 2х. Правая часть этого уравнения удовлетворяет условиям теоремы Коши во всех точках плоскости Оху (функции f(x, у) = 2х и f'y(x, у)
Поиск по сайту: |




 .
.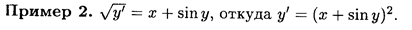

 0 определены и непрерывны на всей плоскости Оху). Нетрудно видеть, что общим решением уравнения является функция у = х2 + С, где С — произвольная постоянная, описывающая семейство парабол (рис. 9.1). Для отыскания частного решения зададим произвольные начальные условия (9.2) и подставим их в формулу общего решения; получаем, что С = у0 — x02, откуда находим частное решение у = х2 + у0 – х02. Это частное решение выделяет из семейства парабол одну, проходящую через точку (х0, у0).
0 определены и непрерывны на всей плоскости Оху). Нетрудно видеть, что общим решением уравнения является функция у = х2 + С, где С — произвольная постоянная, описывающая семейство парабол (рис. 9.1). Для отыскания частного решения зададим произвольные начальные условия (9.2) и подставим их в формулу общего решения; получаем, что С = у0 — x02, откуда находим частное решение у = х2 + у0 – х02. Это частное решение выделяет из семейства парабол одну, проходящую через точку (х0, у0).