 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЛАБОРАТОРНА РОБОТА № 43.3
ВИЗНАЧЕННЯ ПРИВЕДЕНОЇ ДОВЖИНИ ФІЗИЧНОГО МАЯТНИКА
Мета роботи:вивчення законів коливанняфізичного та математичного маятників. Завдання:експериментально та теоретично знайти приведену довжину фізичного маятника. Прилади і обладнання: фізичний маятник, математичний маятник, лінійка, секундомір.
Теоретична частина Фізичний маятник – це тіло, яке може обертатись відносно довільної горизонтальної осі, що не проходить через центр маси. Під дією моменту сили тяжіння mg, плече якої дорівнює a·sinα, тіло обертається навколо точки підвісу О (рис.9.2).a – відстань від точки О обертання (точки підвісу) до точки С - центра маси тіла. Запишемо основне рівняння динаміки обертального руху
I- момент інерції тіла,
При малих кутах α (менших 5о) можна вважити, що sinα = α. Одержуємо Порівнюючи це рівняння із загальним рівнянням незатухаючих гармонічних коливань одержуємо циклічну частоту
Таким чином, період коливань фізичного маятника залежить від положення точки підвісу О і форми тіла, тобто його моменту інерції відносно цієї точки. Для математичного маятника, який уявляє собою матеріальну точку, підвішену на невагомій нерозтяжній нитці довжиною L, момент інерції
Приведеною довжиною Lпр фізичного маятника називається така довжина математичного маятника, період якого дорівнює періоду коливань фізичного маятника. Із (9.5) і (9.6) при
Момент інерції стержня (рис.9.1) з урахуванням теореми Штейнера дорівнює Таким чином, із (9.7) і (9.8) одержуємо теоретичне значення приведеної довжини Теоретичне значення періоду коливань фізичного маятника знаходимо із (9.5) і (9.8) Практична частина
Таблиця 9.1.
12. Розрахувати похибку Lтеор.
Контрольні запитання
1. Що таке фізичний маятник? 2. Що таке математичний маятник? 3. Одержати диференціальне рівняння вільних гармонічних коливань фізичного маятника. 4. Одержати період коливань фізичного маятника. 5. Одержати період коливань математичного маятника. 6. Дати означення приведеної довжини фізичного маятника. 7. Одержати вираз для приведеної довжини фізичного маятника.
Література
1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80. 2. Лапотинський І.Е., Зачек І.Р. Фізика для інженерів.- Львів: Афіша, 2003.-С. 3. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199. 4. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К. LABORATORY WORK № 43.3
Поиск по сайту: |
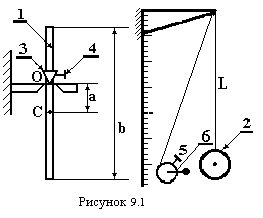 Експериментальна установка (рис.9.1) складається з фізичного 1 та математичного 2 маятників. Опорна призма 3 фізичного маятника може переміщуватись здовж стержня і фіксуватись гвинтом 4. Довжину нитки математичного маятника можна плавно змінювати, намотуючи її на котушку 5 і фіксувати її гвинтом 6.
Експериментальна установка (рис.9.1) складається з фізичного 1 та математичного 2 маятників. Опорна призма 3 фізичного маятника може переміщуватись здовж стержня і фіксуватись гвинтом 4. Довжину нитки математичного маятника можна плавно змінювати, намотуючи її на котушку 5 і фіксувати її гвинтом 6.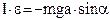 ,(9.1)
,(9.1)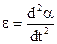 - кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут
- кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут  .Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника
.Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника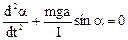 . (9.2)
. (9.2) (9.3)
(9.3)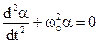 , (9.4)
, (9.4)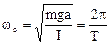 та період коливань фізичного маятника
та період коливань фізичного маятника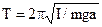 (9.5)
(9.5)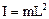 ,
, 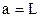 . Отже період коливань математичного маятника залежить тільки від довжини нитки
. Отже період коливань математичного маятника залежить тільки від довжини нитки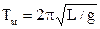 . (9.6)
. (9.6) маємо
маємо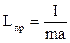 . (9.7)
. (9.7)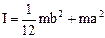 . (9.8)
. (9.8)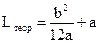 . (9.9)
. (9.9)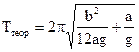 . (9.10)
. (9.10) .
.