 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЛАБОРАТОРНА РОБОТА № 43.1
ФІЗИЧНИЙ МАЯТНИК Мета роботи:вивчення законів коливанняфізичного маятника. Завдання:а) перевірити залежність періоду вільних коливань фі-зичного маятника від його моменту інерції; б) визначити величину прискорення вільного падіння. Прилади і обладнання: фізичний маятник, секундомір, лінійка.
Під час руху маятника світловий потік від лампочки фотоелектричного датчика перекривається, що вмикає електронну схему підрахунку кількості коливань та секундомір. Після натискування вимикача “СТОП” секундомір зупиняється після закінчення поточного повного коливання. Теоретична частина
I- момент інерції тіла,
При малих кутах α (менших 5о) можна вважити, що sin α = α. Одержуємо Порівнюючи одержане рівняння із загальним рівнянням незатухаючих гармонічних коливань одержимо циклічну частоту коливань
Розв’язком рівняння (5.4) є рівняння незатухаючих гармонічних коливань
Момент інерції маятника відносно точки коливання О дорівнює сумі моменту інерції вантажу (матеріальної точки) Iвант = МZ2 і стержня. Враховуючи теорему Штейнера, маємо Iстержня = 1/12 mb2 + m(b/2 – a)2 (рис.5.3). Таким чином момент інерції маятника, як функція відстані Z від точки підвісу до центра вантажу
I = МZ2 + 1/12 mb2 + m(b/2 – a)2 (5.7)
Знайдемо положення точки С центра мас маятника, тобто відстань L як функцію Z. За правилом моментів відносно точки С (рис.5.3) маємо mgZ1 = MgZ2 (5.8)
Із рис.5.3 видно, що L = Z – Z2, і Z1 + b/2 =L + a . (5.9)
Поиск по сайту: |
 Експериментальна установка (рис.5.1) складається із основи 1, вирівнювання якої здійснюється ніжками 2. В основі закріплена стійка 3, на якій фіксується нижній кронштейн 4 з фотоелектричним датчиком 5. На верхньому кронштейні 6 підвішений фізичний маятник. Він складається зі стержня 7, вантажу 8 і фіксатора 9. На стержні 7 через 10мм зроблені кільцеві нарізки для точного визначення довжини маятника та чіткої фіксації вантажу 8. На передній панелі приладу знаходяться: індикатор кількості коливань–10, індикатор часу–14, вимикачі “СЕТЬ”–11 “СБРОС”–12 і “СТОП”–13.
Експериментальна установка (рис.5.1) складається із основи 1, вирівнювання якої здійснюється ніжками 2. В основі закріплена стійка 3, на якій фіксується нижній кронштейн 4 з фотоелектричним датчиком 5. На верхньому кронштейні 6 підвішений фізичний маятник. Він складається зі стержня 7, вантажу 8 і фіксатора 9. На стержні 7 через 10мм зроблені кільцеві нарізки для точного визначення довжини маятника та чіткої фіксації вантажу 8. На передній панелі приладу знаходяться: індикатор кількості коливань–10, індикатор часу–14, вимикачі “СЕТЬ”–11 “СБРОС”–12 і “СТОП”–13. Фізичний маятник – це тіло, яке може обертатись відносно довільної горизонтальної осі, що не проходить через центр маси. Під дією моменту сили тяжіння mg, плече якої дорівнює L·sinα, тіло обертається навколо точки підвісу О (рис.5.2).L – відстань від точки О обертання (точки підвісу) до точки С - центра маси тіла. Записуємо основне рівняння динаміки обертального руху
Фізичний маятник – це тіло, яке може обертатись відносно довільної горизонтальної осі, що не проходить через центр маси. Під дією моменту сили тяжіння mg, плече якої дорівнює L·sinα, тіло обертається навколо точки підвісу О (рис.5.2).L – відстань від точки О обертання (точки підвісу) до точки С - центра маси тіла. Записуємо основне рівняння динаміки обертального руху ,(5.1)
,(5.1)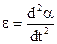 - кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника
- кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника . (5.2)
. (5.2) (5.3)
(5.3)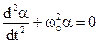 , (5.4)
, (5.4)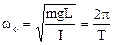 .Період коливань фізичного маятника
.Період коливань фізичного маятника (5.5)
(5.5) (5.6)
(5.6) Для виконання першого пункту завдання необхідно змінювати момент інерції маятника. Це здійснюється шляхом переміщення вантажу 8 вздовж стержня 7 (рис.5.1). Але при цьому змінюється і положення центра маси, тобто відстань L, що також необхідно врахувати.
Для виконання першого пункту завдання необхідно змінювати момент інерції маятника. Це здійснюється шляхом переміщення вантажу 8 вздовж стержня 7 (рис.5.1). Але при цьому змінюється і положення центра маси, тобто відстань L, що також необхідно врахувати.