 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЛАБОРАТОРНА РОБОТА № 43.2
КОЛИВАННЯ СТЕРЖНЯ
Мета роботи: дослідити залежність періоду коливань стержня від відстані між віссю обертання та центром мас. Прилади: стержень, лінійка, секундомір. Завдання роботи:а) побудувати теоретичний та експериментальний графіки залежності періоду коливань стержня б) знайти мінімум функції
Теоретична частина
Коливаннями називають процеси, що повторюються з часом. Таку повторюваність мають, наприклад, рух математичного та фізичного маятників, рух струн музичних інструментів, зміна заряду та напруги на пластинах конденсатора і т. ін. Розглянемо коливання стержня, положення осі якого можна змінювати вздовж стержня. Такий стержень уявляє собою фізичний маятник. Фізичним маятником називають тверде тіло довільної форми, що має можливість обертатись навколо горизонтальної осі під впливом сили тяжіння. Період коливань фізичного маятника визначається за формулою:
де I – момент інерції стержня, m – його маса, а – відстань від осі обертання до центра мас, g – прискорення вільного руху. Момент інерції I у даному випадку визначається за теоремою Штейнера:
де
Після підстановки (7.2) і (7.3) в формулу (7.1) одержуємо:
Проведемо дослідження формули (7.4). Величина а може змінюватись в інтервалі:
2. При 3. Дослідження формули (7.4) на наявність екстремуму показує, що функція має мінімум, координата якого знаходиться з умови:
або приблизно при Для експериментального дослідження залежності періоду коливань стержня від положення осі обертання застосовується пристрій, зображений на рисунку 7.1. Якщо стержень 1 встановити опорною призмою 2 на кронштейн 3, вивести з положення рівноваги на деякий кут
Практична частина 1. Виміряти довжину стержня 2. Встановити опорну призму 2 на першому значенні a з таблиці. 3. Встановити стержень на кронштейн 3. 4. Вивести маятник з положення рівноваги на кут 5. Повторити виміри з іншими значеннями а, які вказані в таблиці 7.1.
Таблиця 7.1
6. За формулою (7.4) розрахувати теоретичні значення періоду T. Порівняти експериментальні та теоретичні значення періоду. 7. На одному полі (бажано на міліметровому папері) побудувати теоретичний та експериментальний графіки
8. Знайти першу похідну функції (7.4) по параметру а. З умови Зробити висновки.
Додатково. Побудувати теоретичний та експериментальний графіки за допомогою комп’ютера. Для більш детального дослідження мінімуму функції (7.4) провести додаткові вимірювання періоду коливань в інтервалі а Контрольні запитання 1. Що таке гармонічні коливання? Записати диференціальне рівняння гармонічних коливань і його рішення. 2. Що так фізичний маятник? Вивести формулу періоду коливань фізичного маятника. 3. Сформулювати теорему Штейнера 4. Вивести формулу періоду коливань стержня.. 5. Намалювати графік залежності періоду коливань стержня від відстані між віссю обертання та центром мас.
Література
1. Сивухин Д. В. Общий курс физики. – т. 1. – М.: Наука, 1980. 2. Савельев И. В. Курс общей физики.– т. 1. – М.: Наука, 1982.
Інструкцію склав доцент каф. фізики ЗНТУ Правда М.І. LABORATORY WORK № 43.2 OSCILLATION OF PEG
Purpose of work is to probe dependence of period of oscillations of peg on distance between the axis of rotation and center of peg. Devices: peg, straightedge, stop-watch. Task of work: 1) to build the theoretical and experimental graph of dependence of period of oscillations T of peg from dimensionless length 2) to find minimum functions
Theoretical part
Will consider oscillation of peg, position of axis of which, it is possible to change along a peg. Such peg shows by itself a physical pendulum. The period of oscillation of the physical pendulum is determined by formula
Where I is a moment of inertia of peg, m is mass, a is distance from the axis of rotation to the center of the masses, g is the free fall acceleration. The moment of inertia I in this case is determined on the theorem of Steiner:
where I0 is a moment of inertia of peg in relation to an axis which go athwart to the peg through his center:
After a substitution (8.2) and (8.3) in a formula (8.1) get:
In the formula (8.4) the size a can change in the interval: 1. At 2. At
Figure 8.1
3. Research of formula (8.4) shows on the extremum, that a function has minimum, a coordinate of which is from a condition
or approximately at For experimental research of dependence of period of oscillations of peg from position of axis of rotation a device, represented on fig. 8.1, is used. If peg 1 to set a supporting prism 2 on a bracket 3, to show out of position of equilibrium on some corner
Practical part
1. Measure length of peg - l. 2. Set a supporting prism 2 on the first value from a table. 3. Set a peg on a bracket 3. 4. Show a pendulum out of position of equilibrium on a corner 5. Repeat measurings with other the values a which are indicated in a table 8.1.
Table 8.1
6. After a formula (8.4) to expect the theoretical values of period of T. To compare the experimental and theoretical values of period. 7. On one field (it is desirable on a plotting paper) to build theoretical and experimental graph 8. Find the first derivative of function (8.4) on a parameter . From a condition Draw conclusion.
Figure 8.2
Additionally. To build theoretical and experimental graph by a computer. For more detailed research of a minimum of function (8.4) do the additional measurings of period of oscillations in an interval with a less step (for example -
Control questions
1. What harmonic oscillations? Write down differential equalization of harmonic oscillations and his decision. 2. What is physical pendulum? Write down the formula of the period of oscillation of the physical pendulum. 3. Formulate the theorem of Steiner. 4. Draw the graph of the dependence of period of oscillations of peg from distance between the axis of rotation and pegycenter.
Literature
1. Сивухин Д. В. Общий курс физики. – т. 1. – М.: Наука, 1980. 2. Савельев И. В. Курс общей физики.– т. 1. – М.: Наука, 1982.
Authors: M.I. Pravda, the reader, candidate of physical and mathematical sciences. Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
Поиск по сайту: |
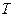 від безрозмірної довжини
від безрозмірної довжини  :
:  ;
; експериментальним та теоретичним шляхом.
експериментальним та теоретичним шляхом. , (7.1)
, (7.1)
 , (7.2)
, (7.2) – момент інерції стержня відносно осі, що проходить перпендикулярно до стержня через його центр:
– момент інерції стержня відносно осі, що проходить перпендикулярно до стержня через його центр: (7.3).
(7.3). (7.4).
(7.4). .
. 1. При
1. При  , період
, період  , тобто при закріпленні стержня в центрі мас він взагалі не буде коливатись, оскільки в цьому випадку сумарний момент сил тяжіння, що діють на стержень у будь-якому його положенні, дорівнюватиме нулю.
, тобто при закріпленні стержня в центрі мас він взагалі не буде коливатись, оскільки в цьому випадку сумарний момент сил тяжіння, що діють на стержень у будь-якому його положенні, дорівнюватиме нулю. для Т одержуємо:
для Т одержуємо: 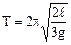 (7.5)
(7.5) . Після диференціювання (7.4) знаходимо, що функція має мінімум при
. Після диференціювання (7.4) знаходимо, що функція має мінімум при , (7.6)
, (7.6) .
. і відпустити, то він буде здійснювати коливання відносно положення рівноваги.
і відпустити, то він буде здійснювати коливання відносно положення рівноваги. .
.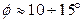 і відпустити; виміряти час 10 повних коливань. Період Т занести в таблицю 7.1.
і відпустити; виміряти час 10 повних коливань. Період Т занести в таблицю 7.1.
 , см
, см
 за зразком, який представлено на рис.7.2.
за зразком, який представлено на рис.7.2.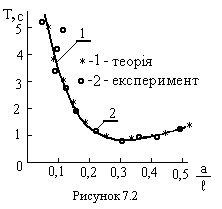
 знайти теоретичне значення координати мінімуму функції; порівняти теоретичне значення з експериментальним, знайденим по графіку.
знайти теоретичне значення координати мінімуму функції; порівняти теоретичне значення з експериментальним, знайденим по графіку. з меншим кроком (наприклад
з меншим кроком (наприклад  ). Розрахувати теоретичні значення періоду при тих самих значеннях
). Розрахувати теоретичні значення періоду при тих самих значеннях  . Порівняти теорію з експериментом, побудувавши графіки. Зробити висновки, щодо справедливості формул (7.1) – (7.4).
. Порівняти теорію з експериментом, побудувавши графіки. Зробити висновки, щодо справедливості формул (7.1) – (7.4).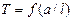 by an experimental and theoretical way.
by an experimental and theoretical way. , (8.1)
, (8.1) , (8.2)
, (8.2)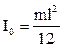 (8.3)
(8.3)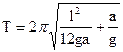 (8.4)
(8.4) .
. for T get:
for T get: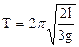 (8.5).
(8.5).
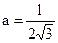 , (8.6)
, (8.6) .
. and to release; to measure time 10 full oscillations. Write down the period of T to the table 8.1.
and to release; to measure time 10 full oscillations. Write down the period of T to the table 8.1. /l
/l
 , cm
, cm
 according to sample, which is presented on fig. 8.2.
according to sample, which is presented on fig. 8.2. to find the theoretical value of co-ordinate of a minimum of function; to compare a theoretical value to experimental, found for graphic
to find the theoretical value of co-ordinate of a minimum of function; to compare a theoretical value to experimental, found for graphic 
 ). Expect the theoretical values of period at those values. Compare a theory to the experiment, building graphic arts. Draw conclusion, in relation to justice of formulas (8.1) – (8.4).
). Expect the theoretical values of period at those values. Compare a theory to the experiment, building graphic arts. Draw conclusion, in relation to justice of formulas (8.1) – (8.4).