 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Із (1.5) і (1.6) отримуємо період коливань пружинного маятника
Коли на пружині висить тягарець, який не здійснює коливань, він деформує пружину на величину хо. За законом Гука F = mg = kxo , можна знайти жорсткість пружини Тоді формула (1.8)для періоду коливань набуває виду
Таким чином, експериментально вимірюючи період коливань Т і видовження пружини хо,від її недеформованого стану до положення рівноваги при різних навантаженнях, можна по куту нахилу графіка Т2 = f(xo) (див. формулу 1.11) знайти прискорення вільного падіння. Так виконується перше завдання. Друге завдання роботи виконується на основі формули (1.8), тобто перевіряється лінійність залежності Практична частина 1. Зняти з пружини державку тягарців і відмітити по лінійці положення кінця пружини (точки підвісу державки). 2. Підвісити державку і, комбінуючи набором тягарців, змінювати загальну масу mпружинного маятника від найменшої (одна державка) до найбільшої (підвішені усі тягарці). Маса державки 11 г, маси тягарців вказані на них. 3. З вибраною масою m виміряти деформацію хопружини до положення рівноваги, а потім, надавши невеликої амплітуди (2÷3 см), виміряти секундоміром час 20 коливань. Результати вимірів занести в таблицю 1.1. Кількість комбінацій мас повинна бути не меншою 9÷10. Таблиця 1.1
4. За результатами кожного досліду розрахувати жорсткість пружини k за формулою (1.9) і знайти її середнє значення. 5. Побудувати графіки: 1) Т2 = f(xo); 2) На прямолінійних частинах графіків (рис.1.3) вибрати по дві точки 1-2 і 3-4, визначити їх координати по маштабованим осям, але не із таблиці, і за формулами (1.12) та (1.13) розрахувати g і k.
 (1.12) (1.12) 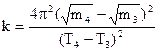 (1.13) (1.13)
6. Зробити висновок, порівнявши значення g з табличним, а k, одержане за формулою (1.13), з середнім значенням, знайденим за формулою (1.9). У висновку також відмітити чи лінійні графіки одержано у дослідах і якщо так, то про що це свідчить? Контрольні запитання 1. Що таке коливання? 2. Які коливання називаються гармонічними? 3. Дати визначення параметрів гармонічних коливань. 4. Одержати диференціальне рівняння незатухаючого гармонічного коливання для пружинного маятника. 5. Розв’язати диференціальне рівняння незатухаючих коливань. 6. Записати вирази для зміщення, швидкості і прискорення при незатухаючих гармонічних коливаннях та намалювати їх графіки. 7. Одержати формулу періоду незатухаючих коливань пружинного маятника. Література 1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80. 2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.195-196. 3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Інструкцію склав доцент кафедри фізики ЗНТУ Манько В.К. Laboratory work № 41 SPRING PENDULUM
Purpose of the work is to study dependence of period of oscillations on mass for a spring pendulum. Task:to define acceleration offree falling; experimentally to check up the theoretical formula of period of the spring pendulum.
Theory Oscillations of a spring pendulum are acted upon by the elastic force
where x is a deviation from state of stable equilibrium, k is a rigidity of the spring. The period of oscillations is
where m is mass of the body fixed on the spring. Spring pendulum (fig.2.1) it a body is suspended on a spring. At the leadingout of it from position of equilibrium of xo on distance of x there is force of elasticity F, which by Hook`s law is evened F = -kx, where k is rigidity of spring. This force gives the acceleration
Equation (2.1) can be write down in such a way
Designating Equation (2.3) is named differential equation of undamped free harmonic oscillations. The decision of this equation is a harmonic function
what sets the coordinate of x load in any moment of time t. Will consider descriptions of harmonic oscillations. Amplitude of Ao is most deviation of point from position of equilibrium Cyclic frequency of oscillations it is an amount of oscillations for 2π seconds. Period of oscillations it is time of one full-oscillate, or time for which the phase of oscillation changes on 2π. Frequency of oscillations it is an amount of oscillations for 1 second.
Поиск по сайту: |
 . (1.8)
. (1.8) . (1.9)
. (1.9) (1.10), або
(1.10), або  . (1.11)
. (1.11)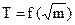 .
.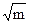 кг0,5
кг0,5
 Н/м
Н/м
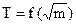

 , (2.1)
, (2.1)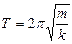 , (2.2)
, (2.2) , or
, or 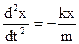 . (2.3)
. (2.3)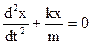 . (2.4)
. (2.4)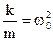 , get
, get  . (2.5)
. (2.5) , or
, or 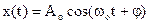 (2.6)
(2.6)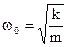 – (2.7)
– (2.7) – (2.8)
– (2.8)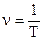 – (2.9)
– (2.9)