 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
DETERMINATION OF THE RESULTED LENGTH OF PHYSICAL PENDULUM
Purpose of work: study of laws of oscillation physical and mathematical pendulums. Task: experimentally and theoretically to find resulted length of physical pendulum. Devices and equipments: physical pendulum, mathematical pendulum, straightedge, stop-watch. The experimental setting (fig.10.1) consists of physical 1 and mathematical 2 pendulums.
Figure 10.1
Length of mathematical pendulum can be fluently changed, reeling it in 5 and to fix spirally 6.
Theoretical part
A physical pendulum is a body which can be revolved relatively of arbitrary horizontal axis, that not go through the center of mass. Under the action of moment of force mg, the arm of which is L·sinα, a body is revolved round the point of hang up O (fig.10.2). L is distance from a point O rotation (points of hang up) to the point of C - center of mass of body. Write down the fundamental equation of the rotational motion dynamics
Figure 10.2
Thus, get differential equation of undamped oscillation of the physical pendulum
At small corners α (less 5о) is it possible, that sin α = α. Get
get cyclic frequency
Thus, the period of oscillation of the physical pendulum depends on position of point of hang up O and forms of body, that to its moment of inertia in relation to this point. For a mathematical pendulum, which is a material point, suspended on a weightless unstretching thread long L, moment of inertia is
The resulted length of Lres of physical pendulum is such length of mathematical pendulum the period oscillation of which equals the period of oscillation of the physical pendulum. From (10.5) and (10.6) we have
A moment of inertia of peg (fig.10.1) is taking into account a theorem Steiner Thus, from (10.7) and (10.8) get the theoretical value of the resulted length
Find the theoretical value of period of oscillation of the physical pendulum from (10.5) and (10.8)
Practical part
Table 10.1
12. Expect the error of Ltheory.
Control questions
8. What is physical pendulum? 9. What is mathematical pendulum? 10. Get differential equation of free harmonic oscillation of the physical pendulum. 11. Get the period of oscillation of the physical pendulum. 12. Get the period of oscillation of the mathematical pendulum. 13. Give determination of the resulted length of physical pendulum. 14. Get expression for the resulted length of physical pendulum.
Literature
1 Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80. 2. Лапотинський І.Е., Зачек І.Р. Фізика для інженерів.- Львів: Афіша, 2003.-С. 3. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199. 4. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences. Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
Поиск по сайту: |

 , (10.1) I is a moment of inertia of body,
, (10.1) I is a moment of inertia of body, 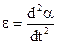 is angular acceleration. A sign does minus take into account, that the moment of force of mg is diminished by a corner α.
is angular acceleration. A sign does minus take into account, that the moment of force of mg is diminished by a corner α.
 . (10.2)
. (10.2) (10.3) Comparing this equation to general equation of undamped harmonic oscillations
(10.3) Comparing this equation to general equation of undamped harmonic oscillations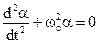 , (10.4)
, (10.4) and period of oscillation of the physical pendulum
and period of oscillation of the physical pendulum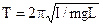 (10.5)
(10.5)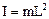 ,
, 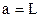 . Consequently the period of oscillation of the mathematical pendulum depends only on length of thread
. Consequently the period of oscillation of the mathematical pendulum depends only on length of thread . (10.6)
. (10.6) . (10.7)
. (10.7)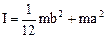 . (10.8)
. (10.8)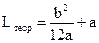 . (10.9)
. (10.9) . (10.10)
. (10.10) .
.