 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЛАБОРАТОРНА РОБОТА № 42
МАТЕМАТИЧНИЙ МАЯТНИК
Мета роботи: вивчення законів коливання математичного маятни- ка. Завдання: а) перевірити залежність періоду вільних коливань ма- тематичного маятника від довжини нитки; б) визначити прискорення вільного падіння. Прилади і обладнання:математичний маятник, секундомір, лі- нійка.
Теоретична частина
Математичний маятник – це тіло масою m, яке можна вважати матеріальною точкою, підвішене на невагомій нерозтягуваній нитці. Знайдемо період коливань такого маятника. Якщо нитку відхилити від вертикального положення, виникає зворотний момент сили тяжіння mg, плече якої дорівнює L·sinα (рис.3.2). Під дією цього моменту тіло m обертається навколо точки підвісу О. Записуємо основне рівняння динаміки обертального руху
Тут: Одержуємо диференціальне рівняння незатухаючих коливань математичного маятника
При малих кутах α (менших 5о) можна вважити, що sinα = α. Одержуємо Порівнюючи це рівняння із загальним рівнянням незатухаючих гармонічних коливань маємо
Піднесемо це рівняння до квадрату
Видно, що залежність квадрату періоду Т2 від зміни довжини нитки ΔL за теорією повинна бути лінійною, а її нахил визначається прискоренням вільного падіння g. Розв’язком рівняння (3.4) є рівняння незатухаючих гармонічних коливань
Практична частина 1. Відпустити стопорний гвинт 5 і встановити довжину нитки приблизно 50 см. 2. Привести маятник у коливальний рух, відхиливши його на кут не більший, ніж 5о. 3. В одному з крайніх положень маятника, який коливається, увімкнути секундомір і виміряти час 20 повних коливань. Результат записати в таблицю 3.1. Це відповідатиме значенню ΔL = 0.
Таблиця 3.1
4. Замітити положення бусинки 2 по лінійці 7. Відпустити стопорний гвинт 6 і подовжити нитку на ΔL = 10 см. Подовження нитки вимірювати по переміщенню разом з нею бусинки. Закрутити стопорний гвинт. 5. Повторювати п. 2 - 5 до максимально можливої довжини нитки (до підлоги). Коли бусинка опуститься нижче лінійки, перемістити її вгору. 6. Розрахувати період Т = t/20 та його квадрат. Результат занести в таблицю 3.1. 7. 8. На прямолінійній частині графіка вибрати дві точки 1 і 2, ви 9. значити їх координати
10. Порівняти одержане значення з табличним 9,8 м/с2. Зробити висновок.
Контрольні запитання 1. Що таке математичний маятник? 2. Складіть та запишіть диференціальне рівняння вільних гармонічних коливань математичного маятника. 3. Запишіть рівняння коливань, яке є рішенням диференціального рівняння математичного маятника. Накресліть графік цього рівняння. 4. Дати визначення величинам, які входять у рівняння коливань математичного маятника. 5. Записати формули для періоду та циклічної частоти коливань математичного маятника.
Література
1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80. 2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.195-196. 3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К. Laboratory work № 42 MATHEMATICAL PENDULUM
Purpose of work: to measure the free fall acceleration. INSTRUMENTATION AND APPLIANCES: mathematical pendulum; the stop-watch, straightedge.
Short theory
The point mass suspended by means of an unelastic weightless thread is called the mathematical pendulum. The restoring force is the projection of the force of gravity P=mg on the direction of motion of the point mass. In this case
where a = x/l, the angle between positions of l in free state and deviation state.
Figure 4.1
If the angles a are so small that sina » a, then Since this force is always directed to the equilibrium position and that is why it has a sign opposite to that of x: In this case the oscillations are harmonic. The second Newton’s law is Finally we obtain the differential equation of harmonic oscillations: If g/l=w2, then
Solution of this equation is The cyclic frequency is
and period is equal
i. e., the frequency and the period of oscillations do not depend on the mass of the oscillating body; they are determined only by the length of the thread and the free fall acceleration. The measurement of the period of a mathematical pendulum is used for determine g:
Experimental part
1. Fix the end of the cord in the first position (l = 50 cm). Make the pendulum vibrate (the amplitude of vibration must not be more than the ball diameter). Determine time of 50 oscillations by the stop-watch three times and calculate the period T using the average value of the time. 2. Determine the free fall acceleration g. 3. Calculate an error. 4. Investigate relation between the period T and the length l. Put the end of the cord in the second position (l = 150 cm). Calculate period of oscillations 5. Increase the amplitude of oscillations twice. Test independence of the period on the amplitude of oscillations (small amplitude and big amplitude). 6. Make conclusions.
Control questions 1. What is a mathematical pendulum? 2. What kind of oscillations is called harmonic? 3. Write the differential equation of harmonic oscillations. 4. Write the dependence of deviation upon time for harmonic oscillations. Show this dependence in figure. 5. Give definitions for a period, an amplitude, a frequency, a cyclic frequency and a phase of vibration.
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences. Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
Поиск по сайту: |
 Експериментальна установка (рис.3.1) складається з кронштейна 1, через який перекинута нитка 3, на одному кінці якої прив’язана масивна куля 4, а другий кінець закріплений на котушці 5. Гумова бусинка 2 може переміщуватись по нитці і слугує для вимірювання зміни її довжини, коли куля 3 опуститься нижче лінійки 7. Довжина L нитки змінюється шляхом намотування її на котушку 5, яка фіксується стопорним гвинтом 6. Зміна довжини нитки вимірюється лінійкою 7.
Експериментальна установка (рис.3.1) складається з кронштейна 1, через який перекинута нитка 3, на одному кінці якої прив’язана масивна куля 4, а другий кінець закріплений на котушці 5. Гумова бусинка 2 може переміщуватись по нитці і слугує для вимірювання зміни її довжини, коли куля 3 опуститься нижче лінійки 7. Довжина L нитки змінюється шляхом намотування її на котушку 5, яка фіксується стопорним гвинтом 6. Зміна довжини нитки вимірюється лінійкою 7.
 . (3.1)
. (3.1) - момент інерції матеріальної точки,
- момент інерції матеріальної точки, 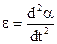 кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.
кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α. . (3.2)
. (3.2) . (3.3)
. (3.3) , (3.4)
, (3.4)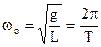 - циклічна частота коливань, Т – період коливань математичного маятника. Прийнявши L = L0 + ΔL, одержуємо
- циклічна частота коливань, Т – період коливань математичного маятника. Прийнявши L = L0 + ΔL, одержуємо . (3.5)
. (3.5) . (3.6)
. (3.6) . (3.7)
. (3.7) Побудувати графік залежності квадрата періоду Т2 від подовження нитки ΔL(рис.3.3). Лінійний вид цього графіка свідчить про справедливість залежності (3.5) Т ~
Побудувати графік залежності квадрата періоду Т2 від подовження нитки ΔL(рис.3.3). Лінійний вид цього графіка свідчить про справедливість залежності (3.5) Т ~  .
.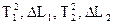 . Знайти прискорення вільного падіння за формулою:
. Знайти прискорення вільного падіння за формулою: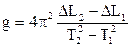 . (3.8)
. (3.8) ,
,
 .
.
 .
. .
. .
.
 ,
, ,
, .
. in the same way and compare with T.
in the same way and compare with T.