 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическая формулировка процессов переноса в сплошной среде
Основная система уравнений гидромеханики имеет вид
Система (1) справедлива для любых жидкостей и газов, но в данном виде не несет информации о свойствах СС. Свойства среды должны задаваться выражениями для тензора напряжений ( Как было сказано выше, для ньютоновской среды имеем реологическое уравнение –– закон линейной связи между тензором напряжений и тензором скоростей деформаций - обобщенный закон Ньютона:
Или в общей форме модель вязкой жидкости
(3) – реологическое уравнение ньютоновской несжимаемой вязкой жидкости. Определение. Вязкая среда несжимаема, если для нее div 1.1. Понятие о газообразных средах. Определение. Вязкая теплопроводная сжимаемая СС - газ, если в ней возмущения распространяются с конечной скоростью распространения звука, Так, в изотермической среде
В адиабатической среде – пренебрегая отводом тепла при распространении звука –
Когда газ – совершенный:
Замечание. Скорость распространения звука в совершенном газе зависит лишь от абсолютной температуры и от физических свойств газа. Газ – агрегатное существование вещества. Реальный газ (РГ) - это газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия. Для описания свойств РГ применяют различные уравнения состояния, отличные от уравнения Клапейрона-Менделеева ( Общая запись модели РГ - Уравнение Ван-дер-Ваальса состояния РГ
где Уравнение состояния Бертло
Здесь постоянные а, b связаны с параметрами критического состояния: pk, V0k, Tk .
Уравнение состояния Вукаловича-Новикова
где B1, B2, … - вириальные коэффициенты сложного вида, вычисление которых проводится с учетом ассоциации молекул – объединения под влиянием Ван-дер-Ваальсовых сил притяжения. 1.2. Простейшие модели материальных сред. Существуют процессы, в которых необходимо учитывать малые изменения плотности жидкости. В этих условиях используют модель упругой жидкости
где Если ввести модуль упругости K=1/β, то (1) имеет вид
Модель с тепловым расширением жидкости(ТР) учитывает: при нагревании - среды расширяются, при охлаждении – сжимаются. Здесь ρ=ρ(T):
где Модель с барическим и тепловым расширением ρ=ρ(p,T):
Модель неньютоновских жидкостей. Так, жидкости, моделируемые условием
Пример. Модель степенной жидкости Оствальда
Здесь связь между τ в слоях жидкости степенная Кажущаяся вязкость в среде –
где k, n – коэффициенты в среде. Определение. Если n<1, то жидкости называются псевдопластичными (сюда относятся суспензии, вязкие жидкости с взвесью мелких частиц). При n>1 – среды – дилатантные (например, крахмальный клейстер). Пример. Вязко-пластическая среда с предельным напряжением сдвига; модель “жидкости” Шведова-Бингама (сюда относятся высокопарафинистые и застывающие нефти, глинистые растворы, лаки, краски):
Физический смысл (6). Пока τ не превышает по mod некоторую предельную величину τ0 (является предельным напряжением сдвига), течение такой среды не начинается (в этом случае
Поиск по сайту: |
 . (1)
. (1) ) и вектора теплового потока (
) и вектора теплового потока (  ). Рассмотрим наиболее употребительные модели тензора напряжений и вектора теплового потока. В выражения для
). Рассмотрим наиболее употребительные модели тензора напряжений и вектора теплового потока. В выражения для  . (2)
. (2) . (3)
. (3) =0, ρ=const, тогда
=0, ρ=const, тогда  - скорость звука равна бесконечности (∞).
- скорость звука равна бесконечности (∞). ,
,  . (6)
. (6) . (7)
. (7) . (8)
. (8) ).
). , где
, где  - коэффициент сверхсжимаемости, функуция от
- коэффициент сверхсжимаемости, функуция от  .
. ,
,  (9)
(9) - внутреннее давление, обусловленное силами притяжения молекул, b - поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами.
- внутреннее давление, обусловленное силами притяжения молекул, b - поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами. . (10)
. (10) , (11)
, (11) , (1)
, (1) - коэффициент сжимаемости:
- коэффициент сжимаемости:  , где p0 – нормальное давление.
, где p0 – нормальное давление.
 , (2)
, (2) - коэффициент объемного расширения; ρ0, T0 – плотность, температура в нормальных условиях.
- коэффициент объемного расширения; ρ0, T0 – плотность, температура в нормальных условиях. . (3)
. (3) - называются ньютоновскими вязкими жидкостями. Существуют среды, в которых связь τ=f(
- называются ньютоновскими вязкими жидкостями. Существуют среды, в которых связь τ=f(  ) – нелинейная (здесь
) – нелинейная (здесь  ). Это неньютоновские среды.
). Это неньютоновские среды.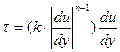 . (4)
. (4) , (5)
, (5)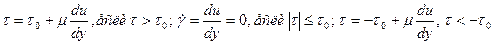 . (6)
. (6) , при этом
, при этом  .
.