 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коэффициенты переноса в рамках статистической теории вязких многокомпонентных инертных и химически реагирующих сред
3.1. Некоторые сведения формальной кинетики химических реакций Процессы химического взаимодействия между компонентами газовой смеси являются следствием неупругих соударений реагирующих частиц. Число таких столкновений пропорционально концентрациям частиц. Привлечение необходимых данных феноменологической теории кинетических процессов позволяет получить замкнутые модели, используемые для описания явлений переноса в химически активных средах. В формальном описании кинетики химических превращений скорость реакций представляется определенной функцией давления, компонент смеси и температуры. Каждая химическая реакция протекает по закону постоянных кратных соотношений, т. е. одно вещество соединяется с другим в строго определенных количествах. Эти количества регламентируются стехиометрическим уравнением. Для обратимой реакции оно представляется в следующем виде:
Здесь Основу описания кинетики составляет закон действующих масс, согласно которому скорость образования продуктов реакции пропорциональна произведению концентраций реагирующих компонент в степени, равной соответствующим стехиометрическим коэффициентам. Если nα считать концентрацией реагента в.молях на единицу объема, то общая скорость образования α-компоненты в r-й реакции будет
а результирующая скорость образования α-компоненты представляется следующим образом:
При химическом равновесии не происходит изменения в составе смеси, т. е. скорости прямой и обратной реакций равны;
Здесь е отвечает равновесным значениям характеристик течения; Относительно простым представляется решение вопроса определения константы скорости реакции, если следовать данным Аррениуса. Теория столкновений (теория Аррениуса) как часть формальной кинетики дает лишь качественное описание результата взаимодействия частиц. Согласно Аррениусу, всякая реакция идет через стадию образования активных (с достаточным запасом энергии) молекул. Экспериментальные исследования показали, что константа скорости реакции непосредственно связана с числом столкновений активных молекул. Ее величина пропорциональна больцмановскому фактору eхр(—ЕIRT), где Е — энергия активации. В связи с этим температурная зависимость для константы скорости реакции имеет вид
где K0 и Е - постоянные в достаточно широком температурном диапазоне. Данная зависимость хорошо предсказывается теорией, основанной на допущении о равновесном распределении реагирующих молекул (атомов). 3.2. Переносные свойства реагирующих многокомпонентных систем Использование молекулярной теории представляется наиболее рациональным подходом при изучении течений реагирующих сред. Это подтверждается тем обстоятельством, что данный метод позволяет должным образом ввести в уравнения течения члены, учитывающие химические реакции. 3.2.1. Коэффиииент вязкости. Согласно строгой теории механики неоднородных газов коэффициент вязкости смеси определяется в виде сложного отношения определителей N-го порядка, элементы которых зависят от температуры, концентраций и вязкостен отдельных компонентов. Для чистых газов в первом приближении вязкость определяется следующим образом:
где T*- характеристическая температура, Широкое применение при расчетах коэффициентов вязкости многокомпонентных газов получила зависимость Уилки:
где μi - коэффициент динамической вязкости /-компоненты, определенный по (1); хк мольная концентрация к-компоненты:
где сi - относительная массовая концентрация i-компоненты; Gik - функция, выражаемая равенством:
Заметим, что в случае бинарной смеси соотношение (2) упрощается и принимает вид
Заметим, что формула (2) является приближением более сложного выражения для вязкости смеси, которое дается теорией Чепмена — Энского. Согласно Уилке, зависимость (2) находится в хорошем соответствии с многочисленными экспериментальными данными в широком диапазоне изменения температур (до 15000 К). 3.2.2. Коэффициент бинарной диффузии. Часто при моделировании диффузионного потока в многокомпонентных системах придерживаются подхода, представляющего исходную смесь бинарной. Некоторая ошибка, получающаяся в определении диффузионного потока, в ряде случаев несущественна. В общем же коэффициенты диффузии отдельных компонент смеси сложным образом зависят от состава смеси и коэффициентов бинарной диффузии Dij всех пар соединений в смеси. Если воспользоваться анализом термохимических явлений и переносных свойств в смесях газов, то вид коэффициента бинарной диффузии Dij для потенциала межмолекулярного взаимодействия Леннарда — Джонса в соответствии с первым приближением теории Чепмена — Энского будет следующий:
где [Dij] ~ см2/с; р — давление, Н/м2; 3.2.3. Интегралы столкновений. Потенциал Леннарда — Джонсона содержит члены, выражающие притяжение и отталкивание молекул, и описывает поведение взаимодействующих частиц на большом и малом расстояниях между ними. Функциональная форма потенциала:
содержит параметры, отличающиеся для различных пар веществ. Подробная информация о значениях σi, σij, εi, εij для широкого крута веществ имеется в справочной литературе. Приближенно σij, εij можно определить по следующим соотношениям: σij=(σi+σj)/2, εij=(εiεj)0.5. Интегралы столкновений (
Погрешность зависимостей (6) не превышает 5 % в диапазоне температур Т = 300 ÷3000 К. 3.2.4. Коэффициент теплопроводности. Для вычисления плотности потока энергии необходимо знать коэффициент теплопроводности. Выражение для коэффициента теплопроводности одноатомного газа по теории Чепмена — Энского следующее:
где [λ]—кал/(см•с•град); μi - определяется по (1); Ř — универсальная газовая постоянная; Мi— молекулярный вес i-компоненты. Согласно строгой кинетической теории газов коэффициент теплопроводности смеси, как и динамический коэффициент вязкости, выражается через определители N-гo порядка, зависящие от коэффициента теплопроводности чистых газов, состава и температуры смеси. Для смеси одноатомных газов удобно употреблять формулу Мейсона и Саксены:
где λi определяется по (7), поправочные функции Glk — по (3). Позднее Мейсон показал, что формула (8) дает результаты, удовлетворительно согласующиеся с данными (отличие не более 8 %) для бинарных газов в диапазоне температур от 1000 до 15000 К, полученными на основе существенно более сложных формул теории Чепмена — Энского. Кроме этого, часто отмечается, что формула для коэффициента теплопроводности смеси одноатомных газов (8) может быть модифицирована путем использования поправочного множителя Эйкена:
Здесь
λ определяется по зависимостям (7). Величины сpi и R в соотношении (9) являются коэффициентом удельной изобарной теплоемкости i-компоненты и газовой постоянной /-компоненты соответственно. Формулы Мейсона, Саксены (8), (10) показали очень хорошие результаты при сравнении с экспериментально определенными коэффициентами теплопроводности большого разнообразия смесей газов в широком (до 15000 К) диапазоне температур. Все это подтверждает идею применения зависимости (10) вместо усложненного соотношения для λпо теории Чемпена — Энского.
Поиск по сайту: |
 . (1)
. (1) —химические символы исходных реагирующих веществ и продуктов реакции соответственно;
—химические символы исходных реагирующих веществ и продуктов реакции соответственно;  — стехиометрические коэффициенты реагентов и продуктов соответственно; N — общее число реагирующих компонент; r — номер реакции; l — число реакций;
— стехиометрические коэффициенты реагентов и продуктов соответственно; N — общее число реагирующих компонент; r — номер реакции; l — число реакций;  — константы скоростей прямой и обратной реакций, зависящие от температуры.
— константы скоростей прямой и обратной реакций, зависящие от температуры. (2)
(2) . (3)
. (3) .В этом случае константа равновесия Кп определяется как отношение констант скоростей прямой и обратной реакций. В химической кинетике наряду с константой равновесия, выраженной через число молей, широко пользуются константами равновесия, выраженными через парциальные давления КР, мольные концентрации Кх, относительные массовые концентрации Кс. Между ними имеются связи:
.В этом случае константа равновесия Кп определяется как отношение констант скоростей прямой и обратной реакций. В химической кинетике наряду с константой равновесия, выраженной через число молей, широко пользуются константами равновесия, выраженными через парциальные давления КР, мольные концентрации Кх, относительные массовые концентрации Кс. Между ними имеются связи: . (4)
. (4)
 (5)
(5) , (1)
, (1) , Mi – молекулярная масса i-компоненты, σi – диаметр столкновений,
, Mi – молекулярная масса i-компоненты, σi – диаметр столкновений, - интеграл соударений для переноса импульса, выражающий меру отклонения от модели, которая рассматривает молекулы газа как твердые шары и для которой
- интеграл соударений для переноса импульса, выражающий меру отклонения от модели, которая рассматривает молекулы газа как твердые шары и для которой  .
. (2)
(2) ,
, . (3)
. (3) . (4)
. (4)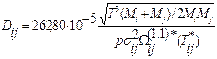 , (5)
, (5) - интеграл соударений для переноса масс, выражающий меру отклонения от модели, рассматривающей молекулы газа как твердые шары, для которой
- интеграл соударений для переноса масс, выражающий меру отклонения от модели, рассматривающей молекулы газа как твердые шары, для которой  =l;
=l;  Т* — характеристическая температура; εij/к - параметр потенциальной энергии молекул, характеризующий взаимодействие молекул i-го и j-го сортов; σij — эффективный диаметр столкновений молекул.
Т* — характеристическая температура; εij/к - параметр потенциальной энергии молекул, характеризующий взаимодействие молекул i-го и j-го сортов; σij — эффективный диаметр столкновений молекул.
 . (6)
. (6) , (7)
, (7) (8)
(8) ; (9)
; (9) (10)
(10)
 . (11)
. (11)