|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Глава 7. Статика жидкостей и их свойства. Основные законы равновесия
1. Уравнения равновесия жидкости и газа Как отмечалось выше, в гидростатике рассматриваются законы равновесия жидкости (газа), находящейся в покое. Если жидкость (газ) находится в состоянии покоя относительно стенок сосуда, в котором она заключена, а сосуд покоится или движется с постоянной скоростью относительно земли, то покой называется абсолютным. Если жидкость покоится относительно стенок сосуда, а сосуд движется относительно земли с ускорением, то покой называется относительным. Движение жидкости в случае относительного покоя можно рассматривать как переносное. Из приведенных определений вытекает, что в случае абсолютного покоя на жидкость действует сила тяжести, а в случае относительного покоя - сила тяжести и сила инерции переносного движения. Так как в покоящейся жидкости скорости деформации εik=0, то из реологического уравнения для вязкой жидкости (см.выше реологический закон) имеем
то есть в покоящейся жидкости действуют только нормальные сжимающие напряжения. Зам.: По Л. Прандтлю «жидкостью называется такое тело, в котором в состоянии равновесия всякое сопротивление деформации равно нулю». Из этого определения следует, что Величина этих напряжений не зависит от направления и равна давлению. Это давление называется гидростатическим. Подставив соотношения (1) в уравнения движения сплошной среды в напряжениях, получим (
Уравнения (2) называются уравнениями Эйлера в гидростатике. Умножив скалярно векторное уравнение (2) на единичный вектор
то есть изменение давления в каком-либо направлении Умножим скалярные уравнения (2) на dxj. Так как при равновесии p=p(xi), то
Поверхности, вдоль которых р = соnst, называются изобарами. Из равенств (4) следует, что уравнение изобары имеет вид
где вектор dr лежит в плоскости, касательной к изобаре. Тогда из (5) вытекает, что напряжение массовой силы направлено по нормали к изобаре. Этот же вывод следует непосредственно из равенств (2).
Очевидно, что уравнения (2)-(5) в равной мере справедливы как для сжимаемых, так и для несжимаемых жидкостей. Из уравнений (4) имеем, что
где М0, М -точки, в которых гидростатическое давление равно соответственно р0 и р. Если напряжение массовой силы обладает потенциалом, то есть
2. Равновесие жидкости в поле силы тяжести
Уравнение (9) справедливо для любой точки в объеме жидкости. Уравнение изобары имеет в рассматриваемом случае вид
Таким образом, при равновесии жидкости, находящейся в поле силы тяжести, изобара представляет собой горизонтальную плоскость. Для определения константы С в уравнении (9) необходимо задать граничные условия. Пусть при z=z0 p=p0 (см. рис. 1). Тогда p-p0=ρg(z0-z), (11) или
Обозначив z0 -z=h, уравнение (11) можно представить в виде p=p0+ρgh. (13) где pgh - давление, создаваемое столбом жидкости высотой h. Уравнение (8), или (12), обычно называются основными уравнениями гидростатики.
Высота Н называется пьезометрической, а поверхность, проходящая через уровень в пьезометре - пьезометрической плоскостью. Если p0> рат, то пьезометрическая плоскость лежит выше свободной поверхности в сосуде, если p0<рат , то ниже. 5. Равновесие тяжелого газа. Для газа, находящегося в равновесии в поле силы тяжести, из (7) имеем
Для вычисления интеграла в (15) необходимо задать зависимость р =p(ρ). Ограничимся рассмотрением изотермического равновесия идеального газа при температуре Тb. Тогда ρ=p/(RT0) и из (15) получим:
Разлагая это выражение в ряд, имеем:
Если
где ρ0 - плотность газа при давлении p0 и температуре То. Из формулы (16) следует, что если z-z0 мало, то распределение давления в газе будет практически таким же, как в несжимаемой жидкости. Для воздуха газовая постоянная R=287дж/(кг град). Пусть T0=293°К. Тогда при z-z0<85м погрешность, даваемая формулой (16), будет меньше 1%. 3. Относительный покой жидкости Как уже указывалось, при рассмотрении относительного покоя жидкости под напряжением массовой силы в уравнениях (2) следует понимать равнодействующую напряжений силы тяжести и силы инерции переносного движения. Рассмотрим задачу о вращении с постоянной угловой скоростью ωсосуда с жидкостью вокруг вертикальной оси Оz (рис. 6). На элемент жидкости массой ∆m действует сила тяжести и центробежная сила, напряжения которых равны
где ř ~ вектор, направленный по кратчайшему расстоянию от оси вращения к рассматриваемому элементу. Проекции этих напряжений на выбранные оси координат O.xyz равны
Подставив эти значения в уравнения (4) и (5), имеем
Интегрируя эти соотношения, получим
Для определения высоты Н параболоида положим в уравнении (20) r = R , где R - радиус сосуда. Тогда
Из уравнения (20) имеем
Таким образом, если отсчитывать координату z от свободной поверхности, то распределение давления по вертикали во вращающемся сосуде будет таким же, как и в покоящейся жидкости. Это объясняется тем, что проекция силы инерции на ось 0z равна нулю. Полученный результат следует также непосредственно из формулы (3). Действительно, в рассматриваемом случае
откуда после интегрирования сразу получается формула (21). Рассмотрим теперь движение сосуда с жидкостью по наклонной плоскости с постоянным ускорением ā(рис. 7).
Из соотношения (23), представляющего собой уравнение семейства изобар, получим
то есть изобары представляют собой плоскости, наклоненные иод углом β к горизонту. Интегрируя уравнение (22), получим закон распределения давления
Для определения константы интегрирования С положим, что в точке H(xo,0,z0) р=р0. Тогда
Рассмотрим некоторые частные случаи. а) Спуск по вертикальной стене, то есть а =π/2. Из формулы (24) следует, что β=0, z=const. Изобары представляют собой горизонтальные плоскости. Из формулы (25) имеем
При свободном падении j = g и р = р0, то есть давление во всех точках жидкости одинаково. Единственной действующей на жидкость силой будет поверхностное натяжение, под действием которого жидкость стягивается в шар. б) Скольжение по плоскости без трения. В этом случае j=gsinαи из формулы (24) получим, что tgβ=tgα, то есть эквипотенциали параллельны плоскости скольжения. Из формулы (25) имеем
Поиск по сайту: |
 , (1)
, (1) и, соответственно, εik=0.
и, соответственно, εik=0. ):
): . (2)
. (2) , имеем
, имеем , (3)
, (3) определяется проекцией напряжения массовой силы Fs на это направление.
определяется проекцией напряжения массовой силы Fs на это направление. . (4)
. (4)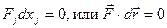 , (5)
, (5) , (6)
, (6) , то соотношение (6) принимает вид:
, то соотношение (6) принимает вид: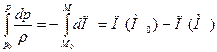 . (7)
. (7)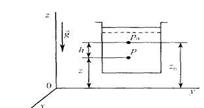 Рис. 6.1.
Рис. 6.1.
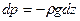 . (8)
В случае однородной несжимаемой жидкости р-const, из уравнения (6.8) имеем
. (8)
В случае однородной несжимаемой жидкости р-const, из уравнения (6.8) имеем
 . (9)
. (9)
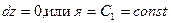 . (10)
. (10) . (12)
. (12)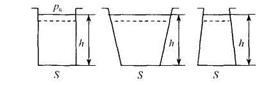 Рис. 2.
Рис. 2.
 Рис.3.
Рис.3.
 Рис. 4.
Рис. 4.
 откуда следует, что р1 - р2 =gh{ρ2-ρ1).
откуда следует, что р1 - р2 =gh{ρ2-ρ1).
 Рис. 5.
Рис. 5.
 Тогда
Тогда  . (14)
Давление в любой точке сосуда равно
. (14)
Давление в любой точке сосуда равно
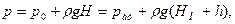
 (15)
(15)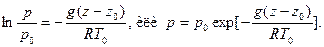


 (16)
(16) ,
,
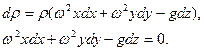
 (17)
(17) (18)
(18) Рис.6.
Рис.6.

 .
. ,
, (21)
(21) ,
, Рис. 7.
Рис. 7.
 где а - угол наклона плоскости к горизонту,
где а - угол наклона плоскости к горизонту,  . Подставив эти значения в уравнения (4) и (5), имеем
. Подставив эти значения в уравнения (4) и (5), имеем

 (24)
(24)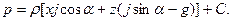
 (25)
(25)