 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные подходы к изучению движения сплошных сред
Изучение движения жидкости может быть произведено с двух точек зрения. С точки зрения Лагранжа: объектом изучения служит сама движущаяся жидкость или отдельные ее частицы, рассматриваемые как материальные частицы, сплошным образом заполняющие движущийся объем жидкости. Здесь изучение состоит: 1) в исследовании изменений, которые претерпевают различные векторные и скалярные величины, характеризующие движение некоторой фиксированной частицы жидкого объема (например, скорость, плотность и т.д.) в зависимости от времени; 2) в исследовании изменений тех же величин при переходе от одной частицы жидкого объема к другой. При этом величины, характеризующие движение, рассматриваются как функции времени и тех чисел, которыми отмечается индивидуальность взятой частицы. За такие числа принимают декартовы координаты жидкой частицы – x0, y0, z0 в некоторый начальный момент времени t0; Тогда при движении жидкого объема координаты частицы будут
причем при t=t0 функции φ1, φ2, φ3 тождественно обращаются в x0, y0, z0 :
Для x0, y0, z0 имеем:
где a, b, c – заданные величины. По Лагранжу переменные t,a,b,c - аргументы, определяющие значение различных векторных и скалярных функций, которыми характеризуется движение жидкости. Это переменные Лагранжа. Таким образом, имеем:
Проекции скорости и ускорения имеют вид:
плотность будет ρ=f(a,b,c,t) и т.д.
С точки зрения Эйлера объектом изучения является не сама жидкость, а неподвижное пространство, заполненное движущейся жидкостью, и изучается: 1) изменение различных элементов движения в фиксированной точке пространства с течением времени; 2) изменение этих элементов при переходе к другим точкам пространства. Иначе говоря, различные векторные и скалярные элементы движения рассматриваются как функции точки и времени c аргументами x, y, z, t – переменные Эйлера. Например, v=F(r, t) или
и т.д. Таким образом, по Эйлеру объектами изучения являются различные векторные и скалярные поля, характеризующие движение жидкости, например, поле скорости, поле ускорений, поле плотностей и т.д. Переход от переменных Лагранжа к переменным Эйлера и обратно может быть осуществлен при помощи уравнений (2), которые должны иметь однозначные решения относительно a,b,c:
Из взаимной разрешимости уравнений (2) и (6) следует, что ни один из функциональных определителей
не обращаются в нуль или бесконечность. Пусть, например, некоторая величина A задана в переменных Эйлера A=F(x,y,z,t) и требуется составить ее производные по переменным Лагранжа; тогда имеем:
Заметим, что (8) дает выражение для полной или индивидуальной производной функции F:
Применяя (9) к функциям vx, vy, vz, имеем выражения для проекций ускорения в переменных Эйлера:
Обратный переход от переменных Эйлера к переменным Лагранжа может быть произведен при помощи уравнений (5), которые в переменных Лагранжа принимают вид:
Интегрируя эти уравнения, найдем
где c1, c2, c3 – произвольные постоянные, появляющиеся вследствие интегрирования. Полагая a=c1, b=c2, c=c3, приходим к уравнениям (2), определяющим движение в переменных Лагранжа.
Поиск по сайту: |
 (1)
(1)
 ,
, (2)
(2)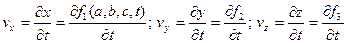 ; (3)
; (3) , (4)
, (4) , (5)
, (5) (6)
(6)
 ; (7)
; (7) . (8)
. (8) . (9)
. (9)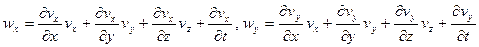
 (10)
(10) . (11)
. (11) , (12)
, (12)