 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Напряженное состояние деформируемой среды
Когда сплошное тело приходит в движение, каждый элемент жидкости с течением времени в общем случае перемещается в новое положение и при этом деформируется. Движение жидкости будет полностью определено, если вектор скорости Ŵ будет задан, т.е. Ŵ=f(x,y,z,t). Поэтому должно существовать соотношение между составляющими скорости деформации и функцией Ŵ= Ŵ(x,y,z,t). Скорость, с которой элемент жидкости деформируется, зависит от относительного движения двух точек. Рассмотрим 2 близкие точки (A,B). При наличии поля скоростей т.А за промежуток времени dt совершает перемещение s= Ŵdt в положение Считаем, что в т.А составляющие скорости Ŵ есть u,v,w. Тогда составляющие скорости в т.В будут
(1)
Система (1) получена с учетом разложения в ряд Тейлора скорости Ŵ+d Ŵ, сохраняя при этом только члены первого порядка. Таким образом, относительное движение т.В относительно т. А будет описываться матрицей из 9 частных производных локального поля скорости
Преобразуем (1) составляющие относительной скорости du, dv, dw к виду:
Введенные символы имеют значения
и
Заметим, что Каждый член в (4), (5) имеет геометрическую и физическую интерпретацию или физический смысл. Уравнения (3) определяют поле относительных скоростей, в котором du,dv,dw являются линейными функциями пространственных координат. Смысл членов в (4), (5). Величины Компоненты завихренности поля скоростей В общем случае движение элемента жидкости может быть разложено на 4 составляющих: 1) на чистое параллельное перемещение, определяемое составляющими скорости u,v,w. 2) на вращение как твердого тела, определяемое составляющими 3) на объемное расширение, определяемое величиной 4) на искажение геометрической формы, определяемое величинами Элементы матрицы (4) образуют систему составляющих симметричного тензора – тензора скоростей деформации. Тензор напряжений
Когда жидкость покоится, в ней существует однородное поле гидростатического давления (отрицательное давление -p). Если же жидкость движется, то уравнение состояния должно определять также давление в каждой точке (принцип локального состояния), и поэтому нормальные напряжения есть
Нормальные и касательные напряжения
4.1. Идеальная жидкость, ее тензор напряжений Жидкость называется идеальной, если в ней отсутствуют касательные напряжения и наблюдаются только нормальные напряжения. В реальных жидкостях касательные напряжения не равны нулю, но часто встречаются случаи, когда касательные напряжения малы по сравнению с нормальными. Именно в этих случаях рассматривают среды, как идеальные. Во всех случаях справедлива формула Коши
По определению идеальной жидкости
Подставляя (2) в (1), имеем
Поскольку
из (3) следует, что
Формулы (2) перепишутся в виде
Из (6) следует, что в идеальной жидкости величина нормального напряжения не зависит от ориентировки площадки. Величина p наз. давлением. Из (6) следует, что составляющие тензора напряжений
Вязкая жидкость Вязкой жидкостью наз. жидкость, в которой при движении кроме нормальных напряжений наблюдаются и касательные напряжения. Причиной вязкости касательных напряжений является хаотическое движение молекул, переход из слоя в слой создает торможение движущихся слоев относительно друг друга. Жидкость наз. вязкой ньютоновской, если выполнены условия: 1) в жидкости, когда она движется как абсолютно твердое тело или находится в покое, наблюдаются только нормальные напряжения; 2) компоненты тензора напряжений есть линейные функции компонент тензора скоростей деформаций; 3) жидкость изотропна, т.е. ее свойства одинаковы по всем направлениям Условия 1) означает, что Таким образом, связь между тензором напряжений и тензором скоростей деформаций в любых осях координат имеет вид
Из (1) составляющие тензора напряжений в вязкой жидкости будут:
Замечание. Если 5.1. Нетеплопроводная среда. Жидкость называется нетеплопроводной, если вектор потока тепла q равен нулю. Схему нетеплопроводной жидкости используют в случае, когда явление теплопроводности оказывает малое влияние на физический процесс, и обычно принимают одновременно с предположением об идеальной жидкости. Уравнение энергии для идеальной нетеплопроводной жидкости имеет вид:
Для широкого класса изотропных сред справедлив закон теплопроводности Фурье: количество тепла dq, прошедшее внутрь за время dt через площадку dS с нормалью n, пропорционально dSdt и производной от температуры по нормали: Жидкость называется несжимаемой, если ее плотность в частице при движении сохраняется. В переменных Эйлера это означает:
При условии (4) уравнение неразрывности будет 5.2. Сжимаемая жидкость. В общем случае плотность является функцией давления и температуры. Уравнение, связывающее плотность давление и температуру – уравнение состояния Ф (ρ, p, T)=0. (5) Для идеальных в термодинамическом смысле газов уравнение состояния – уравнение Клапейрона
где V – уд. объем, R0 – универсальная газовая постоянная. Этому уравнению подчиняются многие газы, если давление p не очень большое и температура T не слишком низкая. При более высоких давлениях часто используют уравнение Ван дер Ваальса
Поиск по сайту: |
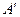 , т. В с радиусом вектором dr по отношению к т.А перемещается в положение
, т. В с радиусом вектором dr по отношению к т.А перемещается в положение 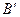 , расположенное относительно т.В согласно радиусу-вектору s+ds= (Ŵ+d Ŵ)dt.
, расположенное относительно т.В согласно радиусу-вектору s+ds= (Ŵ+d Ŵ)dt.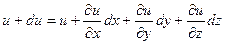
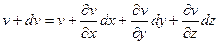
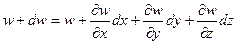 .
.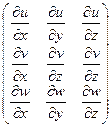 (2)
(2)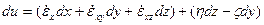
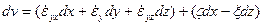 (3)
(3)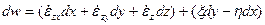
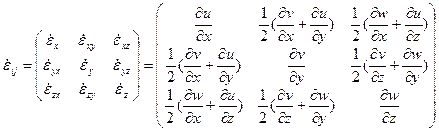 (4)
(4)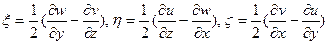 . (5)
. (5)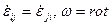 Ŵ.
Ŵ.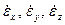 представляют удлинение элемента жидкости в направлении x,y,z соответственно. Общее удлинение есть
представляют удлинение элемента жидкости в направлении x,y,z соответственно. Общее удлинение есть 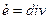 Ŵ – объемное расширение или сжатие жидкости. Каждый из диагональных членов
Ŵ – объемное расширение или сжатие жидкости. Каждый из диагональных членов 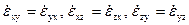 определяет скорость искажения прямого угла, лежащего в плоскости, нормальной к оси, индекс которой отсутствует в двойном индексе недиагонального члена матрицы (4). Это искажение сохраняет объем и изменяет только форму элемента жидкости.
определяет скорость искажения прямого угла, лежащего в плоскости, нормальной к оси, индекс которой отсутствует в двойном индексе недиагонального члена матрицы (4). Это искажение сохраняет объем и изменяет только форму элемента жидкости.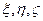 вектора
вектора 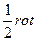 Ŵ представляют угловые скорости мгновенного вращения элемента жидкости как твердого тела.
Ŵ представляют угловые скорости мгновенного вращения элемента жидкости как твердого тела.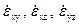 .
.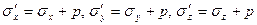 . (1)
. (1)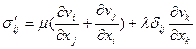 образуют симметричный тензор напряжений, существование которого обязано движению. Полная интерпретация требует воспользоваться тензорным исчислением (см. сноски).
образуют симметричный тензор напряжений, существование которого обязано движению. Полная интерпретация требует воспользоваться тензорным исчислением (см. сноски).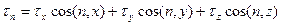 . (1)
. (1)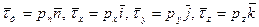 . (2)
. (2)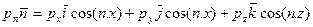 . (3)
. (3)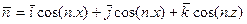 , (4)
, (4)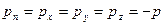 . (5)
. (5)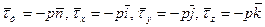 . (6)
. (6)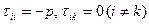 . Тензор напряжений идеальной жидкости будет иметь вид
. Тензор напряжений идеальной жидкости будет иметь вид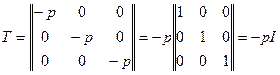 . (7)
. (7)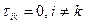 , если все
, если все 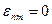 . Условие 2) означает, что
. Условие 2) означает, что 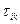 могут быть представлены через
могут быть представлены через 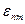 , учитывая симметрию тензора напряжений. Условие 3) означает, что коэффициенты в связи
, учитывая симметрию тензора напряжений. Условие 3) означает, что коэффициенты в связи 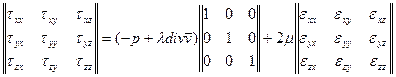 . (1)
. (1) ;
;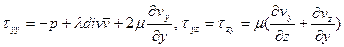 ; (2)
; (2)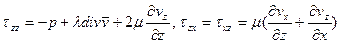 .
. , то тензор напряжений вязкой жидкости обращается в тензор напряжений идеальной жидкости. Здесь μ – коэффициент сдвиговой вязкости, λ – коэффициент объемной вязкости.
, то тензор напряжений вязкой жидкости обращается в тензор напряжений идеальной жидкости. Здесь μ – коэффициент сдвиговой вязкости, λ – коэффициент объемной вязкости.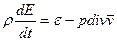 . (3)
. (3)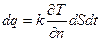 .
. или
или 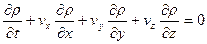 . (4)
. (4)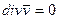 . Схему несжимаемой жидкости используют при рассмотрении движений капельных жидкостей, а также при рассмотрении движений газов с небольшими скоростями.
. Схему несжимаемой жидкости используют при рассмотрении движений капельных жидкостей, а также при рассмотрении движений газов с небольшими скоростями.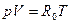 , (6)
, (6)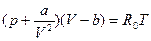 . (7)
. (7)