 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Глава 13. Основные положения задачи об истечении капельных сред из замкнутых систем
Понятия и определения При рассмотрении многих технических вопросов, как истечение жидкости из резервуаров различного назначения, утечки через свищи в трубопроводах, распыление жидкости через форсунки приходится сталкиваться с задачами истечения через отверстия и насадки. 1.1. Истечение из малого отверстия. Для примера рассматривается резервуар, в днище которого имеется круглое отверстие диаметра d. Особенность истечения связана с тем, что струя, вытекая, сжимается и на некотором расстоянии l приобретает площадь сечения ωc, меньшую, чем площадь отверстия ω. Величина
наз. коэффициентом сжатия струи. Если стенки резервуара (Р) не влияют на формирование струи, то сжатие наз. совершенным. Наоборот – несовершенным. Из опыта следует, чтобы сжатие было совершенным необходимо, чтобы расстояние от стенки с>3d. Если по части периметра отверстия имеются направляющие козырьки, то сжатие наз. неполным. Наоборот – полным. Для определения скорости истечения из отверстия воспользуемся уравнением Бернулли для участка между сечениями (0 – свободная поверхность, с – место, где заканчивается сужение). Тогда
Также из уравнения неразрывности следует, что
где ω0 – площадь Р в сечении 0. Из опыта следует, что l≈d и l<<H. Все потери напора сосредоточены в отверстии, которое является местным сопротивлением. Согласно формуле Дарси-Вейсбаха имеем:
С учетом (3), (4) из (2) имеем
Из (5) следует, что скорость истечения wc будет
Здесь
В приведенных обозначениях по (7), (8) cвязь (6) имеет вид
Замечание. Величины α0 >1, αс >1; ς>0, благодаря вязкости; ε<1 из-за наличия инерции. Поэтому φ учитывает вязкостные и инерционные эффекты. Определение. Если для отверстия выполняется
(10) наз. теоретической скоростью истечения. Расход через отверстие равен
Величина μ=εφ наз. коэффициентом расхода. Таким образом, параметры ε, φ, μ не являются независимыми, а связаны соотношением. Они определяются экспериментально и являются функциями числа Рейнольдса. С помощью уравнения Бернулли можно показать, что для малого отверстия (9) и (11) будут справедливы и в том случае, если отверстие находится в боковой стенке Р. При этом под H понимают расстояние от оси отверстия до свободной поверхности. Истечение при ламинарном режиме. Для ламинарного истечения, путем интегрирования ДУ движения реальной жидкости, может быть получена формула для скорости истечения Семпсона:
Истечение из насадок
Основные понятия и определения. Насадками (Н) наз. трубки различных форм и размеров, приставляемые к отверстию, через которое происходит истечение жидкости. Длина Н составляет 3-5 диаметров отверстия. Характер истечения существенно зависит от формы Н. Из формул (9), (11) видно, что они справедливы и для истечения через Н. Однако, коэффициенты φ, μ будут зависеть от вида Н. Различают следующие типы Н: 1) внешний цилиндрический; 2) внутренний цилиндрический; 3) конический сходящийся; 4) конический расходящийся; 5) коноидальный. Приводятся значения φ, μ этих Н. Для некоторых типов Н φ= μ, тогда ε=1. Это объясняется тем, что сжатие струи происходит внутри этих Н. Замечание. При прочих равных условиях расход через внешний цилиндрический Н на 30% больше, чем через круглое отверстие того же диаметра. Цилиндрический Н. При входе в Н струя сжимается, а затем расширяется. При этом в области сжатия образуется застойная зона, заполненная вихрями. На основе уравнения Бернулли, записанного для области сечений внутри цилиндрического Н, закона изменения количества движения (для определения потерь напора на внезапное расширение струи), выражения массового расхода, имеем сооотношене Борда для участка 1-2 Н
Из уравнения неразрывности для струи имеем
где εвх – коэффициент сжатия струи при входе в Н. С учетом (1), (2) уравнение Бернулли имеет вид в нашем случае
Т.к. εвх<1 то из (3) следует, что p1<p2, то есть в сечении 1 имеется разрежение, что приводит к увеличению расхода по сравнению с круглым отверстием. При истечении в атмосферу p2=pатм и в сечении 1 образуется вакуум. Величина этого вакуума равна Существует предельное значение Для Н имеем
Из (4) можно определить значение l/d, при котором расход через Н равен расходу через отверстие. Истечение жидкости при переменном уровне. Рассматривается истечение жидкости через малое отверстие или Н при переменном уровне в резервуаре. Условия течения нестационарные, площадь поперечного сечения резервуара Ω зависит от высоты z. Приравнивая объемы вытекающей через отверстия жидкости и опустившийся в резервуаре за счет этого процесса за время dt, имеем
Учитывая (11, Темы 7), имеем
Или т.к. Из (7) следует, что время опускания уровня в резервуаре от отметки z1 до z2 равно
В соответствием с (8) имеем: 1. Истечение из вертикального цилиндра (Ω=const).
2. Истечение из горизонтального кругового цилиндра.
3. Истечение из сферического резервуара.
Поиск по сайту: |
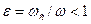 (1)
(1)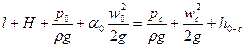 . (2)
. (2) , (3)
, (3)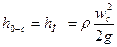 . (4)
. (4)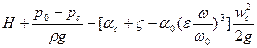 . (5)
. (5) . (6)
. (6) - напор истечения. (7)
- напор истечения. (7) - коэффициент скорости. (8)
- коэффициент скорости. (8) . (9)
. (9) , то отверстие наз. малым. Для него (9) сохраняет свой вид, но коэффициент скорости равен
, то отверстие наз. малым. Для него (9) сохраняет свой вид, но коэффициент скорости равен  . (В указанных допущениях φ<1). Для идеальной жидкости (αс =1, ς=0). Тогда φ=1 и (9) имеет вид
. (В указанных допущениях φ<1). Для идеальной жидкости (αс =1, ς=0). Тогда φ=1 и (9) имеет вид . (10)
. (10) или
или  . (11)
. (11) . (12)
. (12) . (1)
. (1) , (2)
, (2) . (3)
. (3)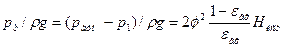 и тем больше, чем больше напор истечения.
и тем больше, чем больше напор истечения. , выше которого работа Н нарушается, происходит отрыв струи от его стенок и расход резко уменьшается. При этом истечение происходит также через отверстие. Явление отрыва струи от стенок наз. срывом истечения. С увеличением длины Н сказывается увеличение потерь на трение по его длине.
, выше которого работа Н нарушается, происходит отрыв струи от его стенок и расход резко уменьшается. При этом истечение происходит также через отверстие. Явление отрыва струи от стенок наз. срывом истечения. С увеличением длины Н сказывается увеличение потерь на трение по его длине. . (4)
. (4) . (5)
. (5) . (6)
. (6) , то
, то  . (7)
. (7) . (8)
. (8) (9)
(9) . Тогда из (8) будет
. Тогда из (8) будет . (10)
. (10) , где b – определяется из (10). Тогда
, где b – определяется из (10). Тогда 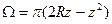 и
и . (11)
. (11)