 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоремы динамики жидкости
Теорема Бернулли для сжимаемой жидкости. При выводе теоремы используется такой же метод, как и в случае несжимаемой жидкости. Однако здесь учитывается внутренняя энергия газа. В результате ТБ имеет форму
Применение ТБ к адиабатному расширению. При адиабатном расширении газа имеет место +
Теорема Торричелли. Формулировка теоремы в задачах об истечении из резервуара сводится к связи для скорости истечения Теорема Эйлера о количестве движения. Утверждает, что если пренебречь массовыми силами, то результирующая сила, обусловленная давлением окружающей жидкости стенки и концы трубки, эквивалентна силам Парадокс Даламбера. Рассматривается прямая трубка, в которой течет невязкая жидкость с постоянной скоростью. Если в середину трубки поместить тело, поток вблизи него изменится, но вдалеке от входа и выхода поток остается невозмущенным. Чтобы тело было в покое к нему необходимо приложить силы. Парадокс Даламбера состоит в том, что в указанных условиях компонента силы в направлении потока равна нулю. Следовательно, сопротивление тела, движущегося с постоянной скоростью в неограниченной невязкой покоящейся жидкости, будет равно нулю. Определения. Вихрь. Вектор
Теорема Гаусса. Формулировка теоремы сводится к выражению
Здесь X – скалярная или векторная функция, зависящая от координат точки в пространстве, V – объем, S – поверхность объема. Следствия теоремы сводятся к равенствам:
Теорема Грина. Содержание теоремы сводится к следующему соотношению:
Соотношение (4) - первое тождество Грина. Второе тождество Грина имеет вид
Данные теоремы и их результаты важны при анализе многосвязных поверхностей. Формулы позволяют определять значение функции в произвольной точке внутри области через значения этой функции на границе области. Кинетическая энергия жидкости. Определяется интегралом
Здесь интегралы берутся по граничной поверхности жидкости, при этом dn обозначает элемент нормали, проведенной внутрь жидкости. Физическая интерпретация. Т.к. действительное движение может возникнуть из состояния покоя под действием импульсивного давления ρφ и поскольку Работа, совершенная импульсом за единицу времени, равна произведению импульса на полусумму компонент в его направлении начальной и конечной скоростей точки, на которую он действует. Следовательно, поверхностный интеграл представляет собой работу, совершаемую импульсивным давлением, если движение начинается из состояния покоя. Теорема Кельвина о минимуме энергии. Безвихревое движение жидкости, занимающей односвязную область, имеет меньшую кинетическую энергию, чем любое другое движение с теми же самыми нормальными компонентами скорости на границе. Доказательство приводится.
Поиск по сайту: |
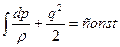 вдоль линии тока, откуда получаем dp=-ρqdq.
вдоль линии тока, откуда получаем dp=-ρqdq.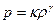 ,
,  . Т.к. величина p0/ρ0 относится к начальному состоянию, то она является константой. Из ТБ имеем
. Т.к. величина p0/ρ0 относится к начальному состоянию, то она является константой. Из ТБ имеем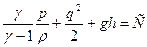 . (1)
. (1)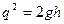 . Выражение получено с использованием ТБ.
. Выражение получено с использованием ТБ.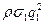 и
и  , приложенным к концевым сечениям и направленным по внешним нормалям к ним.
, приложенным к концевым сечениям и направленным по внешним нормалям к ним.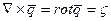 наз. вектором вихря. Вихревая линия – линия в жидкости, касательная в каждой точке которой направлена вдоль вектора вихря в этой точке. Если вихрь отличен от нуля, то движение вихревое и наоборот. Циркуляция представляется в одной из следующих форм:
наз. вектором вихря. Вихревая линия – линия в жидкости, касательная в каждой точке которой направлена вдоль вектора вихря в этой точке. Если вихрь отличен от нуля, то движение вихревое и наоборот. Циркуляция представляется в одной из следующих форм: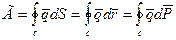 (2)
(2)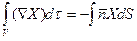 . (3)
. (3)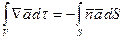 ,
, 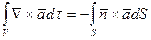 ,
, 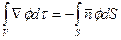 и т.д.
и т.д.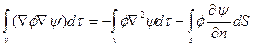 . (4)
. (4) . (5)
. (5)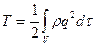 , взятым по объему V, занимаемому жидкостью. Если движение безвихревое, то
, взятым по объему V, занимаемому жидкостью. Если движение безвихревое, то 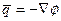 . Следовательно, если потенциал скоростей φ однозначен, то из условия
. Следовательно, если потенциал скоростей φ однозначен, то из условия 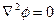 и теоремы Грина имеем:
и теоремы Грина имеем: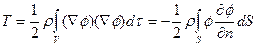 . (6)
. (6) - скорость жидкости, нормальная к границе, то величина
- скорость жидкости, нормальная к границе, то величина 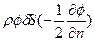 - работа, совершенная за единицу времени импульсивным давлением, действующим на элемент ΔS в соответствии со следующей теоремой динамики.
- работа, совершенная за единицу времени импульсивным давлением, действующим на элемент ΔS в соответствии со следующей теоремой динамики.