 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Движение материальной точки в неинерциальной системе отсчета
1.4.1. Дифференциальное уравнение динамики относительного движения точки. Запишем сначала дифференциальное уравнение динамики точки в инерциальной системе отсчета
где Формула, связывающая ускорения точки в неподвижной и подвижной системах отсчета, была получена в курсе кинематики:
где Поскольку неподвижная система отсчета инерциальная, подставим (1.22) в (1.21) и запишем дифференциальное уравнение в виде
Слагаемые Сопоставление уравнений (1.21) и (1.23) показывает, что в инерциальной системе отсчета ускорение материальной точки является результатом действия приложенных к ней сил, т.е. взаимодействия с другими материальными телами; в неинерциальной системе ускорение материальной точки является как результатом действия на нее сил, так и результатом движения самой системы. Если действие сил является динамической причиной движения точки с некоторым ускорением, то движение системы отсчета по отношению к инерциальной системе можно назвать кинематической причиной появления ускорения. Силы инерции Если движение происходит длительное время, то влияние сил инерции - размывание реками правых берегов (закон Бэра); - отклонение вправо морских течений и дрейфующих льдов; - отклонение вправо ветров постоянного направления; - отклонение снарядов и ракет вправо от плоскости стрельбы; - больший износ правого рельса по сравнению с левым на двухколейных железных дорогах; - отклонение падающих тел к востоку.
1.4.2. Частные случаи. Движение подвижной системы отсчета (переносное движение материальной точки) определяет вид основного уравнения динамики относительного движения материальной точки. Так, если переносное движение – поступательное (в общем случае – криволинейное), то
Тогда уравнение (1.23) принимает вид
В том случае, когда переносное движение поступательное (
Если переносное движение будет поступательным, прямолинейным и равномерным (
В этом случае подвижная система отсчета так же, как и неподвижная, будет инерциальной. Очевидно, что сделанный вывод позволяет в предыдущих рассуждениях заменить термин неподвижная система отсчета на более общий термин инерциальная. Отсутствие принципиальной возможности каким-либо механическим опытом, основанным на наблюдении за движением материальных тел, отличить одну инерциальную систему отсчета от другой лежит в основе принципа относительности классической механики. Этот принцип утверждает: все механические явления в различных инерциальных системах отсчета протекают одинаково; либо - никаким механическим опытом нельзя обнаружить инерциальное движение системы отсчета, участвуя вместе с ней в этом движении. Если переносно движение – вращение вокруг неподвижной оси, то
Если вращение происходит с постоянной угловой скоростью
1.4.3. Условие относительного покоя. В этом случае относительная скорость и относительное ускорение точки равны нулю, следовательно, равна нулю и сила инерции Кориолиса. Тогда уравнение относительного покоя будет иметь вид
ПРИМЕР 1.5 (задача 33.10 из [2]). Горизонтальная трубка СD равномерно вращается вокруг вертикальной оси АВ с угловой скоростью РЕШЕНИЕ. Свяжем с неподвижными опорами и землей неподвижную инерциальную систему
Движение шарика по трубке примем за относительное движение, а вращение вместе с трубкой – за переносное. Воспользовавшись формулами кинематики, будем иметь
Вычислим соответствующие силы инерции
Воспользуемся заменой
Окончательно имеем: Заметим, что проецирование действующих сил на ось ПРИМЕР 1.6. Призма движется по плоскости с постоянным ускорением
РЕШЕНИЕ. Свяжем с плоскостью неподвижную координатную систему На рис.1.10 изобразим призму, груз и силы, на него действующие ( вес Спроецировав слагаемые уравнения относительного покоя (1.28) на ось
Отсюда величина искомого угла будет
Поиск по сайту: |
 (1.21)
(1.21) - равнодействующая всех задаваемых сил,
- равнодействующая всех задаваемых сил,  - равнодействующая сил реакций.
- равнодействующая сил реакций. , (1.22)
, (1.22) - ускорение Кориолиса;
- ускорение Кориолиса;  - угловая скорость вращения подвижной системы относительно неподвижной;
- угловая скорость вращения подвижной системы относительно неподвижной; 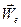 - ускорение точки подвижной системы отсчета, с которой в данный момент совпадает рассматриваемая точка (переносное ускорение);
- ускорение точки подвижной системы отсчета, с которой в данный момент совпадает рассматриваемая точка (переносное ускорение);  - скорость и ускорение точки в подвижной системе отсчета (относительные скорость и ускорение).
- скорость и ускорение точки в подвижной системе отсчета (относительные скорость и ускорение). . (1.23)
. (1.23) и
и  называются, соответственно, переносной силой инерции и силой инерции Кориолиса. Уравнение (1.23) представляет собой основное уравнение динамики материальной точки, записанное в системе отсчета, движение которой по отношению к неподвижной (инерциальной) системе отсчета известно. Ниже такие системы отсчета будем называть неинерциальными.
называются, соответственно, переносной силой инерции и силой инерции Кориолиса. Уравнение (1.23) представляет собой основное уравнение динамики материальной точки, записанное в системе отсчета, движение которой по отношению к неподвижной (инерциальной) системе отсчета известно. Ниже такие системы отсчета будем называть неинерциальными. и
и  можно рассматривать как поправки к закону Ньютона на неинерциальность подвижной системы отсчета. Если в рамках конкретной задачи их величинами можно пренебречь по сравнению с остальными действующими на материальную точку силами, то рассматриваемую подвижную систему отсчета полагают инерциальной. Так, например, поступают при изучении движения тел с малыми скоростями относительно Земли. Но при скорости 1000м/с и выше (с которыми движутся снаряды, самолеты и ракеты) введение в основное уравнение динамики слагаемых
можно рассматривать как поправки к закону Ньютона на неинерциальность подвижной системы отсчета. Если в рамках конкретной задачи их величинами можно пренебречь по сравнению с остальными действующими на материальную точку силами, то рассматриваемую подвижную систему отсчета полагают инерциальной. Так, например, поступают при изучении движения тел с малыми скоростями относительно Земли. Но при скорости 1000м/с и выше (с которыми движутся снаряды, самолеты и ракеты) введение в основное уравнение динамики слагаемых  (т.к.
(т.к.  ), а
), а , где
, где 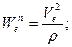
 .
. . (1.24)
. (1.24) ), в полученном уравнении будет отсутствовать последнее слагаемое, т.е.
), в полученном уравнении будет отсутствовать последнее слагаемое, т.е. . (1.25)
. (1.25)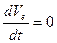 ), будут равны нулю все силы инерции; при этом вид уравнения аналогичен (1.21), т.е.
), будут равны нулю все силы инерции; при этом вид уравнения аналогичен (1.21), т.е. (1.26)
(1.26)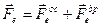 ; где
; где  ;
;  ;
;  , а уравнение (1.23) принимает вид
, а уравнение (1.23) принимает вид
 (1.27)
(1.27) . (1.28)
. (1.28) . Внутри трубки находится шар М. Определить скорость
. Внутри трубки находится шар М. Определить скорость 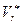 шара относительно трубки в момент его вылета, если в начальный момент
шара относительно трубки в момент его вылета, если в начальный момент 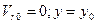 , длина трубки
, длина трубки  . Трением пренебречь.
. Трением пренебречь. . С трубкой свяжем подвижную координатную систему
. С трубкой свяжем подвижную координатную систему  и для некоторого промежуточного момента времени изобразим (см. рис.1.9) трубку и шарик с действующими на него силами (включая силы инерции).
и для некоторого промежуточного момента времени изобразим (см. рис.1.9) трубку и шарик с действующими на него силами (включая силы инерции).
 ;
; 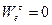 ;
;  .
. и
и 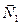 и горизонтальную
и горизонтальную  составляющие силы нормального давления со стороны трубки. Спроецировав соответствующие члены уравнения (1.23) на ось
составляющие силы нормального давления со стороны трубки. Спроецировав соответствующие члены уравнения (1.23) на ось 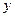 , получим дифференциальное уравнение:
, получим дифференциальное уравнение: .
.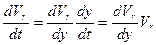 и разделим переменные. Возьмем определенные интегралы от левой и правой частей уравнения:
и разделим переменные. Возьмем определенные интегралы от левой и правой частей уравнения: .
.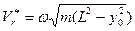 .
.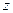 позволяет определить вертикальную составляющую реакции
позволяет определить вертикальную составляющую реакции  , а проецирование на ось
, а проецирование на ось 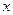 - горизонтальную как
- горизонтальную как  .
.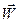 . На гладкой наклонной плоскости призмы находится груз М. Найти угол
. На гладкой наклонной плоскости призмы находится груз М. Найти угол 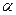 , при котором груз будет неподвижен относительно призмы.
, при котором груз будет неподвижен относительно призмы.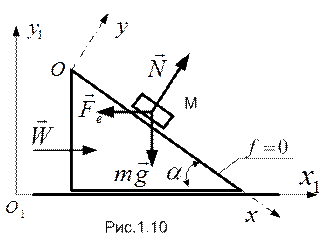
 , а подвижную координатную систему
, а подвижную координатную систему  - с призмой. Тогда движение груза по призме будет его относительным движением, а поступательное вместе с призмой (с ускорением
- с призмой. Тогда движение груза по призме будет его относительным движением, а поступательное вместе с призмой (с ускорением 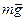 , реакция гладкой поверхности
, реакция гладкой поверхности  ).
). .
. .
.