 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Численное моделирование процесса движения материальной точки методом Эйлера
При достаточно простой структуре силы В качестве примера рассмотрим применение метода численного интегрирования Эйлера для решения указанной задачи. Напомним суть метода численного интегрирования Эйлера: если при некотором значении аргумента
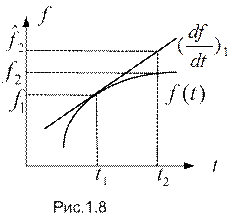
Графическая интерпретация сказанного приведена на рисунке 1.8, где элемент кривой на отрезке изменения аргумента от
Более подробно о методе численного интегрирования Эйлера и особенностях его применения для моделирования процесса движения можно прочитать, например, в [5] или [8]. Перепишем уравнение основного закона динамики материальной точки (1.5) в виде
Из (1.19) следует, что основной закон определяет приращения Заменив в (1.19) бесконечно малые приращения
Зависимости (1.20) носят рекуррентный характер и позволяют последовательно находить (разумеется, приближенно) положение и скорость точки, идя от ее начального положения. Ясно, что точность решения повышается с уменьшением шага Заметим, что решая таким образом уравнения движения свободной материальной точки мы непосредственно моделируем в числах соответствующий процесс, не нарушая причинно-следственные связи, но внося в них некоторые погрешности, т.е. возмущения, неизбежные при практической реализации процесса. При этом если устойчивость самого процесса движения достаточна, то будет достаточной и устойчивость счета, т.е. результаты его будут сравнительно мало зависеть от погрешностей округления значащих цифр и от замены бесконечно малых шагов хотя и малыми, но конечными шагами. Наоборот, неустойчивость счета, т.е. резкое изменение результатов в зависимости от шага расчета и округления значащих цифр, говорит о неустойчивости самого процесса движения. В последнем случае расчетная оценка движения каким-либо способом вообще оказывается бессмысленной.
Поиск по сайту: |
 уравнения (1.5) могут быть проинтегрированы в квадратурах и получено аналитическое решение задачи (см. примеры из настоящего параграфа). В более сложных случаях следует воспользоваться средствами вычислительной техники.
уравнения (1.5) могут быть проинтегрированы в квадратурах и получено аналитическое решение задачи (см. примеры из настоящего параграфа). В более сложных случаях следует воспользоваться средствами вычислительной техники. известны значение функции
известны значение функции  и значение ее первой производной
и значение ее первой производной  , то в момент времени
, то в момент времени  значение
значение 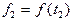 может быть приближенно вычислено, как:
может быть приближенно вычислено, как: . (1.18)
. (1.18) заменяется элементом прямой с углом наклона, равным углу наклона касательной в точке
заменяется элементом прямой с углом наклона, равным углу наклона касательной в точке  ), тем меньше отличается приближенное значение
), тем меньше отличается приближенное значение 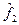 от точного решения
от точного решения 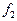 .
.
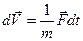 ;
;  . (1.19)
. (1.19) и
и  величин
величин  и
и 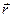 за промежуток времени
за промежуток времени  , т.е. характеризует изменение во времени параметров состояния движения (положение и скорость) материальной точки под действием приложенной к ней силы
, т.е. характеризует изменение во времени параметров состояния движения (положение и скорость) материальной точки под действием приложенной к ней силы  . Естественно, что начальные условия
. Естественно, что начальные условия 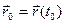 и
и  должны быть заданы.
должны быть заданы.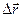 ,
, 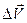 и
и  , получим соотношения
, получим соотношения ;
; ; (1.20)
; (1.20) .
.