 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коэффициент корреляции
Из определения корреляционного момента следует, что его размерность равна произведению размерностей величин Х и Y; например, если Х и Y измерены в сантиметрах, то μxy имеет размерность см2. Это обстоятельство затрудняет сравнение корреляционных моментов различных систем случайных величин. Для устранения этого недостатка вводят безразмерную числовую характеристику — коэффициент корреляции, величина которого не зависит от выбора системы измерения случайных величин. Определение 3. Коэффициентом корреляции случайных величин Х и Y называется отношение их корреляционного момента к произведению средних квадратических отклонений этих величин:
Из определения и свойств математического ожидания и дисперсии следует важный вывод, что абсолютная величина коэффициента корреляции не превосходит единицы:
Определение 4. Две случайные величины Х и Y называются коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля; если же их корреляционный момент равен нулю, то Х и Y называются некоррелированными. Таким образом, две коррелированные случайные величины (т.е. при rxy ≠ 0) являются также и зависимыми. Обратное утверждение неверно, т.е. две зависимые величины могут быть как коррелированными, так и некоррелированными. Пример 2. Найти корреляционный момент и коэффициент корреляции двух случайных величин Х и Y, распределения которых заданы в предыдущем примере 1. Решение. Воспользуемся формулами (18.24), (18.26), а также формулой вычисления центрального момента второго порядка (18.19); последовательно вычисляем: М(Х) = 2,03, М(Y) = 1,63, D(X) = 0,629, D(Y) = 0,233,
В данном случае коэффициент корреляции близок к нулю; это означает, что случайные величины Х и Y слабокоррелированы. Линейная регрессия
Пусть (X, Y) — двумерная случайная величина, где Х и Y — зависимые случайные величины. Оказывается возможным приближенное представление величины Y в виде линейной функции величины X:
где а и b — параметры, подлежащие определению. Обычно эти величины определяются с помощью метода наименьших квадратов (см. п. 8.5). Определение 5. Функция (18.27) называется наилучшим приближением в смысле метода наименьших квадратов, если математическое ожидание M[Y — g(Х)]2 принимает наименьшее возможное значение. Функцию g(х) называют среднеквадратической регрессией Y на X. ТЕОРЕМА 4. Линейная средняя квадратическая регрессия Y на Х имеет вид
где rxy определяется формулой (18.25), ту = M(Y) и mx = М(Х) — математические ожидания соответственно случайных величин Y и X. Коэффициент b = rxуσу / σx называют коэффициентом регрессии Y на Х, а прямую
реализующую линейную зависимость (18.28) случайной величины Y от случайной величины X, называют прямой среднеквадратической регрессии Х на Y. Поскольку зависимость (18.28) является приближенной, то существует погрешность этого приближения, называемая остаточной дисперсией:
Аналогичную форму записи имеет прямая среднеквадратическая регрессия Х на Y:
Пример 3. Найти линейную среднюю квадратическую регрессию и остаточную дисперсию случайной величины Y на случайную величину Х по данным примеров 1 и 2. Решение. Для двумерной случайной величины (X, Y), приведенной в примере 1, все необходимые числовые характеристики указаны в решении примера 2: mx = 2,03, ту = 1,63, rху = -0,023, σx =
Остаточная дисперсия рассчитывается по формуле (18.29):
Для оценки среднеквадратичной погрешности линейной регрессии обычно используют величину ε, в нашем случае она составляет
Поиск по сайту: |


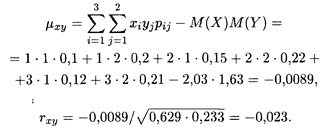


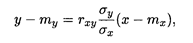

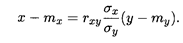
 = 0,793, σy =
= 0,793, σy =  = 0,483. Из уравнения (18.28) получаем искомое соотношение:
= 0,483. Из уравнения (18.28) получаем искомое соотношение:

