 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Асимметрия и эксцесс эмпирического распределения
Нормальное распределение является одним из самых распространенных в применениях математической статистики. Для оценки отклонения эмпирического распределения от нормального используют характеристики, аналогичные для теоретического распределения (см. предыдущий раздел 18.6). Асимметрия эмпирического распределения определяется следующим равенством:
Эксцесс эмпирического распределения определяется следующим равенством:
В формулы (18.62) и (18.63) входят центральные эмпирические моменты, определяемые формулами (18.61), а также выборочное среднее квадратическое отклонение (18.55). Пример 6. Найти асимметрию и эксцесс эмпирического распределения:
Решение. Найдем сначала
Далее, используя формулы (18.61), определяем центральные эмпирические моменты третьего и четвертого порядков:
Затем по формулам (18.62) и (18.63) находим искомые величины:
В заключение отметим, что все оценки, приведенные выше, определяются одним числом, т.е. являются точечными. При малых объемах выборки точечная оценка может приводить к большим ошибкам и значительно отличаться от оцениваемого параметра. УПРАЖНЕНИЯ 18.1. Из коробки с шестью деталями, среди которых четыре стандартные, наудачу взяты три детали. Составить закон распределения дискретной случайной величины Х — количества стандартных деталей среди отобранных. 18.2. Книга издана тиражом 100 тысяч экземпляров. Вероятность брака в книге равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг. 18.3. Случайная составляющая дохода равна 2Х, а случайная составляющая затрат равна 50Y. Найти дисперсию прибыли при условиях: величина Х распределена по биномиальному закону с параметрами п = 100, р = 0,5; величина Y распределена по закону Пуассона с параметром λ = 2; случайные величины Х и Y являются независимыми. 18.4. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной законом распределения
18.5. Найти дисперсию дискретной случайной величины Х — числа отказов элемента некоторого устройства — в 10 независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9. 18.6. Дискретная случайная величина Х задана законом распределения
Найти центральные моменты первого, второго, третьего и четвертого порядков. 18.7. Дано распределение двумерной дискретной случайной величины (X, Y):
Найти ковариацию Cov (X, Y) и коэффициент корреляции Х и Y. 18.8. Непрерывная случайная величина Х задана на всей оси Ох функцией распределения F(x) = 1/2 + (arctg x) / π. Найти вероятность того, что величина Х примет значение, заключенное в интервале (0, 1). 18.9. Случайная величина Х задана функцией распределения
Найти вероятность того, что Х примет значения:а) менее 0,2; б) менее трех;в) не менее трех;г) не менее пяти. 18.10. Дискретная случайная величина задана законом распределения
Найти функцию распределения и построить ее график. 18.11. Дана плотность распределения непрерывной случайной величины X:
Найти функцию распределения F(x). 18.12. Случайная величина Х задана на положительной полуоси Ох функцией распределения F(x) = 1 - e-ax (а > 0). Найти математическое ожидание величины X. 18.13. Случайная величина Х задана на интервале (0,5) плотностью распределения f(x) = 2.x / 25; вне этого интервала f(x) = 0. Найти дисперсию X. 18.14. Случайная величина Х задана плотностью распределения f(x) = е-|x| / 2. Найти математическое ожидание и дисперсию. 18.15. Случайная величина задана функцией распределения
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. 18.16. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2, 8). 18.17. Ребро куба х измерено приближенно в интервале (а, b). Найти математическое ожидание и дисперсию объема куба, если его ребро рассматривать как случайную величину Х с равномерным распределением на указанном интервале. 18.18. Размер мужских сорочек является случайной величиной с нормальным законом распределения, математическим ожиданием 39 и дисперсией 9. Какой процент от общего объема заказа следует предусмотреть магазину для сорочек 40-го размера воротничка при условии, что этот размер находится в интервале (39,5; 40,5)? 18.19. Найти формулу плотности вероятности нормально распределенной случайной величины X, если математическое ожидание равно 3, а дисперсия равна 16. 18.20. Случайная величина Х распределена нормально с математическим ожиданием а = 25. Вероятность попадания Х в интервал (10, 15) равна 0,2. Найти вероятность попадания Х в интервал (35, 40).
Поиск по сайту: |



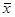 в и σв с использованием формул (18.52)-(18.55):
в и σв с использованием формул (18.52)-(18.55):









