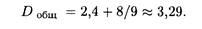|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статистические оценки параметров распределения
Значения количественного признака х1, х2, ..., хk в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок. Несмещенной называется статистическая оценка
Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п. Состоятельной называется статистическая оценка типа (18.50), которая при п > Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
и выборочная средняя
Если значения признака х1, x2, …, хk в выборке имеют соответственно частоты n1, n2, ..., nk, то последнюю формулу можно переписать в виде
Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины. Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это генеральная дисперсия:
и выборочная дисперсия:
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид
Генеральное среднее квадратическое отклонение определяется как
Аналогично вводится и выборочное среднее квадратическое отклонение
Пример 4. Выборка задана таблицей распределения
Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение. Решение. По формуле (18.52) сначала находим
Затем по формулам (18.54) и (18.55) находим две другие искомые величины:
Виды дисперсий
Часто значения количественного признака Х совокупности разбиваются на определенное число групп. Каждую группу можно рассматривать как самостоятельную выборку, и для каждой группы можно определить групповую среднюю и дисперсию. Пусть r — число групп. Групповой дисперсией на зывается дисперсия значений признака в группе относительно групповой средней:
где ni — частота значения xi в группе, j — номер группы Зная дисперсию каждой группы, можно определить их среднюю арифметическую. Внутригрупповой дисперсией называется средняя арифметическая дисперсий, где каждое слагаемое входит с весом объема группы:
В свою очередь, зная для всех групп средние
где п = Для общей дисперсии всей совокупности справедлива следующая теорема, которая приводится здесь без доказательства. ТЕОРЕМА 6. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
где слагаемые в правой части определяются соответственно формулами (18.57) и (18.58). Поясним сказанное в этом пункте на примере. Пример 5. Совокупность состоит из двух следующих групп:
Найти групповые, внутригрупповую, межгрупповую и общую дисперсии. Решение. Объемы групп соответственно равны N1 = 10 и N2 = 5. Общий объем совокупности: п = 10 + 5 = 15. Найдем групповые средние:
Теперь находим групповые дисперсии по формуле (18.56):
Внутригрупповая дисперсия, согласно формуле (18.57), равна:
Теперь найдем межгрупповую дисперсию по формуле (18.58), для чего сначала определим общую среднюю:
Наконец, общая дисперсия, согласно формуле (18.59), равна:
Эмпирические моменты
Для вычисления сводных характеристик выборок используют эмпирические моменты, аналогичные соответствующим теоретическим моментам. Обычным эмпирическим моментом порядка s называется среднее значение s-x степеней разностей xi — С, где xi — наблюдаемая варианта, С — произвольная постоянная (ложный нуль — либо мода, либо любая варианта, расположенная примерно в середине вариационного ряда):
При C = 0 имеем начальные эмпирические моменты порядка s; в частности, в случае s = 1
Центральным эмпирическим моментом порядка s называется обычный момент (18.60) при С =
В частности,
Иными словами, выборочная дисперсия равна центральному эмпирическому моменту второго порядка. Центральные моменты выражаются через обычные по формулам, полностью аналогичным (18.19) и (18.20).
Поиск по сайту: |
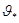 , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру 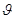 при любой выборке:
при любой выборке:
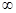 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.








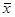 в:
в:


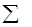 ni, — объем j-й группы.
ni, — объем j-й группы.
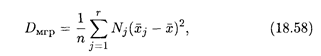
 — объем всей совокупности.
— объем всей совокупности.