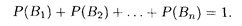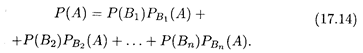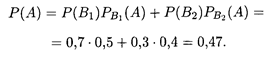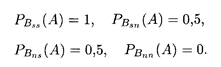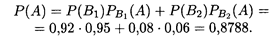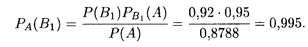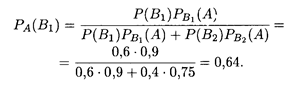Формула полной вероятности

Пусть события В₁, В₂, …, В_п несовместны и образуют пол­ную группу, т.е., согласно теореме 17.2, выполняется ра­венство

Пусть также событие А может наступить при условии появле­ния одного из событий В_i, причем известны как вероятности P(B_i), так и условные вероятности P_Bi(A) (i = 1, 2, ... , п). В таком случае формула для вероятности события А определя­ется следующей теоремой.

ТЕОРЕМА 6. Вероятность события А, появление которо­го возможно лишь при наступлении одного из несовместных событий B_i, образующих полную группу (i = 1, 2, ... ,п), рав­на сумме попарных произведений каждого из этих событий на соответствующую условную вероятность появления со­бытия А:

Пример 3. В двух урнах находятся белые и красные шары: в первой — 4 белых и 5 красных, во второй — 7 белых и 3 красных. Из второй урны наудачу взяли шар и переложили его в первую урну. Найти вероятность того, что наудачу взятый после этого из первой урны шар будет белым.

Решение. Перекладывание из второй урны в первую бело­го шара (событие В₁) и красного шара (событие В₂) образует полную группу независимых событий. Их вероятности соот­ветственно P(B₁) = 0,7 и Р(В₂) = 0,3. Условные вероятнос­ти извлечения из первой урны белого шара (событие А) при добавлении туда белого или красного шара из второй урны соответственно равны Р_B1(А) = 0,5 и Р_B2(А) = 0,4. Искомая вероятность находится по формуле (17.14) при п = 2:

Пример 4. В двух ящиках находятся детали: в первом — 10 штук и из них 3 нестандартные, а во втором — 20 штук и из них 8 нестандартных. Из каждого ящика наудачу вынуто по одной детали, а потом из этих двух деталей наудачу взята одна. Найти вероятность того, что эта деталь окажется стандартной.

Решение. При первой выборке двух деталей возможны четыре случая, которые образуют полную группу независи­мых событий. События B_ss, B_sn, B_ns, B_nn соответствуют случаям изъятия: из первого и второго ящиков по стандарт­ной детали, из первого ящика — стандартной и из второ­го — нестандартной деталей, из первого ящика — нестан­дартной и из второго — стандартной, из первого и второго ящиков по нестандартной детали. В свою очередь события В_ik (i, k = s, n) представляют собой произведения независимых событий — изъятия из каждого ящика по детали, и потому их вероятности равны соответствующим произведениям веро­ятностей этих изъятий: P(B_ss) = 0,7 • 0,6 = 0,42; P(B_sn) = 0,7 • 0,4 = 0,28; P(B_ns) = 0,3 • 0,6 = 0,18; P(B_nn) = 0,3 • 0,4 = 0,12. Условные вероятности выборки из двух деталей стан­дартной, согласно перечисленным выше возможным случаям, равны:

Теперь, согласно теореме 17.6 и формуле (17.14), получаем ис­комую вероятность события А:

Формулы Байеса

Пусть события B₁, B₂, ..., В_п несовместны и образуют пол­ную группу, а событие А может наступить при условии появле­ния одного из них. События B_i называют гипотезами, так как заранее неизвестно, какое из них наступит. Пусть произведено испытание и в результате появилось событие А. Тогда оказывается возможным определить условные вероятности гипотез B_i по следующим формулам:

Формулы (17.15) называются формулами Байеса, по имени их автора. Они позволяют оценить вероятность гипотезы В_i во всех испытаниях, где наступает событие А. Иными слова­ми, зная вероятность Р(В_i) до проведения испытания, мы мо­жем переоценить ее после проведения испытания, в результате которого появилось событие А.

Пример 5. Вероятность изготовления изделия с браком равна 0,08. После изготовления все изделия подвергаются проверке, в результате которой изделия без брака признаются годными с вероятностью 0,95, а изделия с браком — с вероятностью 0,06. Найти долю изделий, выпущенных после проверки, а так­же вероятность того, что выпущенное после проверки изделие окажется без брака.

Решение. Независимые события (гипотезы), образующие полную группу, — это B₁ (изделие без брака) и В₂ (изделие с браком). Пусть событие А заключается в том, что при проверке изделие признается годным. Ответ на первый вопрос задачи дает формула (17.14):

Следовательно, после проверки признаются годными около 88% всех изготовленных изделий.

Ответ на второй вопрос задачи дает формула Байеса (17.15) при п = 2 и i = 1:

Иными словами, среди изделий, прошедших проверку, содер­жится 99, 5% изделий без брака.

Пример 6. В среднем из каждых 100 клиентов отделения бан­ка 60 обслуживаются первым операционистом и 40 — вторым операционистом. Вероятность того, что клиент будет обслужен без помощи заведующего отделением, только самим операци­онистом, составляет 0,9 и 0,75 соответственно для первого и второго служащих банка. Найти вероятность полного обслу­живания клиента первым операционистом.

Решение. Вероятность того, что клиент попадет к перво­му операционисту (событие B₁), составляет 0,6, ко второму — 0,4 (событие В₂). Искомая вероятность полного обслуживания клиента первым операционистом (событие А) определяется по формулам (17.14) и (17.15):

Иными словами, 64% клиентов, попавших на обслуживание к первому операционисту, будут обслужены им полностью.

Поиск по сайту: