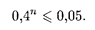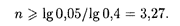|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Произведение событий и условная вероятность
Определение 1. Произведением двух событий А и В называется событие АВ, означающее совместное появление этих событий (см. гл. 1.1, произведение множеств). Например, если событие А — шар, событие В — белый цвет, то их произведение АВ — белый шар. Аналогично определяется произведение нескольких событий, как совместное появление их всех. Если при вычислении вероятности события никаких других ограничений кроме необходимого комплекса условий S не налагается, то такая вероятность называется безусловной. Если же налагаются другие дополнительные условия, содержащие случайные события, то вероятность такого события называется условной. Определение 2. Вероятность события В в предположении о наличии события А называют условной вероятностью РA(В). Пример 1. В ящике лежит 11 деталей, 3 из них нестандартные. Из ящика дважды берут по одной детали, не возвращая их обратно. Найти вероятность того, что во второй раз из ящика будет извлечена стандартная деталь — событие В, если в первый раз была извлечена нестандартная деталь — событие А. Решение. После первого извлечения в ящике из 10 деталей осталось 8 стандартных, и, следовательно, искомая вероятность
Пусть теперь известны вероятность Р(А) события А и условная вероятность РА(В) события В. Тогда справедлива следующая теорема. ТЕОРЕМА 3. Вероятность произведения двух событий определяется формулой
Пример 2. В условиях примера 1 найти вероятности того, что в первый раз извлечена нестандартная деталь, а во второй раз — стандартная, и наоборот. Решение. Итак, событие А — это извлечение из ящика нестандартной детали, а событие В — стандартной. Тогда возможны два случая. 1) Вероятность Р(А) = 3/11, а условная вероятность РA(В) = 0,8. Искомая вероятность произведения этих событий (их совместного появления в указанном порядке) равна, согласно теореме 17.3,
2) Вероятность Р(В) = 8/11, а условная вероятность РB(А) = 0,3. Мы видим, что и в этом случае вероятность произведения событий Р(ВА) = Р(В)РB(А) ≈ 0,22. В этом примере мы проверили известное в теории равенство
Теорема 17.3 допускает обобщение на случай произведения любого числа событий A1, А2, А3, ..., An:
т.е. вероятность совместного появления п событий равна произведению п вероятностей, где PA1A2...Ak-1(Ak) — условные вероятности событий Ak в предположении, что события A1A2 ... Ak-1 уже произошли (k = 1, 2, ... , п). Пример 3. В урне находится 4 белых шара, 5 красных и 3 синих. Наудачу извлекают по одному шару, не возвращая его обратно. Найти вероятность того, что в первый раз появится белый шар (событие А), во второй раз — красный (событие В), в третий — синий (событие С). Решение. Вероятность появления белого шара в первом извлечении Р(А) = 1/3; условная вероятность появления красного шара во втором извлечении при условии появления в первый раз белого шара РA(В) = 5/11; условная вероятность появления синего шара в третьем извлечении при условиях появления в предыдущих извлечениях белого и красного шаров РAB(С) = 0,3. Искомая вероятность определяется по формуле (17.6) при п = 3:
Независимые события Определение 3. Событие В называется независимым от события А, если условная вероятность события В равна его безусловной вероятности (появление события А не влияет на вероятность события В):
Отсюда следует, что и событие А также независимо от события В:
Для независимых событий теорема умножения вероятностей 17.3 в общей форме, которая следует из (17.6), имеет вид
Равенство (17.7) принимается за определение независимых событий. При этом если события независимы, то независимы также и соответствующие им противоположные события. Пример 4. Найти вероятность поражения цели при совместной стрельбе тремя орудиями, если вероятности поражения цели орудиями соответственно равны 0,9, 0,8 и 0,7 (события А, B и С). Решение. Поскольку события А, В и С являются независимыми, то искомая вероятность вычисляется, согласно формуле (17.7), при n = 3:
Когда в результате испытания может иметь место n независимых событий с известными вероятностями их появления, особый интерес представляет случай нахождения вероятности наступления хотя бы одного из них (например, в случае трех событий найти вероятность наступления либо одного, либо двух, либо трех событий). Обозначим это событие через А. Справедлива следующая теорема. ТЕОРЕМА 4. Вероятность появления хотя бы одного из независимых событий А1, A2, ... , Аn определяется формулой
где qi = 1 — pi — вероятности соответствующих противоположных событий В частном случае, когда все события Аi имеют одинаковую вероятность р, из формулы (17.8) следует, что
Пример 5. В условиях примера 4 найти вероятность поражения цели (хотя бы одного попадания) при залповой стрельбе орудий. Решение. Вероятности противоположных событий (промахов) соответственно равны q1 = 0,1, q2 = 0,2, q3 = 0,3. Искомая вероятность находится по формуле (17.8) при п = 3:
Из этого примера наглядно видно преимущество совместного воздействия случайных событий с целью достижения общего результата. Пример 6. На перевозку груза направлены 4 автомобиля. Вероятность нахождения каждой из машин в исправном состоянии равна 0,8. Найти вероятность того, что в работе участвует хотя бы один из выделенных для этого автомобилей. Решение. Вероятность противоположного события (машина неисправна) равна q = 1 - 0,8 = 0,2. По формуле (17.9) находим искомую вероятность при n = 4:
Пример 7. Вероятность обслуживания клиента одним операционистом в банке равна 0,6. Какое минимальное число операционистов должно работать в банке, чтобы вероятность обслуживания клиента была не менее 0,95? Решение. Вероятность противоположного события (отказ в обслуживании клиента операционистом) равна 0,4. Пусть n — количество операционистов, удовлетворяющее условию задачи, т.е.
Решая это неравенство, получаем
Логарифмирование обеих частей этого неравенства дает
Поскольку n должно быть целым числом, окончательно получаем, что в банке должны работать не менее 4 операционистов.
Поиск по сайту: |




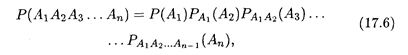






 i (i = 1, 2,... , n).
i (i = 1, 2,... , n).