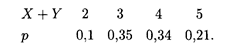|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Двумерная случайная величина
До сих пор мы рассматривали дискретные случайные величины, которые называют одномерными: их возможные значения определялись одним числом. Кроме одномерных величин рассматривают также величины, возможные значения которых определяются несколькими числами. Двумерную случайную величину обозначают через (X, Y); каждая из величин X и Y называется компонентой (составляющей). Обе величины Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Например, при штамповке стальных пластинок их длина и ширина представляют собой двумерную случайную величину. Определение 1. Законом распределения двумерной случайной величины (X, Y) называют множество возможных пар чисел (xi, yj) и их вероятностей p(xi, yj). Двумерную случайную величину можно трактовать как случайную точку А(Х, Y) на координатной плоскости.
Закон распределения двумерной случайной величины обычно задается в виде таблицы, в строках которой указаны возможные значения xi случайной величины X, а в столбцах — возможные значения yj случайной величины Y, на пересечениях строк и столбцов указаны соответствующие вероятности pij. Пусть случайная величина Х может принимать п значений, а случайная величина Y - т значений. Тогда закон распределения двумерной случайной величины (X, Y) имеет вид
Из этой таблицы можно найти законы распределения каждой из случайных компонент. Например, вероятность того, что случайная величина Х примет значение хk, равна, согласно теореме сложения вероятностей независимых событий,
Иными словами, для нахождения вероятности Р(хk) нужно просуммировать все т вероятностей по k-му столбцу таблицы (18.21). Аналогично получается вероятность того, что случайная величина Y примет возможное значение уr: Р(уr) получается суммированием всех n вероятностей r-й строки таблицы (18.21) (r = 1, 2, ... ,m). Отсюда следует, что сумма всех вероятностей в законе распределения (18.21) равна единице:
Пример 1. Задано распределение двумерной случайной величины:
Найти распределения Х, Y и Х + Y. Решение. В нашем случае возможные значения случайной величины X: х1 = 1, х2 = 2, x3 = 3. Тогда, согласно формуле (18.22), имеем P(x1) = 0,1 + 0,2 = 0,3, P(x2) = 0,15 + 0,22 = 0,37, Р(x3) = 0,12 + 0,21 = 0,33. Отсюда получаем закон распределения X:
Аналогично получаем и для распределения Y: у1 = 1, y2 = 2; P(y1) = 0,1 + 0,15 + 0,12 = 0,37, P(y2) = 0,2 + 0,22 + 0,21 = 0,63;
Теперь найдем распределение X+Y. Возможные значения этой случайной величины: 2, 3, 4 и 5. Соответствующие вероятности Р(2) = 0,1, Р(3) = 0,15 + 0,2 = 0,35, Р(4) = 0,12 + 0,22 = 0,34, Р(5) = 0,21. Отсюда находим искомое распределение:
В случае системы двух случайных величин используются кроме математических ожиданий и дисперсий еще и другие числовые характеристики, описывающие их взаимосвязь. Корреляционный момент Определение 2. Корреляционным моментом случайных величин Х и Y (или ковариацией) называется математическое ожидание произведений их отклонений:
Корреляционный момент служит для описания связи между случайными величинами Х и Y. Из свойств математического ожидания легко убедиться в том, что μxy можно записать в следующем виде:
Для непосредственного вычисления корреляционного момента (ковариации) используется формула (см. распределение (18.21))
ТЕОРЕМА 3. Корреляционный момент двух независимых случайных величин Х и Y равен нулю. Если корреляционный момент μxу не равен нулю, то, стало быть, величины Х и Y являются зависимыми.
Поиск по сайту: |