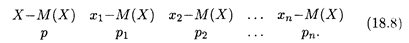Дисперсия дискретной случайной величины

Как уже говорилось выше, математическое ожидание яв­ляется средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые ха­рактеристики. Пусть Х — случайная величина, а М(Х) — ее математическое ожидание.

Определение 2. Разность между случайной величиной и ее математическим ожиданием называется отклонением.

Пусть закон распределения случайной величины Х дается формулой (18.1), тогда отклонение X - M(X) имеет следующий закон распределения:

Отклонение имеет важное свойство, которое устанавливается непосредственно из свойств математического ожидания:

т.е. математическое ожидание отклонения равно нулю.

Пример 5. По данным примера 3 найти закон распределения отклонения числа проданных за день автомашин.

Решение. Как было подсчитано в примере 3, М(Х) = 2,675. Тогда, согласно (18.8), искомый закон определяется следующей таблицей:

На практике важной характеристикой является рассеяние возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, соглас­но (18.9), равно нулю, так как суммируются отрицательные и положительные отклонения (см. пример 5), поэтому целесооб­разно ввести в рассмотрение абсолютные значения отклонений или их квадраты.

Определение 3. Математическое ожидание квадрата откло­нения называется дисперсией, или рассеянием:

Пусть случайная величина задана законом распределения (18.1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения:

Отсюда, согласно формуле (18.10), получаем формулу диспер­сии в развернутом виде:

При вычислении дисперсии часто бывает удобно воспользо­ваться формулой, которая непосредственно выводится из фор­мулы (18.10):

Пример 6. Найти дисперсию ежедневной продажи числа ав­томашин по данным примера 3.

Решение. Закон распределения случайной величины X² имеет вид

Математическое ожидание М(Х²) подсчитывается из этой таб­лицы:

Математическое ожидание М(Х) = 2,675. Следовательно, со­гласно формуле (18.11), получаем искомую величину диспер­сии:

Свойства дисперсии

Приведем здесь основные свойства дисперсии.

Свойство 1. Дисперсия постоянной величины С равна нулю:

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

Свойство 3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:

Перечисленные свойства дисперсии используются при вы­числениях, когда мы имеем дело с несколькими случайными ве­личинами. Из свойств 1 и 3 следует важный вывод: D(X + C) = D(X), где С — постоянная величина. Кроме того, справед­лива следующая теорема.

ТЕОРЕМА 2. Дисперсия числа появления события А в п не­зависимых испытаниях с вероятностью появления р в каж­дом из них этого события вычисляется по формуле

Приведем здесь еще два важных результата: для случай­ной величины, распределенной по закону Пуассона (18.4), ма­тематическое ожидание и дисперсия равны параметру данного распределения.

Пример 7. Найти дисперсию числа выигрышных лотерейных билетов по данным примера 4.

Решение. Имеем 200 независимых испытаний с вероятнос­тью появления выигрышного билета р = 0,015. Стало быть, q = 1 - 0,015 = 0,985, откуда и получаем искомую дисперсию:

Пример 8. Банк выдал ссуды п разным заемщикам в размере S р. каждому под ставку ссудного процента r. Найти матема­тическое ожидание и дисперсию прибыли банка, а также усло­вие на ставку ссудного процента, если вероятность возврата ссуды заемщиком равна р.

Решение. Поскольку заемщики между собой не связаны, то можно полагать, что мы имеем п независимых испытаний. Вероятность утери ссуды для банка в каждом испытании рав­на q = 1 - р. Пусть Х — число заемщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется фор­мулой

где Х является случайной величиной с биномиальным зако­ном распределения. Тогда, согласно теореме 18.1, математи­ческое ожидание прибыли определяется с использованием фор­мулы (18.7):

Поскольку выдача ссуды имеет смысл лишь при положитель­ном математическом ожидании прибыли (положительная сред­няя величина прибыли), то из условия М(П) > 0 вытекает условие на ставку ссудного процента:

Дисперсия прибыли банка находится, согласно теореме 18.2, с использованием формулы (18.14) и свойств 1-3:

Поиск по сайту: