 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическая модель прямых измерений
Классическая математика учит действиям над числами, которые заданы точно, тогда как в подавляющем большинстве случаев, величины, с которыми приходится иметь дело на практике, получают с помощью измерений и потому соответствующие им числа лишь приближенно выражают точные, но неизвестные нам значения реальных величин. Для повышения их точности стремятся сделать как можно больше измерений. Итак, требуется как можно лучше оценить «истинное значение» некоторой величины х, для чего проводится n прямых измерений, результаты которых x1, x2, … xk, … xn, где Используя всю имеющуюся экспериментальную информацию, найдем среднее арифметическое значение, тогда получим
Укажем практическую оценку среднего арифметического (7.1) по числу значащих цифр. Самый простой способ состоит в сравнении среднего арифметического с результатами отдельных измерений. Среднее значение округляют, сохраняя слева все цифры, остающиеся неизменными или почти неизменными во всех отдельных измерениях, а все остальные отбрасываются. Рассмотрим пример: пусть неизвестная величина измерена пять раз [Энциклопедия элементарной математики. – М.;Л.: Гостехиздат; 1951. – Т.1. – С. 385]: х1 = 4,781; х2 = 4,795; х3 = 4,769; х4 = 4,792; х5 = 4,779, среднее арифметическое которых равно 4,7832. Возникает вопрос: какие цифры найденного среднего следует сохранить? Цифра 4 целых в среднем арифметическом значении и во всех результатах отдельных измерений совпадает и должна быть сохранена, как надёжная. То же самое относится и к цифре 7, находящейся в разряде десятых. Цифра 8 в разряде сотых среднего арифметического незначительно отличается от цифр сотых отдельных измерений и сохраняется как значащая. Остальные отбрасываются. Итак, ответ с точностью до трёх значащих цифр: х = 4,78. Теперь рассмотрим так называемый метод наименьших квадратов оценки «истинного значения» некоторой величины х, для чего проводятся n прямых измерений, результаты которых представлены системой уравнений:
По методу наименьших квадратов наилучшим приближенным значением для х является такое число, для которого минимальна сумма квадратов отклонений от
Для определения точки экстремума этой функции, как обычно, находим производную и приравниваем её к нулю
поскольку Итак, модель (7.1) показывает, что в рассматриваемом случае метод наименьших квадратов и выбор среднего арифметического значения результатов прямых измерений приводят к одинаковым результатам, что служит подтверждением практической полезности метода наименьших квадратов, который широко используется при косвенных измерениях.
Поиск по сайту: |
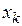результат 
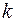-го измерения, a xn – n - го измерения. 
. (7.1)
- результаты измерений, а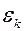 
- их ошибки.
. (7.2)
, откуда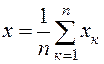
, (7.3)
– квадратный трёхчлен относительно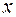 
и 
, то в точке экстремума функция достигает наименьшего значения.