 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Об оценке точности решения
Для выяснения точности решения задачи в простых случаях могут использоваться правила приближенных вычислений. В сложных расчетах, которые проводятся с применением ЭВМ по заданной программе, применять указанные правила не имеет смысла. Здесь можно воспользоваться другим приемом, который продемонстрируем на простых примерах. Вычислить Теперь изменим исходные данные, в рамках их точности, до единицы последнего сохраненного разряда, тогда получим:
Цифра 0 целых во всех трех результатах совпадает и должна быть сохранена, как надёжная. То же самое относится и к цифре 3, находящейся в разряде десятых и к цифре 2 – в разряде сотых. Цифра тысячных в значении Рассмотрим еще менее простое выражение
Рассуждая, как и выше, можно на основании равенства у = 3,859362 с учётом того, что две первые цифры во всех трех результатах совпадают, ответ округлить до у ≈ 3,86. В этих примерах мы использовали максимальные и минимальные в рамках точности значения, однако на практике их трудно находить, да и не нужно. Можно наугад изменять на (+1) или (– 1) последнюю цифру сохраненного разряда каждого исходного данного задачи. Например, запишем
УСТОЙЧИВОСТЬ РЕШЕНИЙ Если математической моделью задачи является система линейных алгебраических уравнений, то следует иметь в виду, что ее коэффициенты имеют конкретный смысл. Они часто получаются в результате измерений и поэтому известны приближенно. Но тогда приходится решать систему, в которой известные величины заданы приближенно. Не так уж редко в таких случаях малые погрешности в исходных данных вызывают достаточно большие погрешности в решениях, которые таким образом оказываются практически непригодными, неустойчивыми, а соответствующие им задачи плохо обусловленными.
Рассмотрим систему уравнений, которую исследовал ещё в 30-х годах прошлого века французский математик Жак Адамар
которая имеет единственное решение:
единственным решением которой будет: Итак, малая погрешность в коэффициенте правой части первого уравнения системы вызывает большие погрешности в решении. Это значит, что решение системы неустойчиво. Теперь обратимся к системе:
Она имеет единственное решение: Как и в предыдущем примере, будем считать все коэффициенты, кроме 39, точными. Заменим в системе (6.2) 39 на 39,1 и решив систему
найдём: х = 15,06, у = 12,02, т.е. малое изменение правой части первого уравнения системы вызывает малые изменения в её решении. Значит, решение системы устойчивое. Конечно, при рассмотрении прикладных задач, важно знать, какое решение найдено: неустойчивое или устойчивое, добротное, которое может быть использовано на практике. Красивую аранжировку текста задачи, решение которой приводит к системе уравнений Жака Адамара, предложил доцент Кемеровского государственного университета культуры и искусств Сорокин А.В.: Для рытья котлована была нанята бригада, состоящая из 10 китайцев и 101 русского. Когда нормировщик произвёл замеры, оказалось, что землекопы вместе вынули за день 111 кубометров грунта. Но работу закончить не успели. Завершить её во второй день поручили одному китайцу и десяти русским, а остальных перебросили на другой объект. Замеры показали, что во второй день было вынуто 11 кубометров грунта. Какова суточная производительность одного китайского землекопа и какова одного русского землекопа, если принять допущение, что у всех китайцев суточная выработка одинакова и у всех русских тоже одинакова? Для решения составим систему уравнений (6.1) с двумя неизвестными (x – суточная выработка китайца, y – суточная выработка русского), которая имеет единственное решение: x = 1,y = 1. То есть китайцы и русские трудились одинаково, вынимая каждый по 1 кубометру грунта в сутки. Но вдруг пришёл нормировщик и сказал, что ошибся. Уточненные замеры показали, что во второй день было вынуто не 11, а 11,1 кубометра грунта, то есть чуть-чуть больше. Казалось бы, на величинах x и y (и, соответственно, на оплате труда) это не должно сильно отразиться. Однако решение системы уравнений показывает, что теперь каждый китаец вынимал в день по 11,1 кубометра грунта, а русские не работали вообще (у= 0)! Итак, решение системы (6.1) – неустойчивое, практически непригодное, поскольку малейшая погрешность (скажем, огрех нормировщика) сводит на нет всё решение. Но, как же, изменить, усовершенствовать систему (6.1), чтобы соответствующее ей решение стало добротным, «прочным», устойчивым? Нетрудно убедиться в том, что для этого достаточно второе уравнение системы (6.1) заменить например на 10х + у = 11, т.е. завершить работу во второй день достаточно было поручить десяти китайцам и одному русскому, а остальных перебросить на другой объект. В этом случае уравнения прямых 10х + у = 11 и 10х + 101у = 111 будут иметь существенно отличающиеся друг от друга угловые коэффициенты, соответственно равные (– 10) и (– 10/101≈ – 0,10). Это свидетельствует о том, что указанные прямые резко отличаются от совпадающих, значит, они имеют одну «прочную» общую точку, соответствующую единственному решению. А прямые системы (6.1) практически совпадают, поскольку их угловые коэффициенты близки друг к другу: (–10/101 ≈ –0,1) и (–1/10 = –0,1). Конечно, для обеспечения устойчивости решения системы (6.1) можно предложить много вариантов замены её второго уравнения. Системы уравнений, приводящие к неустойчивым решениям, в которых небольшие изменения исходных данных приводит к резкому изменению решения, математики называют плохо обусловленными. Тот, кто вздумает применять их на практике, сильно рискует. Ведь если при постройке здания будут использованы решения подобных систем, то будет построено здание, которое окажется неустойчивым к малым колебаниям почвы и наступит катастрофа. Конечно, при рассмотрении прикладных задач, важно знать, какое решение найдено: неустойчивое или устойчивое, добротное, которое может быть использовано на практике. Рассмотрим задачу. Определите молекулярную формулу оксида хлора, если при разложении Решение прикладной задачи, т.е. такой, условие которой содержит нематематические понятия, следует начинать с анализа данных. Так как величины объёмов содержат по одной значащей цифре, да и та в двух случаях равна 1, то достоверность этих данных слишком мала, а потому из условия задачи их лучше удалить, причём в этой задаче без ущерба для дела. Тогда относительная молекулярная масса будет Отметим, что исходные данные задачи получают опытным путём. На эксперименты затрачиваются средства и время: в нашем случае для проведения реакции разложения нужно израсходовать некоторое количество вещества, измерить соответствующие объёмы и привести их к нормальным условиям (н. у.). В рассматриваемом решении эта информация не нужна, поэтому оно эффективнее экономически, да и экологически чище, так как не нужно работать с хлором. Поскольку относительная плотность оксида хлора по воздуху находится экспериментально, её значение 2,34 является приближенным, но, несмотря на это, полученное решение является добротным, устойчивым по отношению к ошибкам в исходных данных: небольшие погрешности измерений не влияют на результат! Действительно, пусть плотность равна 2,3 или 2,4 , тогда правая часть уравнения соответственно будет Теперь рассмотрим задачу. Какая соль и сколько граммов её получится, если для нейтрализации 112 г раствора, содержащего в массовых долях 0,1 гидроксида калия, израсходовали 18 г щавелевой кислоты Её решение, приведенное на с. 140 указанной книги, неустойчиво. Покажем это. Учитывая, что в результате реакции может образоваться как средняя так и кислая соль, запишем неполную схему 0,2 С2Н2О4 + 0,2КОН → х С2К2О4 + у С2КНО4, в которой коэффициенты при исходных веществах взяты равными 0,2, так как количество вещества гидроксида калия
решив которую найдём: х = 0, у = 0,2. Так как n(С2Н2О4) = 18г/90 г/моль = 0,20 моль – осталось без изменения. Теперь неполная схема реакции будет: 0,20 С2Н2О4 + 0,22КОН → х С2К2О4 + у С2КНО4 , а система уравнений примет вид
решая которую находим: х = 0,02, у = 0,18. Итак, в результате реакции в этом случае образуется как кислая, так и средняя соль, т.е. их смесь. Эти расчеты свидетельствуют о том, что рассматриваемая задача плохо обусловлена, а её решение неустойчиво: при малом изменении массовой доли 0,1 резко меняется результат даже качественно, т.е. изменяется и схема реакции, а вместе с ней и состав конечных продуктов. Наука начинается с тех пор, когда начинают измерять. Д.И. Менделеев
Поиск по сайту: |
 . Этот ответ выдает микроЭВМ, но сразу ясно, что большинство цифр в нём сомнительны. По правилам приближенных вычислений результат должен быть округлен до трех значащих цифр, так как наименьшее их количество в компонентах равно трем. Итак, ответ: 0,321, все остальные цифры в записи результата отбрасываются.
. Этот ответ выдает микроЭВМ, но сразу ясно, что большинство цифр в нём сомнительны. По правилам приближенных вычислений результат должен быть округлен до трех значащих цифр, так как наименьшее их количество в компонентах равно трем. Итак, ответ: 0,321, все остальные цифры в записи результата отбрасываются. и
и  .
. на единицу отличается от двух других, поэтому все следующие за тысячными цифры отбрасываются и окончательный результат записывается в виде 0,321, как округленный до тысячных в ответе, выданном ЭВМ для
на единицу отличается от двух других, поэтому все следующие за тысячными цифры отбрасываются и окончательный результат записывается в виде 0,321, как округленный до тысячных в ответе, выданном ЭВМ для 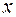 .
. , значение которого сразу выдает микроЭВМ: у = 3,859362. Если пользоваться правилами, то для оценки его точности нужно отдельно знать значения обоих произведений и с их помощью записать ответ: у ≈ 3,86. Однако даже в очень сложных расчетах ЭВМ сразу выдает результат, который можно многократно получать по заданной программе при измененных в пределах точности исходных данных, и по их анализу записывать ответ с соответствующей точностью. Применительно к нашему примеру:
, значение которого сразу выдает микроЭВМ: у = 3,859362. Если пользоваться правилами, то для оценки его точности нужно отдельно знать значения обоих произведений и с их помощью записать ответ: у ≈ 3,86. Однако даже в очень сложных расчетах ЭВМ сразу выдает результат, который можно многократно получать по заданной программе при измененных в пределах точности исходных данных, и по их анализу записывать ответ с соответствующей точностью. Применительно к нашему примеру: ,
, .
.

 , полученные таким путем ук можно усреднить и результат сравнить с
, полученные таким путем ук можно усреднить и результат сравнить с 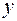 . Для этих целей может быть применен генератор случайных чисел (цифр): при появлении четного значения к последней цифре сохраненного разряда соответствующего исходного данного добавляется единица, в противном случае единица вычитается.
. Для этих целей может быть применен генератор случайных чисел (цифр): при появлении четного значения к последней цифре сохраненного разряда соответствующего исходного данного добавляется единица, в противном случае единица вычитается. (6.1)
(6.1) . Считая в ней все коэффициенты, кроме 11, точными заменим 11 на 11,1, тогда система примет вид
. Считая в ней все коэффициенты, кроме 11, точными заменим 11 на 11,1, тогда система примет вид
 .
. (6.2)
(6.2) .
.
 м3 этого оксида получилось
м3 этого оксида получилось  м3 хлора (н.у.). Относительная плотность этого оксида хлора по воздуху равна 2,34 [34, с.49].
м3 хлора (н.у.). Относительная плотность этого оксида хлора по воздуху равна 2,34 [34, с.49]. . Теперь, записав искомую формулу в виде СlхОу, для определения натуральных чисел
. Теперь, записав искомую формулу в виде СlхОу, для определения натуральных чисел 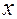 и
и 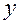 получим уравнение 35,5х + 16у ≈ 67,9, из которого очевидно, что
получим уравнение 35,5х + 16у ≈ 67,9, из которого очевидно, что  и 16у ≈ 67,9 – 35,5 = 32,4. Учитывая, что
и 16у ≈ 67,9 – 35,5 = 32,4. Учитывая, что  – число натуральное, получим у = 2 и СlО2 – формула оксида.
– число натуральное, получим у = 2 и СlО2 – формула оксида. или
или  . Но поскольку
. Но поскольку 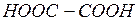 ? (Сергеев С.А. Решения и ответы: К учебнику «Химия»: для 10 – 11 кл. сред. шк. / Рудзитис Г.Е., Фельдман Ф.Г. – Минск: Изд-во «АРТААЛ – ПРЕСС», 1997, С. 139).
? (Сергеев С.А. Решения и ответы: К учебнику «Химия»: для 10 – 11 кл. сред. шк. / Рудзитис Г.Е., Фельдман Ф.Г. – Минск: Изд-во «АРТААЛ – ПРЕСС», 1997, С. 139).
 г)/(56г/моль) = 0,2 моль и
г)/(56г/моль) = 0,2 моль и  (С2Н2О4)= 18г/90 г/моль =0,20 моль, а коэффициенты при продуктах реакции обозначены через
(С2Н2О4)= 18г/90 г/моль =0,20 моль, а коэффициенты при продуктах реакции обозначены через 
 , то средняя соль не образуется. Следовательно, в результате реакции образуется 0,2 моль гидроксалата калия
, то средняя соль не образуется. Следовательно, в результате реакции образуется 0,2 моль гидроксалата калия  или 0,2 моль
или 0,2 моль  г/моль ≈ 0,09 кг (результат округлен до одной значащей цифры). Поскольку в условие входит данное 0,1, достоверность которого весьма мала, решение задачи устойчивым быть не может. Подтвердим это расчётом, заменив 0,1 на 0,11. В этом случае
г/моль ≈ 0,09 кг (результат округлен до одной значащей цифры). Поскольку в условие входит данное 0,1, достоверность которого весьма мала, решение задачи устойчивым быть не может. Подтвердим это расчётом, заменив 0,1 на 0,11. В этом случае 
 =
=  = 0,22 моль,
= 0,22 моль,