 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
О приближенных числах и значащих цифрах
Как правило, решая практические задачи, приходится оперировать приближенными числами, поскольку часто исходные количественные данные получают с помощью измерений и потому соответствующие им числа лишь приближенно выражают точные, но неизвестные нам значения реальных величин. Но и даже тогда, когда нам известны точные значения, например Итак, почти всегда приближенные числа – это и сырье, и продукция реальных вычислений. Даже численность населения большого города – величина приближенная, так как она непрерывно меняется. Яркий образ, помогающий уяснить приближенный характер результата счета количества жителей большого города, приводит И. К. Андронов в книге «Арифметика дробных чисел и основных величин» (М.: Учпедгиз, 1955). «Представим себе, что каждый житель соединен с воображаемым счетчиком так, что каждый родившийся автоматически включается в счетчик, каждый умерший выключается, поднявшийся над городом или выбывший за городскую черту мгновенно выключается, а спустившийся на землю города или прибывший в городскую черту моментально включается в счетчик. Что будет происходить со счетчиком? В оконце счетчика появляются цифры первых 7 разрядов отсчитанного числа.
Что мы будем наблюдать на таком воображаемом счетчике, отражающем численность населения большого города в данный момент? В оконцах VII и VI цифры не изменяются. В оконце V цифры медленно изменяются. В оконце IV цифры меняются быстро. В оконце III цифры меняются так быстро, что их трудно рассмотреть. В оконцах II и I ничего разобрать нельзя, так как цифры меняются с огромной скоростью». Отсюда видно, что уже цифра тысяч (IV оконце) может несколько измениться, пока мы производим запись числа. Поэтому число жителей большого города обычно записывают с точностью до тысяч [8, с. 11]. Значащими цифрами числа в десятичной записи являются все его цифры, кроме нулей, стоящих левее первой, отличной от нуля цифры и нулей, находящихся в конце числа, если они заменяют неизвестные или отброшенные цифры. Подчеркнем, что нули, записанные в конце десятичной дроби, всегда значащие. Например, в числе 5,00 м, полученном в результате измерения с точностью до 1 см, три значащие цифры. А вот нули, стоящие в конце целого числа могут быть как значащими, так и незначащими цифрами. Более того, одни нули могут быть значащими, а другие незначащими. Так, если число 2500 задано с точностью до единиц, оно имеет четыре значащие цифры, если с точностью до десятков – три значащие цифры, при этом самый правый нуль – незначащий. А если это число задано с точностью до сотен, то в нем всего две значащие цифры: 2и5. Если же это число записать в стандартном виде, то по нему сразу видно, сколько значащих цифр в числе: Говоря об округлении целых чисел, отметим, что в 1961 г. в газетах появилось сообщение: население Токио составляет 9 992 542человека [48, с.7]. Ясно одно, что с доверием, по крайней мере к последним четырем цифрам относиться нельзя, так как в таком большом городе колебание населения в несколько тысяч человек в течение одного дня является естественным. Здесь каждая из четырех последних цифр по существу выполняет порядковую функцию, указывая место занимаемого ею разряда, и содержит незначительную, близкую к нулю, количественную информацию. Поэтому каждую цифру с такой функцией естественно считать незначащей и заменить нулем, а результат записать в стандартном виде Напомним, что абсолютная погрешность применяется для сравнения точности значений величин одной размерности и одного порядка, при этом числа записывают так, что предельная абсолютная погрешность не превосходит единицы последнего сохраненного разряда. Для сравнения точности любых приближенных значений используется относительная погрешность. Эта погрешность велика у чисел с одной значащей цифрой, но особенно велика, когда эта цифра равна 1. Если приближенные значения записаны с точностью до единицы последнего разряда числа, то его предельная абсолютная погрешность не превосходит единицы этого разряда. В этих условиях относительная погрешность числа 9 (или 0,9; 0,09 и т.д.) будет Чем больше значащих цифр в числе, тем оно точнее. Для числа 99, Вот этот простейший вычислительный эксперимент показывает, что: «Есть основания не считать значащей цифрой единицу, если она является цифрой старшего разряда приближенного числа, т.е. первой слева его цифрой... Принимая это правило, мы должны, например, число 12,47 считать имеющим не 4, а только 3 значащие цифры» [Энциклопедия элементарной математики, 1951. – с. 379]. Иными словами, если первая слева цифра приближенного числа равна 1, то её лучше не учитывать при подсчете числа его значащих цифр. Следует иметь в виду, что не все значащие цифры имеют в количественном смысле одинаковый «запас значности»: в ряду 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 их «весомость» возрастает. В этой связи рассмотрим задачу: Какова простейшая и молекулярная формула газообразного углеводорода, если массовая доля углерода равна 81,82 % и водорода – 18, 18 %, а Сначала будем решать эту задачу в указанной ниже последовательности в предположении, что все данные точные, предположении столь естественном для классической математики, но не всегда приемлемом на практике. Решение первое. 1. Количество вещества углеводорода объёмом 2. Так как 3. Количество атомов углерода и водорода в молекуле углеводорода соответственно будет Значит, Решение второе. Поскольку Следовательно, Приведенный анализ показывает: формулируя условия прикладной задачи надо иметь в виду, что точности всех исходных данных должны быть согласованы друг с другом и ни одна их них не должна быть недостаточной (да и чрезмерной). Отметим также, что при вычитании двух близких приближенных чисел происходит потеря точности. Например, 528–526=2, т.е. получилось число с одной значащей цифрой. Именно поэтому не следует находить вычитанием массу небольшой навески, взвесив, например, весь реактив вместе с тарой до и после извлечения из неё навески. По той же причине, не имеет смысла находить вычитанием вес шляпы, взвесившись сначала в ней, а затем без нее. По возможности, следует избегать вычитания близких, почти равных приближенных чисел. Например, при решении квадратного уравнения
Поиск по сайту: |
 ,
,  и другие, в реальных вычислениях их округляют.
и другие, в реальных вычислениях их округляют.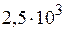 – в числе две значащие цифры, в
– в числе две значащие цифры, в  – три и в
– три и в  – четыре значащие цифры. Это главный аргумент в пользу записи чисел в стандартном виде. Отметим, что в случае округления целых чисел с нулями в конце часто используется и другой способ записи. Вместо:
– четыре значащие цифры. Это главный аргумент в пользу записи чисел в стандартном виде. Отметим, что в случае округления целых чисел с нулями в конце часто используется и другой способ записи. Вместо: 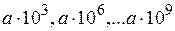 пишут соответственно:
пишут соответственно:  тыс.,
тыс., 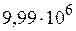 , или, как часто пишут в газетах 10 млн.
, или, как часто пишут в газетах 10 млн. =
= 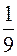 ≈ 0,11 или 11%,
≈ 0,11 или 11%,  = 1 или 100 %. Уже отсюда видно, что предельную относительную погрешность можно принять равной дроби, числитель которой равен 1, а знаменатель – целое число, состоящее из всех значащих цифр, записанных в том порядке, в каком они входят в данное число.
= 1 или 100 %. Уже отсюда видно, что предельную относительную погрешность можно принять равной дроби, числитель которой равен 1, а знаменатель – целое число, состоящее из всех значащих цифр, записанных в том порядке, в каком они входят в данное число. =
=  ≈0,0101, т.е. 1,01 %, а для числа 10,
≈0,0101, т.е. 1,01 %, а для числа 10,  или 10 %, т.е. почти как у числа с одной значащей цифрой, равной 9.
или 10 %, т.е. почти как у числа с одной значащей цифрой, равной 9. м3этого углеводорода (н.у.) имеют массу
м3этого углеводорода (н.у.) имеют массу  кг? [34, с.49].
кг? [34, с.49]. (н.у.) равно 1л : 22,4 л/моль = 0,0446 моль.
(н.у.) равно 1л : 22,4 л/моль = 0,0446 моль.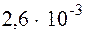 кг = 2,6 г, то молярная масса углеводорода будет 2,6 г : 0,0446 моль = 58 г/моль, т.е. относительная молекулярная масса его 58.
кг = 2,6 г, то молярная масса углеводорода будет 2,6 г : 0,0446 моль = 58 г/моль, т.е. относительная молекулярная масса его 58.
 , т.е.
, т.е.  = 58 - 12 · 4 = 10.
= 58 - 12 · 4 = 10. – молекулярная формула углеводорода (
– молекулярная формула углеводорода (  – простейшая формула).
– простейшая формула). в наименьших целых числах (заметим в скобках:
в наименьших целых числах (заметим в скобках:  ), то
), то  – простейшая формула углеводорода. Итак, два решения и два разных ответа: в первом
– простейшая формула углеводорода. Итак, два решения и два разных ответа: в первом  содержит всего одну значащую цифру, да и ту малозначащую, поскольку она равна 1. Поэтому найденный выше результат
содержит всего одну значащую цифру, да и ту малозначащую, поскольку она равна 1. Поэтому найденный выше результат  не заслуживает никакого доверия. Во втором решении данное 1 л, содержащее одну значащую цифру, не используется.
не заслуживает никакого доверия. Во втором решении данное 1 л, содержащее одну значащую цифру, не используется. – формула углеводорода (молекулярная формула совпадает с простейшей), что подтверждает и проверка. Ответ
– формула углеводорода (молекулярная формула совпадает с простейшей), что подтверждает и проверка. Ответ  в [34], неверный.
в [34], неверный. с приближенными коэффициентами, больший по модулю корень можно находить по обычной формуле, а после этого меньший в особенности при
с приближенными коэффициентами, больший по модулю корень можно находить по обычной формуле, а после этого меньший в особенности при  , из формулы Виета.
, из формулы Виета.