 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Двухкритериальная трактовка риска
Между определенностью и неопределенностью находится случай принятия решения в условиях риска, когда можно оценить вероятность возникновения каждого возможного условия – частичная неопределенность. Широко используемый подход при таких обстоятельствах - критерий предполагаемого выигрыша. Предполагаемый выигрыш рассчитывается для каждой альтернативы, после чего отбирается альтернатива с самым высоким показателем. Предполагаемый выигрыш - это сумма значений выигрыша для каждой альтернативы, причем, каждое значение взвешивается с точки зрения вероятности соответствующего условия. Таким образом, используя критерий предполагаемого выигрыша, можно определить возможное значение выигрыша для каждой альтернативы и выбирать вариант с наилучшим значением выигрыша. В случае стохастической неопределенности, когда неуправляемым факторам (состояниям природы) поставлены в соответствие вероятности, заданные экспертно или вычисленные, решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска. Если для каждой игры с природой, задаваемой платежной матрицей А =
Применительно к матрице рисков (матрице упущенных возможностей (выгод)) лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск:
Когда говорится о среднем выигрыше или риске, то подразумевается многократное повторение процесса принятия решений, хотя реально требуемого количества повторений чаще всего может и не быть. Пример 3.7. Пусть платежная матрица имеет вид:
Определить максимальный средний ожидаемый доход и минимальный средний ожидаемый риск. Решение. По формуле (2.9) строим матрицу рисков R. Находим β1 = max (5, 2, 8, 1) = 8, β2 = 5, β3 = 8, β4 = 12 и тогда
Предположим, что вероятности Р равны: Рj = По формуле (3.11) найдем средний ожидаемый выигрыш:
Максимальный средний ожидаемый доход:
По формуле (3.12) находим средний ожидаемый риск:
Минимальный средний ожидаемый риск:
Покажем, что критерии (3.13) и (3.14) эквивалентны в том смысле, что оптимальные значения для них обеспечивает одна и та же стратегия Аi игрока 1. Действительно,
т.е. значения критериев отличаются на постоянную величину, поэтому принятое решение не зависит от стратегии Аi. Пример 3.8. Для игры, задаваемой матрицей выигрышей
или матрицей рисков
при условии, что Р1 = Р2 = Р3 = Р4 =
Эта же стратегия является лучшей для игрока 1 по критерию (3.14) относительно обеспечения минимального уровня риска:
На практике целесообразно отдавать предпочтение матрице выигрышей или матрице рисков в зависимости от того, какая из них определяется с большей достоверностью. Это особенно важно учитывать при экспертных оценках элементов матриц А и R. Пример 3.9. Имеются два объекта инвестирования с одинаковой прогнозной суммой требуемых капитальных вложений. Величина планируемого дохода (тыс. руб.) в каждом случае неопределенна и приведена в виде распределения вероятностей (таблица 3.7): Таблица 3.7 – Распределение вероятностей получения дохода от объектов инвестирования
Выбрать наиболее предпочтительный проект. Решение. Математические ожидания дохода для рассматриваемых проектов будут соответственно равны: МА = 3000 ∙ 0,10 + 3500 ∙ 0,20 + 4000 ∙ 0,40 + 4500 ∙ 0,20 + 5000 ∙ 0,10 = 4000 тыс. руб. МВ = 4400 тыс. руб. Таким образом, проект В более предпочтителен. В данном случае основным критерием отбора варианта была максимизация математического ожидания дохода. Следует отметить, что этот проект является и относительно более рисковым, поскольку имеет большую вариацию дохода по сравнению с проектом А. Действительно, определяем по формулам (3.2 - 3.4): DA = (3000 – 4000)2 ∙ 0,1 + (3500 – 4000)2 ∙ 0,2 + (4000 – 4000)2 ∙ 0,4 + (4500 – 4000)2 ∙ 0,2 + (5000 – 4000)2 ∙ 0,1 = 300000, σА = DВ = (2000 – 4400)2 ∙ 0,1 + (3000 – 4400)2 ∙ 0,15 + (4000 – 4400)2 ∙ 0,3 + (5000 – 4400)2 ∙ 0,35 + (8000 – 4400)2 ∙ 0,1 = 2340000, σВ = Таким образом, σВ > σА, VB > VA, следовательно проект В является более рискованным. Вероятностная постановка задачи выбора оптимальных решений в экономике более адекватно отображает реальные ситуации. Поэтому применение вероятностных моделей во многих случаях позволяет уменьшить риск при выборе наиболее эффективных решений. Однако применение указанных моделей связано с необходимостью определения вероятностных характеристик анализируемых процессов (ситуаций). Это существенно усложняет решение рассматриваемых задач. Во многих случаях вероятностное распределение экономических показателей бывает неизвестным. Поэтому возникает необходимость определения предпочтительных альтернатив при условии, что вероятностные характеристики экономических показателей являются неизвестными. В условиях полной неопределенности, когда вероятности рассматриваемых ситуаций неизвестны, можно пользоваться правилом Лапласа, заключающимся в том, что все неизвестные вероятности Рj считают равными. После этого выбор эффективного решения можно принимать так же, как и в условиях риска, - по правилу максимизации среднего ожидаемого выигрыша (3.13) или по правилу минимизации среднего ожидаемого риска (3.14). Подобный критерий принятия решения называется принципом недостаточного обоснования Лапласа. Пример 3.10. В условиях полной неопределенности имеются величины потерь при выпуске новых видов продукции
При учете трех вариантов обстановки вероятность каждого варианта составляет 0,33. С использованием принципа недостаточного обоснования Лапласа определить оптимальный вариант решений. Решение. Используя правило минимизации среднего ожидаемого риска, определим: Минимальный средний ожидаемый риск:
Следовательно, в качестве оптимального следует выбирать вариант решения А3.
Поиск по сайту: |
 ,
,  , стратегиям природы Пj соответствуют вероятности Рj, то лучшей стратегией игрока 1 будет та, которая обеспечивает ему максимальный средний выигрыш, т.е.
, стратегиям природы Пj соответствуют вероятности Рj, то лучшей стратегией игрока 1 будет та, которая обеспечивает ему максимальный средний выигрыш, т.е.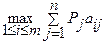 . (3.13)
. (3.13) . (3.14)
. (3.14) .
. .
. .
. = 5 ∙
= 5 ∙  + 2 ∙
+ 2 ∙  + 8 ∙
+ 8 ∙  = 2 ∙
= 2 ∙  = 8 ∙
= 8 ∙  = 1 ∙
= 1 ∙ 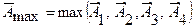 = 6,8.
= 6,8. = 3 ∙
= 3 ∙  = 6 ∙
= 6 ∙  = 0 ∙
= 0 ∙  = 7 ∙
= 7 ∙  1,1.
1,1. (3.15)
(3.15)

 , А1 – лучшая стратегия игрока 1 по критерию (3.13), поскольку
, А1 – лучшая стратегия игрока 1 по критерию (3.13), поскольку
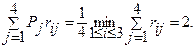
 = 547,7 руб., VА =
= 547,7 руб., VА = 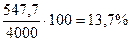 .
.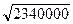 = 1529,7 руб., VB =
= 1529,7 руб., VB =  .
. .
. = 0,55 ∙ 0,33 + 0,47 ∙ 0,33 + 0,00 ∙ 0,33 = 0,3366;
= 0,55 ∙ 0,33 + 0,47 ∙ 0,33 + 0,00 ∙ 0,33 = 0,3366; = 0,05 ∙ 0,33 + 0,62 ∙ 0,33 + 0,10 ∙ 0,33 = 0,2541;
= 0,05 ∙ 0,33 + 0,62 ∙ 0,33 + 0,10 ∙ 0,33 = 0,2541; = 0,45 ∙ 0,33 + 0,00 ∙ 0,33 + 0,20 ∙ 0,33 = 0,2145;
= 0,45 ∙ 0,33 + 0,00 ∙ 0,33 + 0,20 ∙ 0,33 = 0,2145; = 0,00 ∙ 0,33 + 0,72 ∙ 0,33 + 0,05 ∙ 0,33 = 0,2541.
= 0,00 ∙ 0,33 + 0,72 ∙ 0,33 + 0,05 ∙ 0,33 = 0,2541.