 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Критерии эффективности в условиях полной неопределенности
Неопределенность, связанную с отсутствием информации о вероятностях состояний среды (природы), называют «безнадежной» или «дурной». В таких случаях для определения наилучших решений используются следующие критерии: 1. Критерий гарантированного результата (максиминный критерий Вальда) - это пессимистический критерий, потому что принимается во внимание только самый плохой из всех возможных результатов каждой альтернативы. Этот подход устанавливает гарантированный минимум, хотя фактический результат может и не быть настолько плохим. Сущность данного критерия заключается в том, что ЛПР располагает множеством стратегий (вариантов, альтернатив) решения проблемы: А = {Аi}, В качестве Аi могут быть технические параметры проектируемых систем, экономические показатели состояния предприятия, различные варианты решения поставленных задач и т.п. Факторы Пj представляют уровень спроса на товары, предлагаемые фирмой, рыночные цены, условия эксплуатации технических и производственных систем, действия конкурентов и т.д. С позиций данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник. Выбирается решение, для которого достигается значение
Данный критерий обеспечивает максимизацию минимального выигрыша или, что то же самое, минимизацию максимальных потерь, которые могут быть при реализации одной из стратегий. Критерий прост и четок, но консервативен в том смысле, что ориентирует принимающего решение на слишком осторожную линию поведения. Величина, соответствующая максимальному критерию, называется нижней ценой игры, под которой следует понимать максимальный выигрыш, гарантируемый в игре с данным противником выбором одной из своих стратегий при минимальных результатах. Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определяется отношением игрока к риску. Пример 2.7. Предприятие готовится к переходу на новые виды продукции, при этом возможны четыре решения А1, А2, А3, А4, каждому из которых соответствует определенный вид выпуска или их сочетание. Результаты принятия решений существенно зависят от обстановки, которая в значительной мере неопределенна. Варианты обстановки характеризует структура спроса на новую продукцию, которая может быть трех типов: П1, П2, П3. Выигрыш, характеризующий относительную величину результата (доходы, прибыль и т.п.), соответствующий каждой паре сочетаний решений А и обстановки П, представлен в таблице 2.3. Таблица 2.3 - Эффективность выпуска новых видов продукции
Используя максиминный критерий Вальда, найти такую стратегию (линию поведения) Аi, которая по сравнению с другими является наиболее выгодной (оптимальной). Решение. Показатель эффективности по критерию Вальда равен W = и, следовательно, предпочтение необходимо отдать стратегии А1 игрока 1. Выбрав решение А1 независимо от вариантов обстановки получим выигрыш не менее 0,25. При любом другом решении, в случае неблагоприятной обстановки, может быть получен результат (выигрыш) меньше 0,25. Так, при выборе решений А2, полученный выигрыш, в зависимости от наступившего варианта обстановки, будет колебаться от 0,2 до 0,75. Для решений А3 и А4 границы, в которых будет колебаться выигрыш, составят 0,10 ÷ 0,80 и 0,20 ÷ 0,90 соответственно. Данный критерий ориентирует ЛПР на слишком осторожную линию поведения. Этот критерий никак не учитывает, что в случае принятия решения А1 (т.е. при ориентации на выигрыш 0,25), максимальный выигрыш не превышает 0,4. В то время, как выбирая, например, решение А3, при гарантированном выигрыше 0,1 в случае благоприятной обстановки можно получить выигрыш равный 0,80. В ряде экономических задач в качестве критерия эффективности принимаемых решений выступает показатель минимума затрат. В этих ситуациях принцип гарантированных затрат формулируется в виде ЗГ = В качестве затрат З = Пример 2.8. Производится сравнение различных инвестиционных проектов Пр1, Пр2, ... , Прт. Для реализации каждого из проектов необходима определенная величина капитальных вложений К = {Кi}, i = Каждому проекту соответствует определенное значение себестоимости продукции, которую предполагается выпускать при реализации проекта. Совокупность значений себестоимости продукции представляется в виде: C = {Cj}, Каждой паре Кi, Cj соответствует определенное значение приведенных годовых затрат, определяемых по формуле Зij = ЕН ∙ Ki + Cj, (2.12) где ЕН - нормативный коэффициент эффективности капитальных вложений. Располагая наборами {Кi} и {Cj}, составляем матрицу приведенных затрат З = Таблица 2.4 - Зависимость приведенных затрат от величины капитальных вложений (K) и себестоимости продукции (С)
Используя принцип гарантированных затрат, определить наиболее эффективную стратегию вложения средств в инвестиционные проекты. Решение. Критерий гарантированных затрат реализуется как ЗГ = Следовательно, в качестве наиболее эффективной выступает первая стратегия, которой соответствуют капитальные вложения К1. 2. Критерий оптимизма (критерий максимакса) соответствует оптимистической наступательной стратегии, здесь не принимается во внимание никакой возможный результат, кроме самого лучшего. При использовании данного критерия, ЛПР ориентируется на то, что условия функционирования анализируемых систем будут для него наиболее благоприятными. Вследствие этого оптимальным решением является стратегия, приводящая к получению наибольшего значения критерия оптимальности в платежной матрице. Этот критерий целесообразно применять в тех случаях, когда имеется принципиальная возможность повлиять на функции противоположной стороны. С помощью критерия максимакса определяется стратегия, максимизирующая максимальные выигрыши для каждого состояния природы и наилучшим признается решение, при котором достигается максимальный выигрыш, равный
Пример 2.9.Анализируется матрица выпуска новых видов продукции, приведенная в таблице 2.3. Необходимо определить оптимальную стратегию с помощью принципа оптимизма. Решение. В данном случае принцип оптимизма записывается в виде М = что отвечает выбору решения А4. Если рассматривается матрица затрат, то управляемые факторы выбираются так, чтобы минимизировать указанные затраты. Тогда рассматриваемый критерий формируется следующим образом: Зо = Пример 2.10.Рассматривается матрица приведенных годовых затрат, соответствующая таблице 2.4. Необходимо определить наиболее эффективную стратегию, используя критерий оптимизма. Решение. Применительно к рассматриваемой ситуации принцип оптимизма может быть представлен в виде 3o = Следовательно, наиболее эффективной является стратегия, соответствующая К3. Сравнивая два данных решения этого пункта и решения, полученные при использовании критерия гарантированных затрат, получаем, что они не совпадают. Следует ожидать, что такая ситуация будет характерна для большинства анализируемых реальных задач из-за принципиальных отличий критериев. Ситуации, требующие применения критерия оптимизма, в экономике в общем нередки и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение. 3. Критерий пессимизма характеризуется выбором худшей альтернативы из всех худших значений окупаемости. В отличие от критерия оптимизма, когда ЛПР ориентируется на наиболее благоприятную внешнюю среду, которая является неконтролируемой, и на оптимальное использование управляемых факторов, при использовании принципа пессимизма предполагается, что управляемые факторы могут быть использованы неблагоприятным образом Р = Применение этого принципа может вызывать некоторое сомнение, если учесть, что факторы А являются контролируемыми и их следует использовать оптимальным в том или ином смысле образом. Однако в реальных ситуациях в ряде задач может оказаться невозможным контроль за неконтролируемыми факторами, принадлежащими множеству П. Особенно это относится к задачам, связанным с необходимостью учета фактора времени. К этим задачам можно отнести следующие задачи: социально-экономическое прогнозирование; долгосрочное планирование; проектирование сложных объектов и др. Например, издержки производства являются контролируемыми факторами на коротких временных интервалах. Однако, при анализе длительных процессов, которые составляют несколько лет, некоторые элементы указанных издержек становятся неконтролируемыми. К таким элементам можно отнести: стоимость электроэнергии, стоимость материалов и покупных изделий и т.п. Другим примером является определение объемов производства продукции предприятия. Данный показатель также можно считать управляемым фактором. Но он зависит от различных факторов, которые могут существенным образом применяться в процессе производства. При этом указанные факторы относятся к внутренней среде предприятия: уровень конструкторской и технологической подготовки производства, тип используемого оборудования, квалификация работающих и др. Пример 2.11.Компания производит продукцию определенного ассортимента и осуществляет ее сбыт по четырем каналам: • ежемесячный объем продукции с устойчивыми связями по сбыту на ряд лет в среднем составляет 490000 руб.; • ежемесячный объем продукции с устойчивым сбытом, но не на длительный срок - 500000 руб.; • ежемесячный объем продукции обеспечен только разовыми закупками - 510000 руб.; • месячная продукция, покупатель на которую не определен - 480000 руб. Компания может осуществлять производство продукции по трем проектам в объемах 980000 руб., 1500000 руб. и 1980000 руб. В зависимости от изменений рыночной конъюнктуры в связи с имеющимися возможностями реализации рассчитаны варианты среднегодовой прибыли, которые представлены в виде матрицы платежеспособного спроса (таблица 2.5), с учетом ожидаемого значения потерь в случае неудачного исхода, связанных, например, с хранением нереализованной продукции, как следствие неиспользованных возможностей, нерационального распределения инвестиций, снижения оборачиваемости оборотных средств, порчей, либо другими причинами. Таблица 2.5 - Анализ коммерческой стратегии при неопределенной конъюнктуре
При построении платежной матрицы первостепенную важность имеют пропорции исходных и результативных показателей, поскольку вызванные инфляционными пропорциями изменения цен, оказывая влияние на абсолютные величины, не изменяют их пропорциональных соотношений. Это позволяет использовать данную методику в условиях инфляции без дополнительных расчетов. Контролируемыми параметрами являются объем производства и им соответствуют три стратегии А1, А2, А3. Неопределенность Пj связана с колебаниями спроса на продукцию предприятия и ей отвечают четыре стратегии: П1 - низкая зависимость от изменений рыночной конъюнктуры, П2 - средняя зависимость, П3 - зависимость от изменения конъюнктуры высокая, П4 - зависимость от изменений конъюнктуры абсолютная. Требуется, применяя критерий пессимизма, выбрать оптимальную стратегию производства. Решение. Критерий пессимизма равный Р = отвечает стратегии А3, которой соответствует выбор объема производства продукции в сумме 1980000 руб. Для анализа матрицы затрат критерий пессимизма запишется как Зп = Пример 2.12.Располагая матрицей приведенных годовых затрат, представленной в виде таблице 2.4, необходимо выбрать эффективную стратегию с помощью принципа пессимизма. Решение. В рассматриваемой стратегии Зп = Следовательно, затраты Зп = 200 могут быть обеспечены при использовании второй и третьей стратегий. 4. Критерий минимаксного риска Сэвиджа можно рассматривать как критерий наименьшего вреда, который определяет худшие возможные последствия для каждой альтернативы и выбирает альтернативу с лучшим из плохих значений. Выбор стратегии в данном случае аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей А, а матрицей рисков R, построенной по формуле (2.9). Критерий Сэвиджа формулируется следующим образом: S = Пример 2.13.Матрица полезного результата имеет вид, представленный в таблице 2.5. На основе данной матрицы построить матрицу рисков и определить оптимальную стратегию производства с помощью критерия минимаксного риска Сэвиджа. Решение. Найдем значения βj = β1 = β2 = β3 = β4 = а затем по формуле (2.9) строим матрицу рисков (таблица 2.6). Таблица 2.6 - Анализ коммерческого риска при неопределенной конъюнктуре
Критерий минимаксного риска Сэвиджа в данном случае равен S = Следовательно, выбирается стратегия А2, при которой величина риска, равная 95800 руб., принимает минимальное значение в самой неблагоприятной ситуации. Сущность этого критерия состоит в стремлении избежать большого риска при выборе решения. В соответствии с этим критерием (таблица 2.5) следует производить продукцию в объеме А2 = 1500000 руб. Таким образом, критерий Сэвиджа минимизирует возможные потери. Основным исходным допущением этого критерия является предположение о том, что на выбор вариантов обстановки оказывают влияние действия разумных противников (природы), интересы которых прямо противоположны интересам ЛПР. Поэтому, если у противников (конкурентов) имеется возможность извлечь какие-либо преимущества, то они это обязательно сделают. Это обстоятельство заставляет ЛПР обеспечить минимизацию потерь вследствие этих действий. 5. Критерий обобщенного максимина (пессимизма - оптимизма) Гурвица позволяет учитывать состояние между крайним пессимизмом и безудержным оптимизмом. В определенных обстоятельствах каждый из этих методов имеет свои достоинства и недостатки, которые могут помочь в выработке решения. В соответствии с этим компромиссным критерием для каждого решения определяется линейная комбинация минимального и максимального выигрышей. HiА = { и предпочтение отдается варианту решения, для которого окажется максимальным показатель HiА т.е. HА = где р – коэффициент пессимизма-оптимизма (0 ≤ р ≤ 1). При р = 0 критерий Гурвица совпадает с максимаксным критерием, т.е. ориентация на предельный риск, так как больший выигрыш сопряжен, как правило, с большим риском. При р = 1 - ориентация на осторожное поведение (критерий Вальда). Значения р между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от конкретной обстановки и склонности к риску ЛПР. Пример 2.14.Анализируется матрица полезного результата, имеющая вид таблицы 2.5. При значении коэффициента пессимизма-оптимизма р = 0,6 найти оптимальную стратегию Аi. Решение. Вычисляем для каждой стратегии линейную комбинацию: H1А = 0,6 ∙ 49300 + (1 - 0,6) ∙ 197200 = 108460, H2А = 0,6 ∙ (- 60) + (1 - 0,6) ∙ 297800 = 119084, H3А = 0,6 ∙ (- 1140) + (1 - 0,6) ∙ 393600 = 156756. Выбираем наибольшее из этих значений: HА = В соответствии с критерием Гурвица средний размер прибыли будет равен 156756 руб. при выборе объема производства А3 = 1980000 руб. Применительно к матрице рисков R критерий Гурвица имеет вид: HR = При р = 0 выбор стратегии игрока 1 осуществляется по условию наименьшего из всех возможных рисков ( Пример 2.15.Рассматривается матрица коммерческого риска, приведенная в таблице 2.6. Необходимо определить оптимальную стратегию с помощью критерия Гурвица. Коэффициент пессимизма-оптимизма р = 0,6. Решение. Вычисляем линейные комбинации: H1R = 0,6 ∙ 196400 + (1 - 0,6) ∙ 0 = 117840, H2R = 0,6 ∙ 95800 + (1 - 0,6) ∙ 0 = 57480, H3R = 0,6 ∙ 101000 + (1 - 0,6) ∙ 0 = 60600. Находим HR = Пример 2.16.Анализируется матрица выпуска новых видов продукции, приведенная в таблице 2.3. Исследовать зависимость HiА от различных значений коэффициента пессимизма-оптимизма р и показать оптимальные решения. Решение. Результаты вычислений по формуле (2.18) сведены в таблицу 2.7. Таблица 2.7 - Значения показателей HiА и HА для различных значений р
Как видим, с изменением коэффициента р изменяется вариант решения, которому следует отдать предпочтение. Сведем все критерии оптимальности в таблицу 2.8. Таблица 2.8 - Таблица коэффициентов оптимальности
При сравнительном анализе критериев эффективности нецелесообразно останавливаться на выборе единственного критерия, так как в ряде случаев это может привести к неоправданным решениям, ведущим к значительным потерям экономического, социального и иного содержания. Поэтому в указанных ситуациях имеется необходимость применения нескольких критериев в совокупности. Наличие нескольких критериев выбора эффективных альтернатив вносит дополнительную неопределенность при принятии наиболее предпочтительных решений. Следовательно, имеет место неопределенность двух видов: 1)неопределенность, обусловленная отсутствием или недостатком информации об анализируемых процессах; 2)неопределенность, причиной которой является наличие нескольких принципов оптимальности. Пусть при выборе эффективных решений при наличии неуправляемых факторов используется множество критериев оптимальности G = {Gi}, Располагая множеством критериев G = {G(А, П)i} Проанализируем решения примеров, приведенных выше. Анализ выпуска новых видов продукции (таблица 2.3) позволяет выделить следующие лучшие стратегии: по критерию гарантированного результата – А1, по критерию оптимизма - А4, по критерию пессимизма – А3, по критерию Сэвиджа - А3, по критерию Гурвица (пессимизма - оптимизма) при р = 0,6 - А4. Поскольку стратегии А3 и А4 фигурируют в качестве оптимальных по два раза, то к практическому применению можно рекомендовать или стратегию А3 или А4. Вместе с тем, стратегия А3 является более осторожной и, скорее всего, ЛПР выберет стратегию А3. Проведем анализ коммерческой стратегии компании при неопределенной конъюнктуре. Исследование матрицы платежеспособного спроса, представленной в таблице 2.5, показывает, что лучшими являются следующие стратегии: по критерию гарантированного результата – А1, по критерию оптимизма - А3, по критерию пессимизма – А3, по критерию Гурвица при р = 0,6 - А3. Так как стратегия А3 повторяется в качестве оптимальной по трем критериям выбора из пяти, то степень ее надежности можно признать достаточно высокой для того, чтобы рекомендовать эту стратегию к практическому применению. При рассмотрении платежных матриц больших размерностей (т + п - большое) можно быстро, не проводя громоздких вычислительных операций, оценить предлагаемые варианты решений и выбрать из них оптимальный. В этом заключается наиболее существенное преимущество теории оптимальных критериев. Также следует отметить, что имеются стандартные программы для персональных компьютеров, с помощью которых можно исследовать платежные матрицы и находить соответствующие критерии оптимальности. Таким образом, в случае отсутствия информации о вероятностях состояния среды теория не дает однозначных и математически строгих рекомендаций по выбору критериев принятия решений. Это объясняется в большей мере не слабостью теории, а неопределенностью, отсутствием информации в рамках самой ситуации. Единственный разумный подход в подобных случаях - попытаться получить дополнительную информацию, например, путем проведения исследований или экспериментов. В отсутствие дополнительной информации принимаемые решения теоретически недостаточно обоснованы и в значительной мере субъективны. Хотя применение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определенной степени является субъективным (вследствие произвольности выбора критерия принятия решения), оно тем не менее создает определенное упорядочение имеющихся в распоряжении ЛПР данных: определяются множество состояний природы, альтернативные решения, выигрыши и потери при различных сочетаниях состояния «среда-решение». Такое упорядочение представлений о проблеме само по себе способствует повышению качества принимаемых решений.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Найдите седловую точку следующей платежной матрицы:
Задание 2. На основе следующей платежной матрицы определите седловую точку:
Задание 3. Найдите седловую точку для платежной матрицы:
Задание 4. Найдите седловую точку следующей платежной матрицы:
Задание 5. Определите максиминную и минимаксную стратегии для платежной матрицы:
Задание 6. Решите аналитически, используя понятие доминирования, игру, определяемую следующей платежной матрицей:
Задание 7. Уменьшите размеры следующей платежной матрицей, используя понятие доминирования:
Задание 8. Решите аналитически, используя понятие доминирования, игру, определяемую следующей платежной матрицей:
Задание 9. Определите нижнюю и верхнюю цены игры, заданной матрицей выигрышей:
Задание 10. Перейдите от матрицы выигрышей к матрице рисков:
Задание 11. Используя понятие доминирования, уменьшите размеры следующей платежной матрицы:
Задание 12. Игра с природой задана матрицей выигрышей:
Найдите оптимальную стратегию игрока 1, используя в качестве априорной информации о поведении природы критерии Вальда, Сэвиджа и Гурвица (р = 0,6). Задание 13. Платежная матрица имеет вид:
Найдите максиминную и минимаксную стратегии для заданной платежной матрицы. Укажите, имеет ли данная матрица игры седловую точку. Задание 14. Определите, имеет ли заданная платежная матрица седловую точку.
Задание 15. Найдите наилучшие стратегии по критериям: максимакса, Вальда, Сэвиджа, Гурвица (применительно к матрице выигрышей коэффициент пессимизма-оптимизма равен 0,2; применительно к матрице рисков коэффициент пессимизма-оптимизма равен 0,4) для следующей платежной матрицы игры с природой:
Задание 16. Дана матрица игры с природой в условиях полной неопределенности:
Проанализируйте оптимальные стратегии игрока 1, используя критерии пессимизма- оптимизма Гурвица применительно к платежной матрице А и матрице рисков R р = 0; 0,5; 1; при этом выделите критерии максимакса, Вальда и Сэвиджа; установите, какую роль играют стратегии ЛПР при р = 0,5. Задание 17. Анализируется матрица выпуска новых видов продукции, приведенная в таблице. Определите оптимальную стратегию с помощью критерия Вальда. Эффективность выпуска новых видов продукции
Задание 18. Анализируется матрица потерь при выпуске новых видов продукции. Определите наиболее выгодную стратегию с помощью критерия Сэвиджа. Величина потерь при выпуске новых видов продукции
Задание 19. На основе матрицы выигрышей определите наиболее выгодную стратегию с помощью критерия Вальда.
Задание 20.На основе матрицы рисков определите наиболее выгодную стратегию с помощью критерия Сэвиджа.
Задание 21. Анализируется матрица полезного результата. При значении коэффициента пессимизма-оптимизма р =
Задание 22. Анализируется матрица коммерческого риска. При значении коэффициента пессимизма-оптимизма р =
Задание 23.На основе матрицы выигрышей определите наиболее выгодную стратегию с помощью критерия максимакса.
Задание 24.На основе матрицы выигрышей определите наиболее выгодную стратегию с помощью критерия Вальда.
Задание 25.С помощью критерия Сэвиджа определите наиболее выгодную стратегию на основе матрицы рисков.
Задание 26. Анализируется матрица выигрышей. При значении коэффициента пессимизма-оптимизма р = 0,5 найдите оптимальную стратегию с помощью критерия Гурвица.
Задание 27. Анализируется матрица рисков. При значении коэффициента пессимизма-оптимизма р = 0,5 найдите оптимальную стратегию с помощью критерия Гурвица.
Задание 28. Используя понятие доминирования, уменьшите размеры следующей платежной матрицы:
Задание 29. Найдите максиминную и минимаксную стратегии для платежной матрицы:
Задание 30. Уменьшите размеры следующей платежной матрицей, используя понятие доминирования:
Задание 31. Определите максиминную и минимаксную стратегии при заданной матрице эффективности:
Задание 32. Определите верхнюю и нижнюю цены при заданной матрице игры и укажите максиминную и минимаксную стратегии:
Задание 33. Найдите максиминную и минимаксную стратегии для платежной матрицы:
Задание 34. Платежная матрица имеет вид:
Определите верхнюю и нижнюю цены для заданной платежной матрицы и укажите максиминную и минимаксную стратегии.
Поиск по сайту: |
 . Указанные стратегии считаются контролируемыми (управляемыми) факторами. Наряду с факторами управляемыми действуют факторы, которые не поддаются контролю. Обозначают их через П = {Пj},
. Указанные стратегии считаются контролируемыми (управляемыми) факторами. Наряду с факторами управляемыми действуют факторы, которые не поддаются контролю. Обозначают их через П = {Пj},  .
. . (2.10)
. (2.10)
 {0,25; 0,20; 0,10; 0,20} = 0,25
{0,25; 0,20; 0,10; 0,20} = 0,25 . (2.11)
. (2.11) могут выступать: капитальные вложения, валовые издержки производства, приведенные годовые затраты и другие показатели.
могут выступать: капитальные вложения, валовые издержки производства, приведенные годовые затраты и другие показатели. , величины Кi являются управляющими (контролируемыми) факторами.
, величины Кi являются управляющими (контролируемыми) факторами. =
= 
 {130; 200; 200; 150} = 130.
{130; 200; 200; 150} = 130. . (2.13)
. (2.13) . (2.14)
. (2.14) . (2.15)
. (2.15)
 {49300; -60; -1140} = - 1140
{49300; -60; -1140} = - 1140 . (2.16)
. (2.16) . (2.17)
. (2.17) :
: {49300; - 60; - 1140} = 49300,
{49300; - 60; - 1140} = 49300,
 },
}, , (2.18)
, (2.18) . (2.19)
. (2.19) ); при р = 1 – по критерию минимаксного риска Сэвиджа.
); при р = 1 – по критерию минимаксного риска Сэвиджа.


 HR =
HR = 
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. , найдите оптимальную стратегию с помощью критерия Гурвица.
, найдите оптимальную стратегию с помощью критерия Гурвица.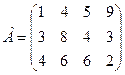 .
. .
. .
. .
. .
. .
. .
. .
. .
.