 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Верхняя и нижняя цена игры
Стратегией игры называется система правил, однозначно определяющих выбор поведения игроков при каждом личном ходе в зависимости от ситуации, которая сложилась в процессе игры. Каждый игрок делает ход в соответствии со своей стратегией, не имея никакой информации о выборе других игроков. Фиксированная стратегия, которую может выбрать игрок, называется его чистой стратегией. В случае, когда участников двое, игра называется прямоугольной. Такая игра задается таблицей (аij)mn, в которой номера строк ( Матрица называется платежной матрицей или матрицей игры, в которой строки соответствуют чистым стратегиям первого игрока, столбцы – чистым стратегиям второго игрока, а компоненты – выигрышу первого игрока при применении каждым из игроков соответствующих чистых стратегий. Рассмотрим матричную игру А =
Имеются пары, в которых каждый из игроков может выбрать чистую стратегию, обеспечивающую ему некоторый максимальный гарантированный выигрыш независимо от поведения противника, причем так, что гарантированные выигрыши игроков различаются только по знаку. Такие игры называются играми, разрешаемыми в чистых стратегиях. Следовательно, игрок 1 стремится принять такую стратегию, которая должна обеспечить максимальный проигрыш игрока 2. Соответственно игрок 2 стремится принять стратегию, обеспечивающую минимальный выигрыш игрока 1. Рассмотрим оба этих подхода. Подход игрока 1. Он должен получить максимальный гарантированный результат при наихудших условиях. Значит, при выборе отвечающей этим условиям своей чистой стратегии он должен выбрать гарантированный результат в наихудших условиях, т.е. наименьшее значение своего выигрыша аij, которое обозначают αi = Чтобы этот гарантированный эффект в наихудших условиях был максимальным, нужно из всех αi выбрать наибольшее значение. Обозначают его α и называют нижней ценой игры (максиминная стратегия): α = Максиминной стратегии отвечает строка матрицы А, которой соответствует элемент α. Какие бы стратегии ни применял игрок 2, игрок 1 максиминной чистой стратегией гарантировал себе выигрыш не меньший, чем α. Таково оптимальное поведение игрока 1. Подход игрока 2. Своими оптимальными стратегиями он стремится уменьшить выигрыш игрока 1, поэтому при каждой j-й чистой стратегии он отыскивает величину своего максимального проигрыша βj = в каждом j-м столбце, т.е. определяет максимальный выигрыш игрока 1, если игрок 2 применит j-ю чистую стратегию. Из всех своих п j-х чистых стратегий он отыскивает такую, при которой игрок 1 получит минимальный выигрыш, т.е. определяет верхнюю цену игры (минимаксная стратегия): β = Верхняя цена игры показывает, какой максимальный выигрыш может гарантировать игрок 1, применяя свои стратегии, - выигрыш, не меньший чем α. Игрок 2 за счет выбора своих чистых стратегий не допустит, чтобы игрок 1 мог получить выигрыш, больший чем β. Таким образом, минимаксная стратегия отображается столбцом платежной матрицы А, в котором находится элемент β. Она является оптимальной чистой гарантирующей стратегией игрока 2, если он ничего не знает о действиях игрока 1. Принцип осторожности, диктующий игрокам выбор стратегий максиминной или минимаксной соответственно, в теории игр именуют принципом «минимакса», а сами стратегии максиминные и минимаксные - общим термином «минимаксные стратегии». Вполне определенной игрой или игрой с седловой точкой называется игра, у которой совпадают нижняя и верхняя цены игры, то есть выполняется равенство: α = При этом V = α = β называется ценой игры, а элемент Простота решения игры с седловой точкой заключается в том, что оптимальные стратегии обоих игроков находятся сразу. Причем, такое решение обладает свойством устойчивости в том смысле, что, если один из игроков применяет свою оптимальную стратегию, то любое отклонение другого игрока от оптимальной стратегии может оказаться не выгодным для него. Пример 2.1. Матрица игры с обозначениями стратегий αi, βj представлена в таблице 2.1. Таблица 2.1 – Матрица игры
Определить верхнюю и нижнюю цены при заданной матрице игры и указать максиминную и минимаксную стратегии. Решение. Определим нижнюю цену игры: α1 = 1; α2 = 4; α = 4 (столбец αi.). Определим верхнюю цену игры: β1 = 4; β2 = 5; β3 = 6; β = 4 (строка βj). Таким образом, α = β = 4, т.е. α = Значит, V = α = β = 4 - цена игры при второй стратегии игрока 1 и первой стратегии игрока 2. Следовательно, имеем игру с седловой точкой. Среди конечных игр, имеющих практическое значение, сравнительно редко встречаются игры с седловой точкой. Более типичным является случай, когда нижняя и верхняя цены игры не совпадают (α ≠ β), причем, в общем случае доказано, что
Пример 2.2. Матрица эффективности приведена в таблице 2.2. Таблица 2.2 – Матрица игры
Определить максиминную и минимаксную стратегии. Решение. Определим максиминную стратегию: α1 = 2; α2 = 4; α = 4. Максиминная стратегия - строка А2. Определим минимаксную стратегию: β1 = 8; β2 = 7; β3 = 9; β4 = 10; β = 7. Минимаксная стратегия - столбец В2. Здесь β > α, следовательно, выполняется условие В игре без седловой точки, если игрок 1 информирован о стратегии, принятой игроком 2, он сможет принять оптимальную стратегию, которая не совпадает с максиминной. Пример 2.3.Дана матрица игры
Допустим, игроку 1 стало известно, что игрок 2 принял минимаксную стратегию. Игрок 1 должен выбрать оптимальную стратегию при условии, что В2 - стратегия игрока 2 (β = 5). Решение. Определим максиминную стратегию игрока 1: α1 = 3; α2 = 4; α = 4. Стратегия игрока 1 - А2 - максиминная. Выберем оптимальную стратегию для игрока 1. Ею будет не максиминная А2, дающая игроку 1 выигрыш α = 4, а та стратегия, которая соответствует Стратегия является оптимальной, если ее применение обеспечит игроку наибольший гарантированный выигрыш при любых возможных стратегиях другого игрока. На примере 2.3 показано, что бывают ситуации, когда игрок 1 может получить выигрыш, превосходящий максиминный, если ему известны намерения игрока 2. Смешанные стратегии Если игра повторяется неоднократно, то постоянное применение минимаксных стратегий становится неразумным. Если игрок 2 будет уверен в том, что на следующем ходу игрок 1 применит прежнюю стратегию, то он несомненно выберет стратегию, отвечающую наименьшему элементу в этой строке, а не прежнюю. Следовательно, при неоднократном повторении игры обоим игрокам следует менять свои стратегии. Тогда возникает вопрос: каким образом их менять, чтобы в среднем выигрыш одного и проигрыш другого был аналогично одноходовой игре, ограничиваясь снизу и сверху соответственно? Для ответа на этот вопрос введем вероятность (относительную частоту) xi применения игроком 1 i-й стратегии, и yj - вероятность применения j-й стратегии игроком 2. Совокупности этих вероятностей определяют векторы X = {x1, х2, …, хт}, где Смешанная стратегия игрока - это полный набор его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Основными условиями применения смешанных стратегий являются: • игра без седловой точки; • игроки используют случайную смесь чистых стратегий с заданными вероятностями; • игра многократно повторяется в сходных условиях; • при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком; • допускается осреднение результатов игр. В частности, решение игры с седловой точкой дается векторами Для получения ограничений на средний выигрыш или проигрыш рассмотрим математическое ожидание выигрыша первого игрока
Если второй игрок выбрал некоторую смешанную стратегию
Аналогично, при выборе первым игроком некоторой стратегии X' второму игроку следует выбирать стратегию
Понятно, что Основная теорема теории игр (доказана фон Нейманом в 1928 году). Каждая матричная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий, то есть существуют стратегии X* и Y*, оптимальные для обоих игроков, причем, max min M (X; Y) = min max M (X; Y) = M (X*; Y*). Число V = M (X*; Y*) называют ценой игры. Из основной теоремы следует, что каждая конечная игра имеет цену, и она лежит между нижней и верхней ценами игры α ≤ V ≤ β. (2.6) И если один из игроков придерживается своей оптимальной стратегии, то выигрыш (проигрыш) его остается неизменным независимо от тактики другого игрока, если, конечно, последний не выходит за пределы своих «полезных» стратегий, иначе выигрыш (проигрыш) возрастает. Это означает выполнение неравенств
(2.7)
Следует отметить, что при выборе оптимальных стратегий игроку 1 всегда будет гарантирован средний выигрыш, не меньший чем цена игры, при любой фиксированной стратегии игрока 2 (и, наоборот, для игрока 2). Активными стратегиями игроков 1 и 2 называют стратегии, входящие в состав оптимальных смешанных стратегий соответствующих игроков с вероятностями, отличными от нуля.
Поиск по сайту: |
 ) отвечают чистым стратегиям второго игрока. Элемент аij интерпретируется как выигрыш первого игрока (проигрыш второго) в случае, если первый игрок использует чистую стратегию i, а второй – чистую стратегию j.
) отвечают чистым стратегиям второго игрока. Элемент аij интерпретируется как выигрыш первого игрока (проигрыш второго) в случае, если первый игрок использует чистую стратегию i, а второй – чистую стратегию j. , представленную матрицей выигрышей m × n, где число строк i =
, представленную матрицей выигрышей m × n, где число строк i =  , а число столбцов j =
, а число столбцов j =  (2.1).
(2.1). . (2.1)
. (2.1) .
. . (2.2)
. (2.2)
 . (2.3)
. (2.3)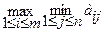 =
=  = β. (2.4)
= β. (2.4) , соответствующий равенству, называется седловой точкой.
, соответствующий равенству, называется седловой точкой.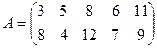 .
. и Y = {y1, y2, …, yn}, где
и Y = {y1, y2, …, yn}, где  . Эти векторы или наборы вероятностей выбора чистых стратегий называются смешанными стратегиями игроков.
. Эти векторы или наборы вероятностей выбора чистых стратегий называются смешанными стратегиями игроков. и
и  , среди компонент которых
, среди компонент которых  , xi = 0 (i ≠ i0) и
, xi = 0 (i ≠ i0) и  , yj = 0 (j ≠ j0).
, yj = 0 (j ≠ j0). . (2.5)
. (2.5)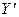 , то первому игроку, естественно, считать лучшей ту смешанную стратегию
, то первому игроку, естественно, считать лучшей ту смешанную стратегию 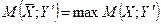 .
. .
.
