 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Доминирование стратегий
Доминирование представляет отношение между стратегиями, наличие которого во многих практических случаях дает возможность сократить размеры исходной платежной матрицы игры. Чистая стратегия аi доминирует над чистой стратегией аk первого игрока, если все элементы i-й строки матрицы игры А (2.1) не меньше соответствующих элементов k-й строки и хотя бы один элемент строго больше. Стратегия аj доминирует над стратегией аl второго игрока, если все элементы j-го столбца матрицы А не больше соответствующих элементов l-го столбца, а хотя бы один элемент строго меньше. Доминирование стратегий можно распространить и на смешанные стратегии. Если элементы одной строки матрицы игры А (2.1) не все меньше (или равны) соответствующих элементов других строк, но все меньше (или равны) некоторых выпуклых линейных комбинаций соответствующих элементов других строк, то эту стратегию можно исключить, заменив ее смешанной стратегией с соответствующими частотами использования чистых стратегий. Аналогично, если каждый элемент некоторого столбца больше или равен некоторой выпуклой линейной комбинации соответствующих элементов некоторых других столбцов, то этот столбец можно исключить из рассмотрения (вычеркнуть из матрицы). Пример 2.4. Используя понятие доминирования, уменьшить размеры следующей платежной матрицы:
Для первых двух чистых стратегий игрока 1 частоты их применения (вероятности) равны 0,25 и 0,75. Решение. Третья стратегия игрока 1 доминируется линейной выпуклой комбинацией первой и второй чистых стратегий, взятых с частотами 0,25 и 0,75 соответственно, т.е. смешанной стратегией: 24 ∙ 0,25 + 0 ∙ 0,75 = 6 > 4; 0 ∙ 0,25 + 8 ∙ 0,75 = 6 > 5. Следовательно, третью стратегию игрока 1 можно исключить, используя вместо нее указанную выше смешанную стратегию. Поэтому исходная матрица игры эквивалентна матрице вида:
Пример 2.5. Уменьшить размеры следующей платежной матрицей, используя понятие доминирования:
Первая и вторая чистые стратегии игрока 2 взяты с частотами 0,5 и 0,5. Решение. Третья стратегия игрока 2 доминируется смешанной стратегией из первой и второй его чистых стратегий: 10 ∙ 0,5 + 0 ∙ 0,5 = 5 < 6; 0 ∙ 0,5 + 10 ∙ 0,5 = 5 < 7. Таким образом, исходная матрица игры эквивалентна матрице следующего вида:
Возможности доминирования смешанными стратегиями в отличие от чистых значительно менее прозрачны (нужно должным образом подобрать частоты применения чистых стратегий), но такие возможности есть. Игры с природой В играх с природой создание модели должно начинаться с построения платежной матрицы. Это наиболее трудоемкий и ответственный этап подготовки принятия решения, так как ошибки в платежной матрице не могут быть компенсированы никакими вычислительными методами и могут привести к неверному итоговому результату. Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком 1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя вполне могут встретиться ситуации, в которых «игроком» 2 действительно может быть природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами). Матрица игры с природой аналогична матрице стратегической игры: А = Доминирование стратегий в игре с природой имеет определенную специфику: исключать из рассмотрения можно лишь доминируемые стратегии игрока 1. Столбцы, отвечающие стратегиям природы, вычеркивать из матрицы игры (исключать из рассмотрения) недопустимо, поскольку природа не стремится к выигрышу в игре с человеком, для нее нет целенаправленно выигрышных или проигрышных стратегий, она действует неосознанно. Методы принятия решений в играх с природой зависят от того, известны или нет вероятности состояний (стратегий) природы, т.е. имеет ли место ситуация риска или неопределенности. Платежная матрица игры с природой (матрица выигрышей игрока 1) имеет вид:
Игрок 1 имеет т возможных стратегий: А1, А2, …, Аm, а у природы имеется п возможных состояний (стратегий) П1, П2, …, Пп. Платит, естественно, не природа, а некая третья сторона (или совокупность сторон, влияющих на принятие решений игроком 1 и объединенных в понятие «природа»). Возможен другой способ задания матрицы игры с природой: не в виде матрицы выигрышей, а в виде матрицы рисков R = Величина риска - это размер платы за отсутствие информации о состоянии среды. Риском rij игрока при использовании им стратегии Аi и при состоянии среды Пj называют разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием среды будет Пj и выигрышем, который игрок получит, не имея этой информации. Зная состояние природы (стратегию) Пj игрок выбирает ту стратегию, при которой его выигрыш максимальный, т.е. rij = βj – aij, (2.9) где βj = Пример 2.6. На основе матрицы выигрышей построить матрицу рисков
Решение. Определим β1 = 4, β2 = 8, β3 = 6, β4 = 9. Согласно введенным определениям rij и βj получаем матрицу рисков
Независимо от вида матрицы игры требуется выбрать такую стратегию игрока (чистую или смешанную, если последняя имеет смысл), которая была бы наиболее выгодной по сравнению с другими. Необходимо отметить, что в игре с природой понятие смешанной стратегии игрока не всегда правомерно, поскольку его действия могут быть альтернативными, т.е. выбор одной из стратегий отвергает все другие стратегии (например, выбор альтернативных проектов). Прежде следует проверить, нет ли среди стратегий игрока доминируемых, и, если таковые имеются, исключить их.
Поиск по сайту: |
 .
. .
. .
.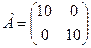 .
. , где аij - выигрыш игрока 1 при реализации его чистой стратегии i и чистой стратегии j игрока 2 (i =
, где аij - выигрыш игрока 1 при реализации его чистой стратегии i и чистой стратегии j игрока 2 (i =  , j =
, j =  ).
). (2.8)
(2.8) или матрицы упущенных возможностей. Матрицу R строят на основе матрицы выигрышей А =
или матрицы упущенных возможностей. Матрицу R строят на основе матрицы выигрышей А =  при заданном j.
при заданном j. .
.