|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Задача 1. Компания «Российский сыр» - небольшой производитель различных продуктов из сыра на экспорт. Один из продуктов - сырная паста - поставляется в страны Ближнего зарубежья. Генеральный директор должен решить, сколько ящиков сырной пасты следует производить в течение месяца. Вероятности того, что спрос на сырную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равны соответственно 0,1; 0,3; 0,5; 0,1. Затраты на производство одного ящика равны 45 долл. Компания продает каждый ящик по цене 95 долл. Если ящик с сырной пастой не продается в течение месяца, то она портится и компания не получает дохода. Сколько ящиков следует производить в течение месяца? Решение. Пользуясь исходными данными, строим матрицу игры. Стратегиями игрока 1 (компания «Российский сыр») являются различные показатели числа ящиков с сырной пастой, которые ему, возможно, следует производить. Состояниями природы выступают величины спроса на аналогичное число ящиков. Вычислим, например, показатель прибыли, которую получит производитель, если он произведет 8 ящиков, а спрос будет только на 7. Каждый ящик продается по 95 долл. Компания продала 7, а произвела 8 ящиков. Следовательно, выручка будет 7 ∙ 95 = 665 долл., а издержки производства 8 ящиков 8 ∙ 45 = 360 долл. Прибыль от указанного сочетания спроса и предложения будет равна П = 7 ∙ 95 - 8 ∙ 45 = 305 долл. Аналогично производятся расчеты при других сочетаниях спроса и предложения. В итоге получим следующую платежную матрицу в игре с природой (таблица 3.12). Таблица 3.12 – Платежная матрица игры с природой
Наибольшая средняя ожидаемая прибыль равна 328,75 долл. Она отвечает производству 8 ящиков. На практике чаще всего в подобных случаях решения принимаются исходя из критерия максимизации средней ожидаемой прибыли или минимизации ожидаемых издержек. Следуя такому подходу, можно остановиться на рекомендации производить 8 ящиков, и для большинства ЛПР рекомендация была бы обоснованной. Однако, привлекая дополнительную информацию в форме расчета среднеквадратического отклонения как индекса риска, можно уточнить принятое на основе максимума прибыли или минимума издержек решение. Дополнительные рекомендации могут оказаться неоднозначными, зависящими от склонности к риску ЛПР. Применим необходимые для наших исследований формулы расчета дисперсии случайной величины и среднеквадратического отклонения. Проводя соответствующие вычисления для случаев производства 6, 7, 8 и 9 ящиков, получаем: 6 ящиков: D = 3002 (0,1 + 0,3 + 0,5 + 0,1) - 3002 = 90000 - 90000 = 0; σ = 0. 7 ящиков: D = (0,1 ∙ 2552 + 0,9 ∙ 3502) – 326,252 = 116752,5 – 106439,06 = 10313,44; σ = 8 ящиков: D = (0,1 ∙ 2102 + 0,3 ∙ 3052 + 0,6 ∙ 4002) – 328,752 = 128317,5 – 108076,56 = 20240,94; σ = 9 ящиков: D = (0,1 ∙ 1652 + 0,3 ∙ 2602 + 0,5 ∙ 3552 + 0,1 ∙ 4502) – 307,52 = 106265 – 94556,25 = 11708,75; σ = Таким образом, из представленных результатов расчетов можно рекомендовать производить 8 ящиков, что вытекает из максимизации прибыли без учета риска. Однако с учетом полученных показателей рисков - среднеквадратических отклонений - очевидно, что при производстве 6 ящиков риск минимальный (σ = 0), но и средняя прибыль в данном случае будет наименьшая в сравнении с вариантами производства 7, 8 или 9 ящиков. Решение о целесообразности производства определенного количества ящиков должен принимать генеральный директор компании «Российский сыр» с учетом его опыта, склонности к риску и степени достоверности показателей вероятностей спроса: 0,1; 0,3; 0,5; 0,1. Задача 2. Необходимо закупить уголь для обогрева дома. Количество хранимого угля ограничено и в течение холодного периода должно быть полностью израсходовано. Предполагается, что неизрасходованный зимой уголь в лето пропадет. Покупать уголь можно в любое время, однако летом он дешевле, чем зимой. Неопределенность состоит в том, что не известно, какой будет зима: суровой, тогда придется докупать уголь, или мягкой, тогда часть угля может остаться неиспользованной. Имеются следующие данные о количестве и ценах угля, необходимого зимой для отопления дома (таблица 3.13). Вероятности зим: мягкой - 0,35; обычной - 0,5; холодной - 0,15. Таблица 3.13 - Данные о количестве и ценах угля для отопления дома зимой
Приведенные цены относятся к покупкам угля зимой. Летом цена угля 6 ф. ст. за 1 т, имеется место для хранения запаса угля до 6 т, заготавливаемого летом. Если потребуется зимой докупить недостающее количество угля, докупка будет по зимним ценам. Предполагается, что весь уголь, который сохранится до конца зимы, в лето пропадет (предположение делается для упрощения постановки и решения задачи). Сколько угля летом покупать на зиму? Решение. Построим платежную матрицу (таблица 3.14). Таблица 3.14 – Платежная матрица
Произведем расчет ожидаемой средней платы за уголь (таблица 3.15). Таблица 3.15 – Средняя ожидаемая плата за уголь
Как видно из таблицы 3.15, наименьшая ожидаемая средняя плата приходится на случай мягкой зимы (30,15 ф. ст.). Соответственно если не учитывать степени риска, то представляется целесообразным летом закупить 4 т угля, а зимой, если потребуется, докупить уголь по более высоким зимним ценам. Если продолжить исследование процесса принятия решения и вычислить среднеквадратические отклонения платы за уголь для мягкой, обычной и холодной зимы, то соответственно получим: • для мягкой зимы σ = 5,357; • для обычной зимы σ = 2,856; • для холодной зимы σ = 0. Минимальный риск, естественно, будет для холодной зимы, однако при этом ожидаемая средняя плата за уголь оказывается максимальной - 36 ф. ст. Следовательно, целесообразно выбрать вариант покупки угля для обычной зимы, так как согласно таблице 3.15 ожидаемая средняя плата за уголь по сравнению с вариантом для мягкой зимы возрастает на 3,5%, а степень риска при этом оказывается почти в 2 раза меньшей (σ = 2,856 против 5,357). Отношение среднеквадратического отклонения к математическому ожиданию - вариабельность (средний риск на затрачиваемый 1 ф. ст.) для обычной зимы составляет Эти соотношения и позволяют рекомендовать покупку угля, ориентируясь не на мягкую, а на обычную зиму. Задача 3. ОАО «Фото и цвет» - небольшой производитель химических реактивов и оборудования, которые используются некоторыми фотостудиями при изготовлении 35-мм фильмов. Один из продуктов, который предлагает ОАО «Фото и цвет», - ВС-6. Президент акционерного общества продает в течение недели 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика предприятие получает 35 тыс. руб. прибыли. Как и многие фотографические реактивы, ВС-6 имеет очень малый срок годности. Поэтому, если ящик не продан к концу недели, он должен быть уничтожен. Каждый ящик обходится предприятию в 56 тыс. руб. Вероятности продать 11, 12 и 13 ящиков в течение недели равны соответственно 0,45; 0,35; 0,2. Как вы советуете поступить? Как вы порекомендуете поступить, если бы ОАО «Фото и цвет» мог сделать ВС-6 с добавкой, значительно продлевающей срок его годности? Решение. Матрицу игры с природой (здесь ОАО «Фото и цвет» - игрок с природой, а природа - торговая конъюнктура) строим следующим образом (таблица 3.16). Таблица 3.16 – Платежная матрица игры с природой
Расчет средней ожидаемой прибыли производится с использованием вероятностей состояний природы. Таким образом, наибольшая из средних ожидаемых прибылей (389,67 тыс. руб.) отвечает при заданных возможностях спроса производству 12 ящиков ВС-6. Производство 12 ящиков в неделю следует рекомендовать ОАО «Фото и цвет», т.к. показатель риска - среднеквадратическое отклонение σ - минимален при максимальной средней ожидаемой прибыли. Если срок службы химического реактива будет удлинен, то его производство даже при прежнем спросе можно увеличить, частично производя на склад для последующей реализации.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Акционерному обществу предлагаются два рисковых проекта:
Определить, какой проект должны выбрать акционеры. Задание 2. Проект А с вероятностью 0,6 обеспечивает прибыль 20 млн. руб., но с вероятностью 0,4 можно потерять 20 млн. млн. руб.; для проекта Б с вероятностью 0,7 можно получить прибыль 10 млн. руб. и с вероятностью 0,3 потерять 10 млн. руб. Выберите наименее рисковый проект. Задание 3. На основе следующих данных рассчитайте коэффициент риска и выберите наименее рисковый вариант вложения капитала. Вариант А. Собственные средства инвестора – 5000 тыс. руб. Максимально возможная сумма убытка – 3500 тыс. руб. Вариант Б. Собственные средства инвестора – 30000 тыс. руб. Максимально возможная сумма убытка – 12000 тыс. руб. Задание 4. На основе следующих данных выберите вариант вложения капитала.
Критерием выбора является наименьшая колеблемость прибыли. Задание 5. При вложении капитала в мероприятие А из 200 случаев прибыль 25 тыс. руб. была получена в 20 случаях, прибыль 30 тыс. руб. была получена в 80 случаях, прибыль 40 тыс. руб. была получена в 100 случаях. При вложении капитала в мероприятие Б из 240 случаев прибыль 30 тыс. руб. была получена в 144 случаях, прибыль 35 тыс. руб. была получена в 72 случаях, прибыль 45 тыс. руб. была получена в 24 случаях. Выберите вариант вложения капитала. Критерием выбора является наибольшая сумма средней прибыли. Задание 6. На основе следующих данных выберите варианты вложения капитала. Норма прибыли на вложенный капитал
Вероятности условий хозяйственных ситуаций составляют: 0,2 – для ситуации А 1; 0,3 – для ситуации А 2; 0,5 – для ситуации А 3. Задание 7. Господин А делает заем под процент i и под залог недвижимости. На полученные взаймы деньги господин А покупает акции. Пусть эффективность R покупаемых господином А акций характеризуется математическим ожиданием дохода М и дисперсией s2, оценивающей рискованность финансовой операции. Найдите, используя неравенство Чебышева, соотношение между i, М, s2, при которой вероятность того, что господин А не сможет вернуть долг и лишится недвижимости меньше или равна 0,04. Задание 8.На основе матрицы рисков и с учетом следующих вероятностей Pj =
Задание 9.На основе матрицы выигрышей и с учетом следующих вероятностей р1 = р2 = р3 = р4 =
Задание 10.На основе матрицы упущенных выгод и с учетом следующих вероятностей р1 = р2 = р3 = р4 =
Задание 11. Определите, в какую из перечисленных акций вложения наиболее рискованны:
Задание 12. Определите, какой из проектов рискованнее:
Задание 13. Из одного города в другой должен перевозиться груз двумя видами транспорта: железнодорожным и автомобильным.
Определите, на каком виде транспорта будет выгоднее перевозить груз. Обоснуйте ответ. Задание 14. Предприятие для реализации товара имеет возможность осуществлять три вида мероприятий.
Определите, при реализации какого мероприятия предприятие получит наибольшую прибыль. Обоснуйте ответ. Задание 15. При продвижении нового товара мероприятие А из 200 случает давало прибыль 20,0 тыс. руб. с каждой единицы товара в 90 случаях (вероятность 90 : 200 = 0,45), прибыль 25,0 тыс. руб. в 60 случаях (вероятность 60 : 200 = 0,30) и прибыль 30,0 тыс. руб. в 50 случаях (вероятность 50 : 200 = 0,25). Осуществление мероприятия Б из 200 случаев давало прибыль 19,0 тыс. руб. в 85 случаях, прибыль 24,0 тыс. руб. в 65 случаях, 31,0 тыс. руб. в 50 случаях. Определите среднее ожидаемое значение прибыли для мероприятий А и Б. Сделайте вывод: от какого мероприятия будет получена наибольшая прибыль. Задание 16. Небольшая частная фирма производит косметическую продукцию для подростков. В течение месяца реализуется 15, 16 или 17 упаковок товара. От продажи каждой упаковки фирма получает 75 руб. прибыли. Косметика имеет малый срок годности, поэтому, если упаковка не продана в месячный срок, она должна быть уничтожена. Поскольку производство одной упаковки обходится в 115 руб., потери фирмы составляют 115 руб., если упаковка не продана к концу месяца. Вероятности продать 15, 16 или 17 упаковок за месяц составляют соответственно 0,55; 0,1 и 0,35. Определите, сколько упаковок косметики следует производить фирме ежемесячно? Какова ожидаемая стоимостная ценность этого решения? Сколько упаковок можно было бы производить при значительном продлении срока хранения косметической продукции? Задание 17. Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7, 8, 9 или 10 бидонов, равны соответственно 0,2; 0,2; 0,5 и 0,1. Покупка одного бидона сметаны обходится магазину в 70 руб., а продается сметана по цене 110 руб. за бидон. Если сметана не продается в течение недели, она портится, и магазин несет убытки. Определите, сколько бидонов сметаны желательно приобретать для продажи? Какова ожидаемая стоимостная ценность этого решения?
ПОЗИЦИОННЫЕ ИГРЫ
Дерево решений Во многих практических важных конфликтных ситуациях стороны-участницы, располагая той или иной информацией о прошлом развитии конфликта, совершают свой выбор не раз и навсегда, а последовательно во времени, шаг за шагом. Тем самым они используют стратегии, отражающие как динамику конфликта, так и степень собственной информированности о фактически складывающейся обстановке в развитии этого конфликта. Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются позиционные игры. Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях, меняющихся во времени (неопределенность, обусловленная неполной информацией). Процесс самой игры состоит в последовательном переходе от одного состояния игры к другому, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом (случайный ход). Состояния игры называют позициями, возможные выборы в каждой позиции – альтернативами. Одноэтапные игры с природой удобно использовать в задачах, имеющих одно множество альтернативных решений и одно множество состояний среды. Позиционные игры, однако, требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий игрока и состояний природы порождает другое состояние подобного типа. Если имеют место два (или более) последовательных множества решений, причем последующие решения основываются на результатах предыдущих, и/или два (или более) множества состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью), используется дерево решений. Дерево решений – это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды. Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение пяти этапов: 1. Формулирование задачи. Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволяет привести описание задачи принятия решения к поддающейся анализу форме. Должны быть выполнены следующие основные процедуры: определение возможности сбора информации для экспериментирования и реальных действий; составление перечня событий, которые с определенной вероятностью могут произойти; установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять. 2. Построение дерева решений. Оно состоит из двух основных частей: «решений» и «вероятностных событий» (рисунок 4.1).
Рисунок 4.1 - Составные части дерева решений 3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Указанные вероятности определяются либо на основании имеющейся статистики, либо экспертным путем. 4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды. 5. Решение задачи. Дерево решений состоит из ряда узлов и исходящих из них ветвей. Квадраты обозначают пункты принятия решений (или возможные события), а дуги соответствуют переходам между логически связанными решениями и случайными событиями. Из вершины-решения (квадратов) исходит столько дуг, сколько имеется вариантов (альтернатив), выбор конкретной дуги (вариант решения) осуществляется ЛПР. Из вершины-события также может исходить несколько дуг. Но здесь уже выбор осуществляется случайным образом в соответствии с заданными вероятностями отдельных исходов. После того, как дерево решения построено, оно анализируется справа налево, т.е. начинать надо с последнего принятого решения. Для каждого решения выбирается альтернатива с наибольшим показателем отдачи (или с наименьшими затратами). Если за принятием решения следует несколько возможных вариантов событий, то выбирается альтернатива с наибольшей предполагаемой прибылью (или с наименьшей предполагаемой величиной затрат). Различают следующие виды позиционных игр: - позиционные игры с полной информацией, в которых каждый игрок при своем ходе знает ту позицию дерева решений, в которой он находится; - позиционные игры с неполной информацией, где игрок, делающий ход, не знает точно, в какой именно позиции дерева решений он фактически находится. Этому игроку известно лишь некоторое множество позиций, включающее в себя его фактическую позицию. Такое множество позиций называется информационным множеством. В зависимости от отношения к риску решение задачи может выполняться с позиции «объективистов» и «субъективистов». Пусть предлагается лотерея: за 10 руб. (стоимость лотерейного билета) игрок с равной вероятностью р = 0,5 может ничего не выиграть или выиграть 100 руб. Один индивид пожалеет и 10 руб. за право участия в такой лотерее, т.е. просто не купит лотерейный билет, другой готов заплатить за лотерейный билет 50 руб., а третей заплатит даже 60 руб. за возможность получить 100 руб. (например, когда ситуация складывается так, что, только имея 100 руб., игрок может достичь своей цели, поэтому возможная потеря последних денежных средств, а у него их росно 60 руб., не меняет для него ситуации). Безусловным денежным эквивалентом (БДЭ) игры называется максимальная сумма денег, которую ЛПР готов заплатить за участие в игре, или, что то же, та минимальная сумма денег, за которую он готов отказаться от игры. Каждый индивид имеет свой БДЭ. Индивида, для которого БДЭ совпадает с ожидаемой денежной оценкой (ОДО) игры, т.е. со средним выигрышем в игре, условно называют объективистом, индивида, для которого БДЭ ≠ ОДО, - субъективистом. Ожидаемая денежная оценка – это средний выигрыш в игре, рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей. Например, для рассмотренной лотереи ОДО = 0,5 ∙ 0 + 0,5 ∙ 100 = 50 руб. Если субъективист склонен к риску, то его БДЭ > ОДО, если не склонен, то БДЭ < ОДО. Предположим, что решения принимаются с позиции объективиста. В постановочном плане рассмотрим несколько задач, которые могут быть решены с помощью данного метода. Пример 4.1. Оптимизация стратегии выхода на рынок Пусть есть фирма А, которая единолично доминирует на рынке некоторого товара, имея 20 единиц прибыли за какой-то интервал. Фирма В хотела бы продавать тот же товар на этом рынке, для чего ей надо произвести какие-то первоначальные затраты. При вторжении фирмы В на рынок фирма А может и не сократить объем своего производства. Тогда на рынке товара будет очень много, цена на него упадет, и прибыли фирм будут: у фирмы А (+8) единиц, у фирмы В (-3) единицы, то есть фирма В понесет убыток. Если фирма А уступит фирме В половину рынка, то прибыли будут по (+10) единиц. Если фирма А, ожидая вступления фирмы В на рынок, сократит производство, а фирма В на рынок не вступит, то прибыль фирмы А будет (+12) единиц. У фирмы В не будет ни расходов, ни доходов, ее прибыль будет нулевой. Позиционную игру представим деревом решений (в общем случае графом решений), которое приводит игроков из исходной позиции в конечную (рисунок 4.2).
Рисунок 4.2 - Схема позиционной игры Можно проверить, что в данной игре есть пары стратегий равновесных по Нэшу (смысл ситуации в том, что никому из игроков в одиночку не выгодно от нее отклоняться, его выигрыш при этом не увеличится): 1)фирма В - воздержаться от вступления на рынок; фирма А - сохранить объем производства; 2)фирма В - вступить на рынок; фирма А - снизить объем производства. Проверка проста, в первом случае она делается так. Пусть фирма В придерживается данной стратегии, а фирма А изменяет свою стратегию. Тогда фирма А вместо выигрыша (+20) единиц получит только (+12). Если фирма А придерживается выбранной стратегии, а фирма В меняет свою стратегию, то она вместо выигрыша (0) единиц получает выигрыш (-3) единицы. Аналогично делается проверка и во втором случае. В непозиционной игре, когда игроки одновременно и независимо принимают решения, нет оснований ожидать, что какой-то из этих двух исходов предпочтительнее. В позиционной игре надо учитывать, что фирма А принимает решение, уже зная о решении фирмы В, которая делает первый ход. Следуя принципу максимизации своего минимального выигрыша, то есть действуя осторожно, фирма В должна воздержаться от вступления на рынок. Но в позиционной игре, когда есть последовательные ходы, ситуация сложнее. Фирма В, конечно, исходит из того, что фирма А будет вести себя рационально, будет стремиться максимизировать свой выигрыш. Рациональным ответом фирмы А на вторжение фирмы В является уменьшение своего производства, так как при этом ее прибыль больше, чем при сохранении прежнего объема выпуска. Поэтому для фирмы В разумно вторгаться на рынок, считая угрозу фирмы А (сохранение ею прежнего объема производства) неправдоподобной. Совсем другое решение будет в том случае, когда дерево решений игры имеет вид, показанный на рисунке 4.3.
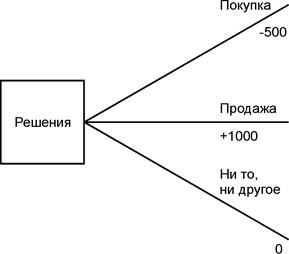
Рисунок 4.3 - Схема позиционной игры В данном случае фирме А не выгодно сократить объем своего производства при любом решении фирмы В. Поэтому угроза фирмы А (сохранить прежний объем производства) становится реальной, и для фирмы В разумным является отказ от вступления на рынок Данная ситуация - случай устойчивой монопо Пример 4.2. Максимизация прибыли от акций Пусть мы владеем акциями стоимостью 1000 руб. Мы должны принять решение относительно того, держать ли акции, продать их все или купить еще акции на сумму 500 руб. Вероятность 20%-го роста курсовой стоимости акции составляет 0,6, а вероятность снижения курсовой стоимости на 20% - 0,4. Какое решение необходимо принять с тем, чтобы максимизировать ожидаемую прибыль? Сначала необходимо решить, что делать с акциями: купить еще, все продать или все держать (рисунок 4.4).
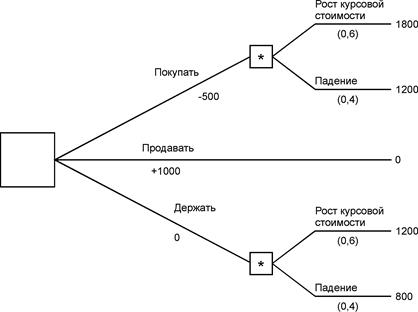
Рисунок 4.4 – Покупать, продавать или ни то, ни другое Диаграмма содержит величину доходов или расходов в случае принятия того или иного решения. Например, вариант «продажи» даст доход в 1000 руб. (показан как + 1000 на дереве). В противоположность этому, вариант «покупки» принесет расходы в сумме 500 руб. (показаны как -500 на дереве) Если мы продадим акции, тогда их у нас будет ноль. Если мы просто будем держать акции, то в случае 20%-ного подъема на рынке их стоимость составит 1200 руб., а в случает 20%-ного спада - 800 руб. В другом случае, после покупки акций еще на 500 руб. при подъеме рынка мы окажемся обладателями акций стоимостью 1800 руб., а при падении - стоимостью 1200 руб. Данные значения указаны в конце каждой ветви в правой части дерева решений (рисунок 4.5).
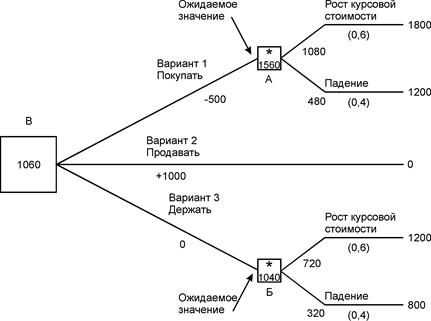
Рисунок 4.5 – Дерево решений Дерево также показывает вероятности возможных событий (т.е. рост или падение курсовой стоимости акций), а также денежные средства, затраченные или полученные при этом. Например, покупка акции стоит 500 руб. (т.е. в данной точке диаграммы указано -500 руб.). Аналогично, продажа акций даст доход в 1000 руб., и это указано рядом с соответствующей ветвью дерева. Начиная с правой стороны и двигаясь влево, производится расчет ожидаемых значений, как это показано на рисунке 4.6.
Рисунок 4.6 – Ожидаемые значения Таким образом, ожидаемое значение в блоке вероятностных событий А рассчитывается путем умножения каждой вероятности на значение в конце ветви, т.е. ожидаемое значение в блоке А составляет 0,6 ∙ 1800 + 0,4 ∙ 1200 = 1560 руб. Аналогично, ожидаемое значение для блока Б составляет 0,6 ∙ 1200 + 0,4 ∙ 800 = 1040 руб. И наконец, можно принимать решение на основании вывода ожидаемых значений по соответствующим ветвям обратно к блоку решений В. Три возможных пути обратно к блоку В дают следующие значения: Вариант 1: 1560 - 500 = 1060 руб. Вариант 2: 0 + 1000 = 1000 руб. Вариант 3: 1040 + 0 = 1040 руб. Следовательно, на основании данного критерия с целью максимизации ожидаемой стоимости акций мы предпочтем вариант 1. Таким образом, мы решим купить еще акций на сумму в 500 руб., что даст нам ожидаемую чистую прибыль в 1060 руб. Это значение показано в блоке В, а путь решения выделен на рисунке 4.6. Следует отметить, что этот простой способ принятия решений, основанный на максимизации ожидаемой отдачи, может не всегда оказаться приемлемым, например, также необходимо учитывать факторы риска. Пример 4.3. Выбор оптимального проекта строительства предприятия Руководство компании решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (таблица 4.1). Таблица 4.1 – Таблица проектов строительства предприятия
Так как истинные вероятности благоприятного и неблагоприятного состояний экономической среды неизвестны, то в соответствии с правилом Лапласа равновозможности принимается наличие состояний с вероятностями 0,5 удачи и 0,5 неудачи. На основе данной таблицы выигрышей (потерь) можно построить дерево решений (рисунок 4.7).

- решение (решение принимает игрок);
// - отвергнутое решение Рисунок 4.7 - Дерево решений без дополнительного обследования конъюнктуры рынка Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ожидаемой денежной оценки. Определим средний ожидаемый выигрыш: •для вершины 1: ОДО1 = 0,5 ∙ 200000 + 0,5 ∙ (-180000) = 10000 руб.; •для вершины 2: ОДО2 = 0,5 ∙ 100000 + 0,5 ∙ (-20000) = 40000 руб.; •для вершины 3:ОДО3= 10000 руб. Таким образом, наиболее целесообразно выбрать стратегию а2, т.е. строить малое предприятие, а ветви (стратегии) а1 и а3 дерева решений можно отбросить. ОДО наилучшего решения равна 40000 руб. Следует отметить, что наличие состояния с вероятностями 50% неудачи и 50% удачи на практике часто означает, что истинные вероятности игроку, скорее всего, неизвестны и он всего лишь принимает такую гипотезу (так называемое предположение «fifty - fifty» - пятьдесят на пятьдесят). Усложним рассмотренную выше задачу. Пусть перед тем как принимать решение о строительстве, руководство компании должно определить, заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая услуга обойдется компании в 10000 руб. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей. Относительно фирмы, которой можно заказать прогноз, известно, что она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в виде условных вероятностей благоприятности и неблагоприятности рынка сбыта представлены в таблице. 4.2. Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73. Таблица 4.2 – Условные вероятности благоприятности и неблагоприятности рынка сбыта фирмы
Предположим, что фирма, которой заказали прогноз состояния рынка, утверждает: • ситуация будет благоприятной с вероятностью 0,45; • ситуация будет неблагоприятной с вероятностью 0,55. На основании дополнительных сведений можно построить новое дерево решений (рисунок 4.8), где развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным.

- решение (решение принимает игрок);
// - отвергнутое решение Рисунок 4.8 - Дерево решений при дополнительном обследовании рынка Из анализа дерева решений следует, что необходимо проводить дополнительное исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение. Если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно строить большое предприятие (ожидаемая максимальная прибыль 116400 руб.), если прогноз неблагоприятный - малое (ожидаемая максимальная прибыль 12400 руб.).
Поиск по сайту: |
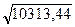 = 101,56.
= 101,56.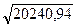 = 142,27.
= 142,27. = 108,21.
= 108,21. = 0,0915 против аналогичного показателя для мягкой зимы, равного
= 0,0915 против аналогичного показателя для мягкой зимы, равного  = 0,1777, т.е. вновь различие почти в 2 раза.
= 0,1777, т.е. вновь различие почти в 2 раза.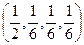 найдите минимальный средний ожидаемый риск.
найдите минимальный средний ожидаемый риск. .
. найдите максимальный средний ожидаемый выигрыш.
найдите максимальный средний ожидаемый выигрыш.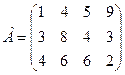 .
. .
.


 лии, когда фирма-монополист может реализовать угрозу подавления потенциальных конкурентов. Причины такой устойчивости могут быть разными. Возможно, сказываются какие-то естественные условия производства, технологические особенности или факторы, позволяющие фирме-монополисту гибко реагировать на действия потенциальных конкурентов (большой запас мощностей, реклама, научный задел, наличие завершенных опытно-конструкторских разработок и т.д.).
лии, когда фирма-монополист может реализовать угрозу подавления потенциальных конкурентов. Причины такой устойчивости могут быть разными. Возможно, сказываются какие-то естественные условия производства, технологические особенности или факторы, позволяющие фирме-монополисту гибко реагировать на действия потенциальных конкурентов (большой запас мощностей, реклама, научный задел, наличие завершенных опытно-конструкторских разработок и т.д.).