 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вероятностная постановка принятия предпочтительных решений
Риск - категория вероятностная, поэтому в процессе оценки неопределенности и количественного определения риска используют вероятностные расчеты. Вероятностные задачи характеризуются тем, что эффективность принимаемых решений зависит не только от детерминированных факторов, но и от вероятностей их появления, т.е. известен закон распределения управляемых факторов X в виде:
где Рi - вероятность появления управляемого фактора хi, i = Каждой паре (хi, Рi) соответствует значение функции эффективности A(хi, Рi). В качестве показателей эффективности используются: - математическое ожидание (М):
-дисперсия (D):
- среднее квадратическое отклонение (σ):
- коэффициент вариации (V):
где Величина М представляет собой обобщенную количественную характеристику и не позволяет принять решение в пользу какого-либо варианта вложения капитала. Важной характеристикой, определяющей меру изменчивости возможного результата, является дисперсия. Чем больше дисперсия, тем в среднем больше отклонение, т.е. выше неопределенность и риск. Поэтому за степень рискованности принимают величину среднего квадратического отклонения. Среднее квадратическое отклонение σ является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости. Дисперсия не дает полной картины линейных уклонений ∆Х = X – М, более наглядных для оценивания рисков. Тем не менее, задание дисперсии позволяет установить связь между линейным и квадратичными отклонениями с помощью неравенства Чебышева. Вероятность Р того, что случайная величина X отклоняется от своего математического ожидания больше, чем на заданный допуск ε > 0, не превосходит ее дисперсии, деленной на ε2, т.е.
Отсюда видно, что незначительному риску по среднеквадратическому отклонению соответствует малый риск и по линейным отклонениям: точки X с большой вероятностью будут располагаться внутри ε - окрестности ожидаемого значения М. Оценка рискованности производится посредством среднего квадратического отклонения σ. Риском операции называется число σ - среднее квадратическое отклонение управляемого фактора (например, дохода) X операции, которое обозначим r = σ. Если под X понимать случайный доход Q, то МQ представляет собой средний ожидаемый доход, или эффективность, а среднее квадратическое отклонение σQ является оценкой рискованности, риском и обозначается rQ. Коэффициент вариации V - безразмерная величина, с его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% - слабая колеблемость, 10-25% - умеренная колеблемость, свыше 25% - высокая колеблемость. С помощью этого метода оценки риска, т.е. на основе расчета дисперсии, стандартного отклонения и коэффициента вариации можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом (проанализировав динамику ее доходов) за некоторый промежуток времени. Преимуществом данного метода оценки риска является несложность математических расчетов, а явным недостатком - необходимость большого числа исходных данных (чем больше массив, тем достовернее оценка риска). Пример 3.1. Сравнить по риску вложения в акции трех типов А, В, С, если каждая из них по своему откликается на возможные рыночные ситуации, достигая с известными вероятностями определенных значений доходности (таблица 3.1). Таблица 3.1 – Вероятности доходностей акций А, В, С для различных ситуаций
Решение. По формулам (3.1 - 3.4) находим для акции А: МА = 20 ∙ 0,5 + 10 ∙ 0,5 = 15%, DA = (20,0 - 15)2 ∙ 0,5 + (10 - 15)2 ∙ 0,5 = 25, σА = для акции В: МВ =15,1 ∙ 0,99 + 5,1 ∙ 0,01 = 15%, DB = (15,1 - 15)2 ∙ 0,99 + (5,1 - 15)2 ∙ 0,01 = 0,99, σВ = для акции С: MС = 13 ∙ 0,7 + 7 ∙ 0,3 = 11,2%, DС = (13 - 11,2)2 ∙ 0,7 + (7 - 11,2)2 ∙ 0,3 = 7,56, σС = Так как наименьшее значение коэффициента вариации имеем для акции В, то и вложения в эту акцию наиболее предпочтительны, тем более, что и σВ = rВ = 0,995% наименьшее. Особый вариант риска – риск разорения. Так называется вероятность столь больших потерь (Х < М), которые ЛПР не может компенсировать и которые, следовательно, ведут к его разорению. Пример 3.2. Пусть случайный доход операции О имеет следующий ряд распределения:
и потери 30 или более ведут к разорению ЛПР. Следовательно, вероятность возникновения риска разорения в результате данной операции равна 0,1 + 0,2 + 0,5 = 0,8. Серьезность риска разорения оценивается именно величиной соответствующей вероятности. Если эта вероятность очень мала, то ею часто пренебрегают (вероятность разорения отлична от нуля почти в любой сделке - из-за весьма маловероятных катастрофических событий на финансовых рынках, в масштабах государства, из-за природных явлений и т.п.). Пример 3.3. Предположим, что на рынке могут возникнуть только два исхода и на каждый из них акции А и В откликаются неслучайным образом. Вероятности этих исходов и соответствующих им значений доходности задаются таблицей 3.2. Таблица 3.2 - Вероятности доходностей акций А и В для различных исходов
Ожидаемые доходности акций: МА = 6 ∙ 0,3 + 2 ∙ 0,7 = 3,2%, МВ = - 1 ∙ 0,2 + 4,25 ∙ 0,8 = 3,2% совпадают, а дисперсии (квадратичные характеристики рисков) равны: DA = (6 - 3,2)2 ∙ 0,3 + (2 - 3,2)2 ∙ 0,7 = 3,36, σА = rА = 1,83, DB = (- 1 - 3,2)2 ∙ 0,2 + (4,25 - 3,2)2 ∙ 0,8 = 4,41, σВ = rВ = 2,1. Предположим теперь, что инвестор взял деньги в долг под процент, равный 2,5%. Ставка процента по кредиту ниже ожидаемой доходности по акциям, которые будут приобретены на заемные деньги, поэтому действия инвестора вполне разумны. Однако, если инвестор вложил деньги в акции А, то при исходе 1 он выиграет (6 - 2,5) = 3,5%, а при исходе 2 проиграет (2 - 2,5) = - 0,5%, причем с вероятностью Р2 = 0,7. Напротив, если он вложит деньги в актив В, то разорение ему грозит с вероятностью Р1 = 0,2 в первой ситуации (исход 1), когда он теряет (- 1 - 2,5) = - 3,5%. Ожидаемые потери (П) при покупке акций А и В составят соответственно: ПА = 0,5 0,7 = 0,35, ПВ = 3,5 ∙ 0,2 = 0,7. Данные потери в первом случае меньше. Однако риски разорения, оцениваемые через вероятность наступления события, наоборот, при приобретении акций А будут больше (0,7 > 0,2). Это превышение возможности банкротства должно отпугивать осторожного вкладчика, который к тому же «играет» на заемном капитале, от акции А в пользу бумаг В. В свою очередь, ожидаемый риск ПА < ПВ склоняет его к выбору в пользу акций А. Каким образом действовать в подобной ситуации инвестору, зависит от его индивидуальных предпочтений, выражаемых в том числе, функцией полезности инвестора.
Поиск по сайту: |
 .
. ; (3.1)
; (3.1) ; (3.2)
; (3.2) ; (3.3)
; (3.3) , (3.4)
, (3.4) - среднее ожидаемое значение квадрата рассматриваемой величины.
- среднее ожидаемое значение квадрата рассматриваемой величины. . (3.5)
. (3.5) = 5, VА =
= 5, VА =  ;
;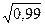 = 0,995, VB =
= 0,995, VB =  ;
; = 2,75, VС =
= 2,75, VС =  .
.