 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
О КЛАССИЧЕСКОЙ ТОНАЛЬНО-МОДУЛЯЦИОННОЙ СИСТЕМЕ
(к проблемам родства тональностей, модуляции и отклонений, темперации) Уже вопрос о трех функциях, а в еще большей степени вопрос о соотношении мажора и минора так или иначе приводил к проблеме родства тональностей. Но с модуляцией и родством тональностей связана еще одна из важных причин выделения среди старинных ладов именно ионийского и эолийского. На этой причине мы и остановимся. В предыдущей главе вскользь упомянуто, что та взаимная симметрия в расположении мажорных и минорных трезвучий, которая свойственна соотношению ионийского и эолийского ладов, присуща и соотношению ладов лидийского и фригийского, а также миксолидийского и дорийского. В этом легко убедиться из схемы, приведенной в примере 42 на стр. 323 и допускающей неограниченное продолжение в обе стороны. Если исключить из нее два трезвучия, выходящие за пределы натуральной диатоники (эти трезвучия поставлены в скобки), то можно сделать исходным моментом последовательности не только до-мажорное и ля-минорное трезвучия, но и любую аналогичную пару противоположных трезвучий, находящихся в схеме на одной вертикали (то есть фа и ми, соль и ре). Поскольку же в приведенной диатонике белых клавиш звуки фа, ми, соль и ре служат тониками лидийского, фригийского, миксолидийского и дорийского ладов, взаимная гармоническая симметрия соответствующих ладов становится очевидной. Она вытекает из простого факта симметрии диатоники белых клавиш относительно звука ре — факта, который надо было бы сообщать уже в курсах музграмоты и элементарной теории музыки. А относительно этого центра (ре) каждая из трех пар трезвучий — на до и на ля, на фа и на ми, на соль и на ре расположена симметрично. Отсюда и следует, что взаимность родства двух тональностей различного ладового наклонения сохранились бы и в том случае, если бы мажор имел лидийскую структуру, а минор — фригийскую (или же мажор — миксолидийскую, а минор — дорийскую). С этой точки зрения пара ладов ионийский-эолийский не имеет преимуществ перед двумя другими парами. Однако взаимность родства требуется не только для тональностей разных ладовых наклонений, но и для двух тональностей одного наклонения. Условиям же такой взаимности удовлетворяют, как будет здесь показано, только ионийский мажор и эолийский минор. Действительно, представим себе чисто теоретически положение, которое возникло бы, если бы классическая система гармонии строилась на основе, например, миксолидийского мажора. Тогда тональность до миксолидийская оказалась бы близкой к тональности ре миксолидийской, ибо все звуки до-мажорного трезвучия входят в миксолидийскую гамму от ре. Но взаимности не было бы, так как не все звуки ре-мажорного трезвучия входят в миксолидийскую гамму от до (не входит фа-диез). Подобным же образом выяснилось бы, что тональность до миксолидийская близка к тональности соль миксолидийской, но не наоборот, ибо в тональность до миксолидийскую не входит соль-мажорное трезвучие (нет звука си, есть си-бемоль). Нетрудно удостовериться, что и при лидийской структуре мажора тоже не будет взаимного родства: тональности ре (лидийская) и соль (лидийская) окажутся близкими для тональности до (лидийской), но не наоборот. То же самое можно повторить по отношению к дорийскому и фригийскому минору. Так, тональности ми дорийская и ля дорийская близки к ре дорийской, ибо минорные трезвучия на звуках ми и ля входят в дорийскую гамму от ре. Однако взаимности нет: в дорийском ля миноре и ми миноре нет звука фа-бекар, входящего в ре-минорное трезвучие, а есть фа-диез. (Точно так же «без взаимности» близки к фригийскому ми минору фригийские ре минор и ля минор: оба последних трезвучия содержатся во фригийской гамме от ми, а ми-минорное трезвучие не содержится во фригийских гаммах от ре и ля). Между тем любая степень родства двух обычных мажорных (ионийских) тональностей, как и двух минорных (эолийских), взаимна. Констатировать этот факт можно посредством простой эмпирической проверки, так как число возможных случаев ограничено. Но такая проверка не выясняет внутреннего смысла факта, его причин и существенных связей. М. Иглицкий в названной работе доказал математическим методом, что определяемое по Римскому-Корсакову родство тональностей обладает свойством взаимности. Однако для уяснения этого доказательства требуется такая математическая подготовка или культура математического мышления, какими не обладает подавляющее большинство читателей музыкантов. И если музыкально-структурное существо вопроса не схватывается при упомянутой простой эмпирической проверке, то оно ускользает и при предельно обобщенном математическом подходе. Зато оно легко обнаруживается при анализе соответствующих музыкально-конструктивных условий и закономерностей. Каким же условиям, обеспечивающим взаимность родства, удовлетворяет структура мажорного лада? Такое условие только одно. Оно необходимо и достаточно: все нетонические мажорные трезвучия мажорного лада симметрично расположены относительно тонического трезвучия. Иначе говоря, любому мажорному трезвучию, отстоящему на какой-либо интервал от тоники (вверх или вниз), соответствует мажорное трезвучие, отстоящее на такой же интервал от тоники, но отсчитываемой в противоположном направлении. И в самом деле: в мажоре есть мажорные трезвучия, отстоящие на кварту в обе стороны от тоники и на квинту в обе стороны; других же нетонических мажорных трезвучий нет. Необходимость такой структуры для взаимности родства вытекает из того очевидного обстоятельства, что если одно из двух трезвучий лежит выше другого на определенный интервал, то это последнее лежит ниже первого на тот же интервал. Действительно, взаимность родства требует, чтобы тоническое трезвучие любой из двух близких между собой тональностей входило в систему другой тональности. Но одно из этих трезвучий лежит настолько же выше второго, насколько второе лежит ниже первого. Следовательно, поскольку речь идет о двух мажорных тональностях, требованию взаимности родства удовлетворяет только такая структура мажорного лада, при которой его мажорные трезвучия расположены на одинаковые интервалы вверх и вниз от тоники. Например, соль-мажорное трезвучие входит в систему до мажора и лежит квинтой выше тоники. А для того чтобы система соль мажора, в свою очередь, содержала до-мажорное трезвучие, надо, чтобы в до мажоре соответственно имелось фа-мажорное трезвучие, то есть — в более общей форме — чтобы в мажорном ладе существовало мажорное трезвучие, лежащее квинтой ниже тоники, коль скоро в нем налицо мажорное трезвучие, расположенное квинтой выше тоники. Ионийский мажор, как сказано, удовлетворяет этому условию. Напротив, лидийский мажор и миксолидийский мажор ему не удовлетворяют. Мажорные трезвучия этих ладов расположены относительно их тоник асимметрично: в лидийском ладу есть мажорные трезвучия, находящиеся секундой и квинтой выше тоники, но нет таких трузвучий, лежащих секундой и квинтой ниже; в миксолидийском, наоборот, мажорные трезвучия имеются на секунду и квинту вниз от тоники, но их нет на те же интервалы вверх. Именно по этой причине родство мажорных тональностей не могло бы быть взаимным, если бы структура мажора соответствовала лидийскому или миксолидийскому ладу. Рассуждения, подробно проведенные здесь для мажора, могут быть повторены и для минора. Необходимым и достаточным условием того, чтобы близость двух минорных тональностей удовлетворяла требованию взаимности, является такая структура минорного лада, при которой все нетонические минорные трезвучия этого лада располагаются симметрично относительно тонического трезвучия. Очевидно, что этому условию отвечает именно эолийский минор, но не фригийский или дорийский. В итоге, принимая во внимание сказанное в предыдущей главе, можно сформулировать два структурных свойства классической системы гармонии, которые в их совокупности обеспечивают взаимность родства тональностей и тем самым — двусторонность модуляционных путей: 1. В мажоре все мажорные трезвучия, а в миноре — все минорные расположены симметрично вокруг тонического трезвучия (это обеспечивает взаимность родства тональностей одного ладового наклонения). 2. В миноре трезвучия разных видов расположены противоположным образом по отношению к их распределению в мажоре, то есть имеет место та взаимная симметрия мажора и минора, которая описана в предыдущей главе (это обеспечивает взаимность родства тональностей разных наклонений). Теперь уже видно, что ко всем многочисленным причинам выделения ионийского и эолийского ладов присоединяется еще одна — и весьма существенная. Классическая функциональная логика как основа формообразования требует своего продолжения за пределами одной тональности в виде отклонений, модуляций, сопоставлений тональностей в самых различных масштабах. Удовлетворить же требованиям модуляционной логики, базирующейся прежде всего на двусторонних связях тональностей, могут только мажор и минор, выросшие на основе ионийского и эолийского ладов. Указанным требованиям удовлетворяют и натуральная диатоника мажора и минора, и расширенная диатоника, включающая в минор мажорную доминанту, а в мажор — минорную субдоминанту. Возникает вопрос, каковы в этом отношении свойства различных других систем мажора и минора, выходящих за пределы диатоники, например десятитоновой мажоро-минорной системы Катуара или системы Яворского. Рассмотрим прежде всего полный мажор и полный минор по Яворскому. Как видно из схем, приведенных в примерах 30 и 41 на стр. 277 и 311, эти лады содержат по девять звуков — три устоя и шесть неустоев. Из двенадцати звуков темперированной системы в лад не входят три звука — те, которые образуют интервал тритона по отношению к звукам тонического трезвучия. Это, как уже упоминалось, имеет, с точки зрения Яворского, очень большое значение. Только отсутствие в ладу тритонов к тоническим звукам и позволяет, по Яворскому, последним быть устойчивыми. Наоборот, наличие тритонов к этим звукам сделало бы их неустойчивыми, тяготеющими, ибо по Яворскому тритон — источник неустойчивости, тяготения, ладового движения. Концепция родства тональностей Яворского предполагает только две возможности: тональности могут быть родственными или неродственными, причем в последнем случае они даже как бы вступают в конфликт. Две тональности считаются родственными, если между звуками их тонических трезвучий нигде не возникает интервал тритона. Если же он есть — тональности не родственны. Например, тональности C-dur и D-dur — не родственны (тритон с — fis), как не родственны C-dur и g-moll (тритон е — b), C-dur и A-dur (тритон g — cis). Наоборот, C-dur и E-dur, C-dur и c-moll, C-dur и gis-moll — родственны. Обратим внимание на то, что такое понимание автоматически обеспечивает взаимность родства: сразу говорится о двух тональностях на равных (симметричных) основаниях, в отличие от общепринятого определения (Римского-Корсакова), которое по своей форме говорит о родстве «в одну сторону» (то есть «тональностями, близкими к данной, считаются... », а не «две тональности близки, если... »). Интересно, однако, что определение Яворского, внешне столь непохожее на обычное, совпадает с ним по его общему смыслу. Действительно, поскольку по Яворскому в систему данной тональности не входят те и только те звуки, которые образуют интервал тритона с каким-либо звуком тонического трезвучия, то все мажорные и минорные трезвучия, не образующие тритонов с тоническим трезвучием данной тональности (то есть все тоники родственных — по Яворскому — тональностей), непременно входят в систему данной тональности и, следовательно, служат представителями родственных тональностей также и в общепринятом смысле. Таким образом, формулировки «две тональности родственны, если их тонические трезвучия не образуют тритонов» и «две тональности родственны, если тоническое трезвучие любой из них содержится в системе другой» оказываются в данном случае (то есть в системе Яворского) эквивалентными. Это не значит, конечно, что круг тональностей, родственных данной по Яворскому, фактически совпадает с кругом тональностей первой степени родства по Римскому-Корсакову, ибо в мажор входит, согласно Яворскому, по девять звуков, а кроме того, Яворский отождествляет энгармонически равные звуки. Поэтому, например Е-dur'ное трезвучие — e-gis-(as)-h включается в систему C-dur по Яворскому, но отнюдь не по Римскому-Корсакову, хотя самый звук as в гармоническом C-dur содержится. Из сказанного можно сделать важный вывод о структуре мажора и минора по Яворскому: как и в обычном натуральном мажоре и натуральном миноре, в «полном мажоре» Яворского все мажорные трезвучия (а в «полном миноре» — все минорные) расположены симметрично относительно тонического трезвучия. Действительно, формулировка родства двух тональностей по Яворскому, говорящая об отсутствии тритона между звуками их тонических трезвучий, с одной стороны, обеспечивает взаимность родства (ибо эта формулировка, как сказано, ставит обе тональности в одинаковое положение), с другой же стороны, эквивалентна формулировке Римского-Корсакова. Последняя, однако, сама по себе не обеспечивает взаимного родства, и необходимым условием взаимности является описанное симметричное расположение трезвучий. Но коль скоро по Яворскому взаимность уже налицо (а она гарантирована соответствующим двусторонним определением: нет тритона между тониками двух тональностей), значит упомянутое структурное условие выполнено. Поэтому до всякой эмпирической проверки можно заранее быть уверенным, что в полном мажоре Яворского все мажорные трезвучия (а в полном миноре — все минорные) расположены симметрично вокруг трезвучия тонического. И в самом деле, кроме тонического, доминантового и субдоминантового трезвучий, в такую систему мажора входят трезвучия, отстоящие от тонического на большую терцию вверх и вниз: например, в C-dur е — gis (as)— h и as — с — es(dis). Аналогичная картина — в миноре. Например, в полном а-moll, кроме трех минорных трезвучий, входящих в диатонику, есть два минорных трезвучия на расстоянии большой терции вверх и вниз от тонического: cis (des) —е—gis и f — as (gis) — с. Что же касается условия взаимности родства двух тональностей разного ладового наклонения, то в концепции Яворского оно выполнено автоматически, ибо минор строится симметрично по отношению к мажору. В итоге любая мажорная или минорная тональность имеет по десять родственных и по тринадцать неродственных тональностей. Среди родственных — четыре тональности того же наклонения и шесть — противоположного. До мажору родственны: c-moll, d-moll, e-moll, E-dur, f-moll, F-dur, G-dur, gis-moll, As-dur, а-moll. Ля минору — A-dur, G-dur, F-dur, f-moll, E-dur, e-moll, d-moll, Des-dur, cis-moll, C-gur. He принимая теорию Яворского в целом, можно, однако, констатировать, что связанная с нею система родства тональностей обладает достаточной внутренней стройностью и замкнутостью, удовлетворяя принципу взаимности. Наоборот, например, десятитоновая мажоро-минорная система, объединяющая натуральные диатоники двух одноименных тональностей, такого рода замкнутостью не обладает. Так, в дополнение к трем мажорным трезвучиям диатоники она включает три мажорных трезвучия на VII, III и VI низких ступенях, которые не располагаются симметрично вокруг тоники. Поэтому «мажоро-минорное родство тональностей» (то есть родство в пределах этой десятитоновой системы) не могло бы удовлетворять требованию взаимности: например, си-бемоль мажорное и ми-бемоль мажорное трезвучия входят в десятитоновую систему до мажоро-минора, но до-мажорное трезвучие не входит в десятитоновые системы си-бемоль и ми-бемоль мажоро-минора. Это и показывает, что мажоро-минорная система не является замкнутой с модуляционной точки зрения. Но почему столь существенна взаимность родства? Не только потому, что в противном случае было бы логически не вполне правомерно применять самый термин родства. Гораздо важнее, чем безупречное употребление терминов и чем формальная красота симметричной и замкнутой тонально-модуляционной системы, практическая сторона вопроса: как уже сказано в предыдущей и в этой главах, взаимность родства тональностей необходима, чтобы обеспечить возможность двусто- роннего движения по всем модуляционным путям (модуляционным планам). Иначе говоря, взаимность родства позволяет осуществить постепенную возвратную модуляцию в некую исходную тональность через те же самые промежуточные звенья (тональности), которые были использованы для первоначальной модуляции из этой тональности. Возможность, о которой идет речь, реализуется в очень многих случаях. Так, она имеет значение для классических сонатных разработок. Некоторые из них содержат своеобразные волны модуляционных уходов и возвратов, часто всего одну такую волну. При этом возврат нередко осуществляется тем же путем, что и уход, и тогда возникает симметрия тонально-модуляционного плана всей разработки. Например, в первой части сонаты Бетховена f-moll, op. 2 № 1 план разработки таков: As — b — с— b — As (и предъикт). В финале сонаты cis-moll, op. 27 № 2 — Cis — fis — G — fis — cis. В первой части сонаты c-moll, op. 10 № 1 — С — f — b — Des — b — f — с. Едва ли этого рода симметричные конструкции заслуживают особых восторгов, которые расточаются некоторыми музыковедами, как только в произведении обнаруживается какая-либо правильность, планомерность и т. д. Ибо такая симметрия представляет собой скорее нечто само собой разумеющееся, подобно тому как при возвращении по улице мы видим те же самые дома, но в обратном порядке. Другими словами, здесь нет какого-либо художественного открытия; проявляется лишь одно из важных технических свойств классической модуляционной системы — возможность двустороннего движения по всем модуляционным путям. Значение этого свойства не следует, конечно, переоценивать, а тем более абсолютизировать: возвратная модуляция может идти по тому же плану, что и прямая, но не обязательно должна. Более того, нередко эстетически удовлетворительное впечатление производит именно новый способ модуляции, в частности быстрый возврат в исходную тональность посредством внезапной модуляции, после того как удаление совершалось медленно и постепенно (или, наоборот, постепенный возврат после быстрого ухода). В повседневной жизни обратное путешествие тоже не всегда предпочтительно осуществить по тому же самому пути. Иногда, например, расписание поездов или другие обстоятельства могут сделать более удобным возвращение по воде (или воздуху). На реке важен вопрос, приходится ли плыть по течению или против, а при ходьбе по неровной местности — ведет ли путь в гору или под гору, насколько крутым является подъем или спуск и т. д. И все же простейшие и давно укоренившиеся представления об обычном передвижении, путешествии связаны с предположением о возможности возвращения той же дорогой. Пусть иногда новая дорога представляется даже более заманчивой и путник ее ищет, но сознание самой возможности вернуться в случае не- обходимости также и прежней дорогой психологически для него очень важно. Теория постепенной модуляции и связанного с ней родства тональностей как раз и относится к такого рода основному, обычному, плавному типу модуляционного движения (как бы пешком и по ровной местности), имеющему большое значение для логики классической музыкальной формы. Вернемся к трактовке тональности и родства тональностей, данной Римским-Корсаковым. Она представляет собой одно из крупнейших достижений теоретического музыкознания. Обобщая некоторые существенные стороны классической модуляционной техники, система родства тональностей Римского-Корсакова служит действенным инструментом в процессе обучения музыкантов, которым надлежит овладеть этими сторонами. Сам Римский-Корсаков считал, что «сродство строев и общие аккорды» составляют «главное основание модуляции», и сетовал на то, что существующие учебники обычно обходят это основание (см. предисловие к Практическому учебнику гармонии). Упрек Римского-Корсакова относился, очевидно, и к превосходному во многих отношениях Руководству Чайковского, где о родстве тональностей упоминается лишь вскользь (в параграфе пятом) и не предлагается никакой системы. Что же касается трактовки родства тональностей у других теоретиков (как у предшествующих Римскому-Корсакову, так и у подавляющего большинства последующих), то она исходила либо из различия в числе ключевых знаков между сравниваемыми тональностями (так поступали не только теоретики середины XIX века, но и, например, Шенберг, Harmonielehre которого появилась в 1911 году), либо из интервальных отношений между их тониками: говорилось о родстве квинтовом, терцовом, а в последние десятилетия — о секундовом (септимовом), даже тритоновом1. В некоторых работах любое интервальное отношение трактуется как некий тип родства и фактически никакой теории или системы родства тональностей не возникает. Известная же схема Римана, предложенная в его работе «Систематическое учение о модуляции как основа учения о музыкальных формах» и сочетающая квинтовый и терцовый принципы, оказалась громоздкой и запутанной. Подход к проблеме у Римского-Корсакова отличался гораздо большей глубиной и широтой, сохраняя при этом достаточную простоту. Римский-Корсаков исходил не из интервалов или ключевых знаков, а из системы данной тональности в целом: мажорные и минорные трезвучия, все звуки которых вхо- 1 Например, Мартин Фогель (Martin Vogel) учитывает возможность рассматривать малую септиму от тоники как 7-й обертон и на этом основании вводит понятие септимового родства (см. упомянутую выше его работу о тристанаккорде). Тритоновое же родство акцентируется, например, в концепции Лендваи, о которой речь будет в главе десятой. дят в систему данной тональности, являются тониками тональностей ближайшего родства по отношению к данной. Дальнейшие же степени родства фактически опираются на первую степень, последовательно выводятся из нее тем способом, какой именуется в математике полной индукцией (подробнее — ниже). При этом весьма существенно, что, определяя самую систему тональности, Римский-Корсаков мудро учитывал и семиступенную диатоническую основу лада и то, что композиторы-классики, во-первых, несравненно чаще применяют в миноре гармоническую (мажорную) доминанту, нежели натуральную (минорную), во-вторых, постоянно осуществляют плавную модуляцию через общий аккорд из мажорной тональности в минорную, лежащую квартой выше (и обратно). Эти реальные факты творческой практики и побуждают признать соответствующие тональности близкими (несмотря на различие в четыре ключевых знака) и ввести мажорную доминанту минора, а следовательно, и минорную субдоминанту мажора, в систему данной тональности1. Может возникнуть вопрос, необходимо ли числить в системе минора также и натуральную доминанту, раз она, как гармония, применяется классиками сравнительно редко. Утвердительный ответ определяется, во-первых, тем, что модуляция в тональность натуральной доминанты совершается, наоборот, очень часто, во-вторых (и это главное) — принципом взаимности родства. Ведь, например, ля-минорное трезвучие входит в систему ми минора в качестве субдоминанты. Следовательно, ми-минорное трезвучие должно входить в систему ля минора, где оно и служит натуральной доминантой. Степень родства двух тональностей имеет следующий общий смысл: она указывает минимальное число модуляционных шагов, которое необходимо (в принципе; в отдельных конкретных случаях, о которых речь впереди, есть еще дополнительные условия) для постепенного перехода из одной тональности 1 Римский-Корсаков писал, что «отношение минорной субдоминанты представляет собой одно из могущественных средств постепенной модуляции в значительно удаленные друг от друга строи» (Учебник гармонии, § 174, цит. изд. ). Ясно, что Римский-Корсаков имел при этом в виду минорную субдоминанту мажора, равно как и мажорную доминанту минора. Для того чтобы не применять всякий раз громоздкие выражения «минорная субдоминанта мажора или мажорная доминанта минора» либо «тональность минорной субдоминанты мажора или мажорной доминанты минора», мы будем иногда говорить для краткости о тональностях или трезвучиях четырехзнакового квинтового отношения (имеется в виду формально разница в четыре ключевых знака, а по существу соотношение, которое акцентирует Римский-Корсаков). Аналогичным образом мажорное и минорное трезвучие (и тональности) могут находиться в двухзнаковом квинтовом отношении (или в миксолидийско-дорийском отношении: одно служит для другого миксолидийской доминантой, а второе для первого — дорийской субдоминантой). Наконец, если в квинтовом отношении находятся два мажорных или два минорных трезвучия (либо две тональности одного наклонения), естественно говорить о простом или однознаковом квинтовом отношении, ибо соответствующие тональности разнятся на один ключевой знак. в другую, то есть для перехода, предполагающего близость (первую степень родства) любых двух соседствующих в этом модуляционном процессе тональностей. Модуляция в тональности первой степени родства, естественно, предполагает всего один такой шаг. Модуляция в тональность второй степени родства требует двух подобных шагов, несмотря на наличие между системами исходной и конечной тональностей общих трезвучий: переход непосредственно через такое общее трезвучие звучит, вообще говоря, недостаточно плавно и законченно, поскольку тоническое трезвучие новой тональности не содержится в системе прежней. Этого рода модуляция встречается, конечно, в творческой практике и допускается учебником Римского-Корсакова, однако называется несовершенной, в отличие от совершенной, предполагающей, что затрагивается не только общий аккорд, но и соответствующий промежуточный строй (тональность). Для совершенной (постепенной) модуляции в тональность третьей степени родства требуются две промежуточные тональности и, следовательно, три модуляционных шага. В этом указании количества необходимых шагов при постепенной модуляции из одной тональности в другую и состоит практический смысл распределения всех соотношений тональностей по степеням родства. Определения и конкретные примеры, содержащиеся в Практическом учебнике Римского-Корсакова, требуют, однако, ряда уточнений и разъяснений. Что касается определения первой степени родства, которое уже приведено в предыдущей главе, то, поскольку существует взаимность родства, обеспеченная, как мы видели, самой структурой мажора и минора, оно безупречно. Правда, наряду с ним может существовать равносильное ему двустороннее, симметричное определение (две различные тональности находятся в первой степени родства, если тоническое трезвучие любой из них входит в систему другой), но определение Римского-Корсакова сохраняет свой практический смысл, так как фактически модуляция происходит из некоей данной тональности в другую, а кроме того, в произведении имеется главная тональность; поэтому важно указать круг тональностей, близких именно к данной (то есть, иными словами, целесообразность логически «одностороннего» определения в данном случае несомненна). Вторая степень родства определяется в § 58 Практического учебника следующим образом: «Под строями 2-й степени сродства к данному строю мы разумеем строи, которых тонические трезвучия не заключаются в, данном строе, но тем не менее имеющие с ним по крайней мере одно общее трезвучие». После этого Римский-Корсаков указывает, что всякий мажорный или минорный строй имеет по 12 строев, находящихся с ним во вто- рой степени родства, и перечисляет эти строи по отношению к до мажору и ля минору. Обратим внимание на то, что приведенное определение уже приближается к двустороннему, ставящему две сравниваемые тональности в равное положение (тональности «имеющие... общее трезвучие»). Более существенно, однако, что это определение применяет в скрытом виде так называемую математическую индукцию, то есть определяет вторую степень родства через первую, хотя и не содержит явного упоминания о ней. Действительно, если две тональности имеют общее трезвучие, то каждая из них находится в первой степени родства с той тональностью, где это трезвучие служит тоникой. Точно так же часть определения: «строи, которых тонические трезвучия не заключаются в данном строе» — равносильна формуле: «строи, которые не находятся с данным в первой степени родства». Поэтому определение Римского-Корсакова можно заменить (по Иглицкому) определением, внешне более громоздким, но зато обнажающим логическую сущность всей системы степеней родства: тональностью второй степени родства по отношению к данной называется всякая тональность, которая отлична от данной и не находится с ней в первой степени родства, но находится в первой степени родства, по меньшей мере, с одной тональностью, состоящей в первой степени родства с данной тональностью. Двустороннее определение было бы менее громоздким: две различные тональности находятся во второй степени родства, если они не состоят в первой степени родства, но существует тональность, находящаяся в первой степени родства с каждой из них. Аналогичным образом, предполагая, что вторая степень родства уже определена, можно дать следующие определения третьей степени. Первое (одностороннее, исходящее из данной тональности): тональностью третьей степени родства по отношению к данной называется всякая отличная от нее тональность, которая не находится с ней ни в первой, ни во второй степени родства, но находится в первой степени родства, по меньшей мере, с одной тональностью, состоящей во второй степени родства с данной тональностью. И второе (двустороннее): две различные тональности находятся в третьей степени родства, если они не состоят между собой в более близком родстве и если существует тональность, находящаяся в первой степени родства с одной из этих тональностей, и во второй степени родства — с другой. Речь, конечно, вовсе не идет о том, чтобы заменить более сложными определениями простые определения, содержащиеся в Практическом учебнике гармонии Римского-Корсакова. Громоздкие формулировки приведены здесь только для того, чтобы раскрыть единую внутреннюю логику всей системы родства, а также ее практический смысл, связанный с указанием мини- мального числа модуляционных шагов, необходимых (в принципе) при постепенной модуляции из одной тональности в другую. Без этого не были бы ясны некоторые из дальнейших, развиваемых здесь соображений1. В формулировках, касающихся модуляции, есть в Практическом учебнике гармонии также некоторая недоговоренность, а кое в чем и очевидная непоследовательность. Так, в § 48 сказано, что за вычетом тональностей первой степени родства «все прочие строи... будут далекими или строями 2-й, 3-й и т. д. степеней». А в § 61, носящем заглавие «Далекие или отдаленные строи», первая фраза гласит: «За исключением строев 1-й и 2-й степени сродства к данному строю, все прочие строи... считаются отдаленными». Таким образом, поскольку в заглавии § 61 слова «далекие» и «отдаленные» трактуются как синонимы, оказывается, что тональности второй степени родства в одном случае названы далекими (§ 48), а в другом, наоборот, исключены из далеких (§ 61). Вероятно, эта непоследовательность возникла из-за того, что в ранее написанном Римским-Корсаковым Учебнике гармонии не было понятия степеней родства и все строи делились на «близкие» и «дальние» (§ 140 Учебника). В Практическом же учебнике гармонии, с одной стороны, сохранилась более или менее сходная формулировка (§ 48), с другой же стороны, тональности второй степени родства, как имеющие общие трезвучия с данной тональностью, были выделены в самостоятельную группу и исключены из собственно далеких (дальних, отдаленных). В итоге слово «далекие» применено в Практическом учебнике с двумя различными оттенками: в первом случае (§ 48) оно означает лишь «не близкие», во втором (§ 61) — далекие в более тесном смысле (отдаленные, дальние), то есть предполагающие не только «не близость», но и достаточно большую степень удаленности. В приведенной формулировке из § 48 есть также следующий не вполне ясный и не раскрытый в учебнике момент: говорится о строях «2-й, 3-й и т. д. степеней». Это «и т. д. » как будто предполагает наличие по крайней мере четвертой степени, между тем как в § 61 ничего не говорится даже о третьей степени, а все строи, кроме строев первой и второй степени родства, названы отдаленными. Таким образом, оставлен открытым вопрос, сколько же существует степеней родства и, вообще, ограничено ли их число2. 1 Внутренняя логика системы родства тональностей Римского-Корсакова фактически основана, как мы показали, на принципе полной математической индукции: определяется первая степень и указывается, как определить любую последующую (n+1), если определена предыдущая (n) 2 В экземпляре литографированного издания Учебника гармонии, принадлежавшем Римскому-Корсакову, рукой автора сделаны карандашные пометки на полях, указывающие соответствующие степени родства в напечатанной таблице модуляционных планов из C-dur и a-moll во все употребительные В сущности в Практическом учебнике гармонии Римского-Корсакова в этом вопросе проявляется некоторая двойственность. С одной стороны, обобщенное понятие «отдаленных строев» как бы объединяет все их в единую «третью степень», внутри которой дифференциация практически уже не существенна. С другой же стороны, упомянутое «и т. д. », а также некоторые приводимые Римским-Корсаковым примеры модуляционных планов (примеры, о которых пойдет речь, введены, начиная с третьего издания учебника) свидетельствуют о том, что в принципе Римский-Корсаков все же допускал дальнейшую дифференциацию отдаленных строев. Действительно, планы эти содержат по четыре модуляционных шага и, следовательно (поскольку четыре шага в данных условиях минимально необходимы), предполагают четвертую степень родства: например, Си—ми—До—ре—Си-бемоль или Ля-бемоль—фа—До—ля—Ми. Однако достаточно энгармонически заменить начальную или конечную тональность, чтобы четвертая степень родства обернулась второй: Ces—es—В; Gis—cis—Е (или As—des—Fes). Таким образом, двойственность позиции Римского-Корсакова отражает двойственность самого предмета, то есть возможность считать или не считать энгармонически равные тональности тождественными. В первом случае окажется, что существуют только три степени родства, ибо каждая из пяти тональностей, не состоящая с данной ни в первой, ни во второй степени родства (а к этим степеням родства относятся 18 тональностей: 6+12), находится, как легко убедиться, в первой степени родства с какой-нибудь тональностью второй степени и, следовательно, принадлежит к третьей степени. В другом случае квинтовый круг тональностей трактуется как спираль с неопределенным или неограниченным числом витков и количество возможных степеней родства приходится тоже признать в принципе неопределенным или неограниченным. Так, для тональности C-dur тональность Eis-dur будет относиться к пятой степени тональности. В этих пометках фигурирует также и четвертая степень родства, например при плане С—d—А—fis—Cis (цит. изд., стр. 134—136). Напомним, что в литографированном тексте учебника о степенях родства речи нет. Карандашные пометки на полях воспроизведены в цитируемом издании редактором тома Вл. Протопоповым. В пометках этих есть некоторые непоследовательности. Так, модуляции на интервал тритона из минора в минор (из a-moll в dis-moll и в es-moll) помечены IV степенью, тогда как наряду с вариантами из четырех шагов (а—G—h—Fis—dis и а—С—f—Des—es) указаны и варианты из трех шагов (а—Е—gis—dis и а—d—В—es). Для аналогичных же модуляций на тритон из мажорной тональности в мажорную (С—Fis и С—Ges) приведены планы, содержащие только три шага, и степень родства помечена карандашом как третья. Между тем из системы Римского-Корсакова вытекает полная симметрия модуляционных планов из мажора и из минора (подробнее об этом ниже). Однако, несмотря на указанные непоследовательности, из этих карандашных пометок все же видно стремление Римского-Корсакова связывать степень родства с числом модуляционных шагов, необходимых для перехода из одной тональности в другую. родства (С—е—Н—dis—ais—Eis), a Fisis — к седьмой (С—е—Н—dis—Ais—cisis—His—Fisis). Тональность, энгармонически равная исходной C-dur (His или Deses), окажется к ней в шестой степени родства (например, С—f—Des—ges—Fes— —heses—Deses). Если же пройти еще один виток спирали, получится, соответственно, двенадцатая степень родства и т. д. В конечном счете вопрос сводится к тому, принимать ли в данном случае темперированный строй или нет. О проблеме темперации в целом речь будет в конце этой главы. Сейчас заметим лишь, что если интонирование голосом и на инструментах с нефиксированной высотой тона и не обязано, конечно, строго придерживаться какого-либо определенного строя (чистого, темперированного или пифагорова), то классическая модуляционная система в принципе не может не исходить из темперации, ибо последняя, собственно, и была введена главным образом ради первой, то есть ради одинакова хорошего звучания всех тональностей, обеспечивающего возможность модуляций в любую из них. Классическая система гармонии, допускающая известную свободу интонирования, в то же время органически связана с равномерно темперированным строем, который предполагает замкнутый квинтовый круг тональностей (а не квинтовую спираль) и наличие 24-х (и только 24-х) мажорных и минорных тональностей при полном их равноправии. Считать же энгармонически равные тональности разными — значило бы нарушить все эти условия: круг превратился бы в спираль, количество тональностей превысило бы 24, и они оказались бы неравноправными. Например, для тональности gis-moll имелась бы мажорная тональность, отстоящая на 11 знаков в сторону бемолей, — это была бы тональность пятой степени родства Ges-dur (gis—Е—а—F—b—Ges), а для тональности es-moll такой тональности не было бы, так как тональность Eseses с 17 знаками в ключе (то есть с четырьмя дубль-бемолями и тремя «трипль-бемолями»: 4×2+3×3=17) реально не существует. Вот почему о степенях родства дальше третьей можно говорить лишь в плане чисто условном1. Другой вопрос, что степень родства указывает лишь минимально необходимое (в принципе) число шагов при постепенной модуляции. Всегда допустимо, а практически иногда и весьма желательно, большее их количество. Так, Римский-Корсаков советует в качестве исключения из общего правила вставлять в постепенную модуляцию добавочное звено, чтобы 1 В противном случае (то есть при отказе от энгармонических замен) пришлось бы признать, что многие классические произведения заканчиваются не в исходной тональности, а в энгармонически равной ей. Так, реприза первой части «Аппассионаты» вступала бы (поскольку в разработке есть две энгармонические замены бемольных тональностей на диезные — в начале и в конце) не в f-moll и даже не в geses-moll, а в asasasas-moll, то есть в тональности двенадцатой степени родства по отношению к исходной. избежать двух кварто-квинтовых модуляционных шагов подряд или слишком близкого сопоставления тоник одноименных тональностей (например, вместо С—F—b или С—f—b предпочтительнее С—f—Des—b или С—а—F—b; вместо С—f—с лучше С—f—Es—с; см. § 58 Практического учебника гармонии). Аналогичным образом большее число шагов может вызываться каким-либо дополнительным требованием к модуляционному плану. Очевидно, в частности, что, поскольку все тональности располагаются по квинтовому кругу, каждая из них может быть достигнута движением от любой другой в двух противоположных направлениях. И добавочное условие иногда заключается как раз в указании определенного направления модуляции (например, только в сторону бемолей), что может заставить двигаться не кратчайшим путем и пройти больше половины «квинтовой окружности». С этой точки зрения уже упомянутые планы Н—е—С—d—В и As—f—С—а—Е, приведенные Римским-Корсаковым, следует понимать не как предполагающие различие между тональностями Н и Ces или Е и Fes, а как подчиненные дополнительному условию: требованию двигаться только в сторону бемолей в первом случае и только в сторону диезов во втором, тогда как кратчайший путь ведет оба раза в обратном направлении (как уже упомянуто Ces—es—В и As—des—Fes). Заметим попутно, что, хотя один модуляционный шаг может иногда давать «выигрыш» сразу в четыре ключевых знака, движение к цели по большей дуге квинтовой окружности никогда не может содержать меньшее число шагов, чем движение по меньшей дуге. Однако для постепенной модуляции в тональность третьей степени родства необходимо одинаковое число шагов (3) при общем направлении модуляции в любую сторону (как по меньшей дуге квинтовой окружности, так и по большей), то есть как без замены какой-либо тональности энгармонически равной, так и с заменой. Преимущество движения по меньшей дуге состоит лишь в большем количестве возможных модуляционных путей, в большем разнообразии вариантов модуляционных планов. Например, при модуляции из C-dur в fis-moll по меньшей дуге (разница в три ключевых знака) в принципе возможны шесть вариантов: четыре прямых (с движением каждого шага только в сторону диезов: С—G—h—fis, С—G—D—fis, С—e—h—fis, С—e—D—fis) и два «с выигрышем в четыре диеза», но без постоянного движения к диезам (С—а—Е—fis и С—d—А—fis). При модуляции же по большей дуге, в сторону бемолей (разница в девять знаков), возможен всего один вариант: С—f—Des(Cis)—fis. Подобный же единственный вариант движения в сторону бемолей возможен и при модуляциях С—cis и С—gis: С—f—As(Gis)—cis и С—f—Es—as(gis). Что касается тональностей, которые требовали бы для перехода из одной в другую по большей дуге квинтовой окружности четырех шагов (иначе говоря, относились бы к четвертой сте- пени родства, не будь энгармонических замен), то они всегда являются тональностями второй степени родства, то есть требуют двух шагов. Точно также любая тональность первой степени родства может быть достигнута пятью шагами в противоположном направлении. Поскольку же обход всего круга требует, как мы видели, шести шагов, логично принять, что данная тональность находится сама с собой как бы в нулевой степени родства1. Из всего сказанного видна большая стройность системы родства тональностей, основанной на принципе Римского-Корсакова. Венчает систему полная симметрия всех модуляционных планов из минорной тональности по отношению к модуляционным планам из мажорной тональности. Симметрия эта, о которой Римский-Корсаков не упоминает, вытекает из противоположного (взаимосимметричного) расположения трезвучий в мажоре и миноре, демонстрируемого Римским-Корсаковым в одной из схем (см. пример 43 на стр. 335 этой книги), но не формулируемого. Из такого расположения непосредственно следует взаимосимметричное распределение и расположение тональностей первой степени родства (для мажора — две мажорные и четыре минорные, для минора — наоборот), а значит и следующих степеней. В итоге каждому модуляционному плану из мажорной тональности соответствует симметрично построенный по отношению к нему план из минорной тональности (речь идет, конечно, о симметрии только в последовательности тональностей, а отнюдь не аккордов). Так, если из мажора в мажор, лежащий полутоном ниже, ведет всего один кратчайший модуляционный план (например, С—е—Н), то из минора в минор, лежащий полутоном выше, тоже ведет один кратчайший план, симметричный по отношению к предыдущему (например, а—F—b). Аналогичным образом, например, плану С—d—А симметрично отвечает план а—G—с, плану С—G—h—Fis — план а—d—В—es и т. д. По интервальной структуре тут налицо инверсия (обращение), но, кроме того, в симметрично отвечающем плане все тональности заменяются тональностями другого лада. Мы показали сейчас, что модуляционным планам из мажора в мажор симметрично отвечают планы из минора в минор. Что же касается планов, ведущих в тональность противоположного наклонения, то, на первый взгляд, симметричное соответствие 1 Следует, однако, заметить, что положения, обратные только что приведенным, не верны не всякая тональность, достижение которой требовало бы пяти шагов при движении по большей дуге квинтовой окружности, является тональностью первой степени родства, и не всякая тональность второй степени родства может быть достигнута четырьмя шагами в противоположном направлении. Например, модуляция из Des-dur в gis-moll требует при движении по большей дуге (то есть без энгармонических замен) пяти шагов (Des—f—С—е—Н—gis). Но Des-dur (Cis-dur) и gis-moll находятся во второй степени родства, а не в первой. Подробнее о такого рода исключениях речь впереди. обеспечивается здесь взаимностью родства и двусторонностью модуляционных путей: те пути, какие ведут из «х-мажора» в «у-минор», ведут и обратно — из «у-минора» в «х-мажор». Однако это соответствие говорит о соотношении типа ракохода, а не обращения (инверсии). Между тем последнее соотношение тоже имеет место, и именно о нем сейчас идет речь. Рассмотрим, например, кратчайшие планы из C-dur в gis-moll. Их всего три: С—а—Е—gis, С—е—Н—gis, С—f—Es—as (gis). Если первый из них мы прочтем от конца к началу (gis—Е—а—С), то убедимся, что возвратное движение отнюдь не образует точной интервальной инверсии. Но это возвратное движение дает точную инверсию второго из приведенных нами планов. И наоборот: возвратное движение по второму плану (gis—Н—Е—С) есть инверсия первого. Третий же план сам внутренне симметричен, поэтому возвратное движение по нему («ракоход») совпадает с его интервальной инверсией. Словом, в отношении модуляционных планов минор есть точное интервальное обращение мажора. Все без исключения планы постепенных модуляций из мажора и из минора находятся в полном симметричном соответствии между собой: для любого плана существует симметричный, заменяющий все участвующие в нем тональности тональностями противоположного лада и все интервалы между тониками этих тональностей такими же интервалами в противоположном направлении1. Критика теории родства тональностей Римского-Корсакова и коррективы к ней, данные в работах последующих авторов, имеют как положительную, так и отрицательную сторону. Положительным является более дифференцированное дальнейшее изучение вопроса, равно как и выяснение всевозможных других связей и соотношений тональностей, роли модуляции в музыкальных формах и т. д. Отрицательным же представляется то, 1 В предыдущей главе уже сказано, что о симметрии модуляционных путей из мажора и из минора кратко упомянуто в работах Ю. Тюлина и А. Должанского. В Практическом курсе гармонии И. Способина, С. Евсеева, И. Дубовского, стр. 134, приведена уже упомянутая в предыдущей главе симметричная схема, распределяющая все тональности по степеням родства (для мажора и для минора). В примечании к схеме говорится: «Обращаем внимание на любопытную симметрию мажорной и минорной половины этой схемы как в отношении числа тональностей каждой категории функционального родства, так и в отношении лада и местоположения их от исходной, первоначальной тональности». Здесь, однако, нет речи ни о том, что симметрия схемы вытекает из взаимной симметрии структуры мажора и минора, ни о том, что из схемы следует симметрия самих модуляционных планов. Между тем знание этого практически очень облегчает отыскание модуляционных путей. Детальный анализ симметрии модуляционных планов из мажора и минора (и само указание на эту симметрию) сделаны в неоднократно упоминавшейся нами работе М. Иглицкого. Ее практическая задача — создание метода безошибочного (автоматического) отыскания всех возможных модуляционных планов (постепенных), ведущих из данной тональности в любую другую. Завершает работу предложенный М. Иглицким графический способ отыскания таких планов. что иногда при этом, наряду с развитием концепции Римского-Корсакова, происходит некоторое искажение самого принципа, лежащего в ее основе, либо же фактическая подмена того вполне определенного и специального понятия родства тональностей, которое имел в виду Римский-Корсаков, гораздо более широким и менее определенным понятием тональных связей. Упрощенный вариант системы родства тональностей Римского-Корсакова содержится в работе Л. Рудольфа1. Близкими Рудольф считает те же тональности, что и Римский-Корсаков. Существенна констатация Рудольфа, что «отношение это может быть только взаимным» (стр. 109), хотя ни причин взаимности, ни вытекающих из нее следствий Рудольф не касается. Различных степеней родства он также не вводит (как и Римский-Корсаков в первом своем труде по гармонии), но дает разнообразные указания для построения всевозможных модуляционных планов, содержащих до пяти шагов включительно (предлагаются примеры модуляций в тональности, отстоящие на 3, 4, 5, 6, 7, 8, 9 знаков). Представляется, конечно, предпочтительным сохранить основанное на темперированном строе деление на три степени родства как имеющее принципиальное значение и облегчающее практическое нахождение модуляционных планов. Дальнейшее развитие теории родства тональностей, исходящее из системы Римского-Корсакова, дано в трудах Ю. Н. Тюлина, о чем речь впереди. Наконец, в этом же направлении идет названная работа М. Иглицкого, в которой исследование ряда вопросов проведено с исчерпывающей полнотой и точностью. Сейчас рассмотрим некоторые системы родства тональностей, существенно отступающие от основ, заложенных Римским-Корсаковым. Одна из них содержится в широко распространенных учебниках гармонии, созданных коллективом московских теоретиков (И. Дубовский, С. Евсеев, И. Способин, В. Соколов). Эта система сохраняет группу тональностей первой степени родства такой, какой она дана Римским-Корсаковым. Группа же тональностей второй степени родства (по Римскому-Корсакову) разделена на две: а) тональности, которые отстоят от данной на два ключевых знака и имеют с ней по два общих трезвучия, лежащих в натуральных системах обеих тональностей, б) остальные тональности, отнесенные Римским-Корсаковым ко второй степени родства и имеющие с исходной тональностью общее трезвучие, лежащее в натуральной системе одной тональности и гармонической системе другой. Эти две группы образуют вторую и третью степени родства, а к четвертой отнесены соответственно те пять отдаленных тональностей (с возможными энгармоническими заменами), которые не имеют общих трезвучий с данной и согласно принципу математической индукции 1 Л. Рудольф. Гармония (Практический курс). Баку, 1939. находятся с ней в третьей степени родства, требуя, следовательно, при постепенной модуляции минимум трех шагов. Причина этой реформы заключается, видимо, в «слишком большом» количестве тональностей второй степени родства по Римскому-Корсакову (напомним, что их двенадцать при шести тональностях первой степени родства и пяти — третьей) и, естественно, в их во многом различных соотношениях и связях с данной тональностью1. Однако эти обстоятельства могли бы оправдать лишь ту или иную дополнительную дифференциацию, то есть детализацию внутри данной группы, не нарушающую логического и практического смысла системы в целом. Например, было бы допустимо разбить всю группу тональностей второй степени родства на две подгруппы А и В, быть может, дав им какие-либо наименования. Но классификация, произвольно увеличивающая само количество степеней родства, представляется очень уязвимой как с логической, так и с практической точки зрения. Действительно, среди тональностей первой степени родства тоже есть сравнительно более близкие и менее близкие. Так, параллельные тональности имеют шесть общих консонирующих трезвучий, их тонические трезвучия — два общих звука, а натуральные диатоники полностью совпадают. Мажорная же тональность и параллель ее субдоминанты (то есть тональность II ступени) имеют лишь четыре общих трезвучия, и у тонических трезвучий этих тональностей вовсе нет общих звуков. Наконец, у тональностей четырехзнакового квинтового отношения есть всего два общих трезвучия, да к тому же каждое из них лежит в натуральной системе лишь одной тональности (и в гармонической — другой). Но сила найденного Римским-Корсаковым обобщения, отражающего важную сторону классической модуляционной техники, в том и состоит, что несмотря на эти раз- 1 В брошюре А. Ф. Мутли «О модуляции» указано, что «говорить о всей группе тональностей 2-й степени родства, как об определенной системе, невозможно» (А. Ф. Мутли. О модуляции Музгиз, М. — Л., 1948, стр. 14). Это указание, видимо, основано на недоразумении: «определенную систему» представляет собой концепция родства тональностей в целом, группа же тональностей второй или третьей степени родства не может претендовать на то, чтобы быть неким органическим единством: ее объединяет только то свойство по отношению к данной тональности, которое заключается именно в соответствующей степени родства, то есть в минимальном количестве плавных модуляционных шагов, необходимом для достижения любой тональности этой группы. Вспомним для сравнения, что если считать находящимися в первой степени родства родителей и детей, супругов, братьев и сестер (то есть лиц, могущих образовать одну семью в тесном смысле), а во второй — лиц, не состоящих в первой степени родства, но имеющих общего родственника первой степени, то вся совокупность родственников второй степени по отношению к данному лицу тоже не образует «определенной системы»: к числу этих родственников относятся, например, и дед и внук данного лица, и его дядя, и его племянник, и его тесть, зять, шурин, и его пасынок либо отчим. личия (имеющие свое значение для дальнейшего дифференцирующего анализа внутри данной группы) все названные тональности относятся к первой степени родства. И нелогично, с одной стороны, признавать корсаковское понимание группы тональностей первой степени родства, куда безоговорочно включаются строи четырехзнакового квинтового отношения, а с другой стороны, отказываться включать в группу второй степени родства те тональности, модуляция в которые идет через эти строи (в качестве промежуточных). Подобный отказ, в сущности, задним числом дискриминирует тональности четырех знакового квинтового отношения как строи именно первой степени родства, дезавуирует, берет назад признание их таковыми. Отсюда вытекает и то, что различие между степенями родства теряет связь с различием в числе минимально необходимых для соответствующей модуляции шагов. Например, переход в тональность как второй, так и третьей степени родства требует двух шагов. Кратчайшая же постепенная модуляция в тональность четвертой степени родства состоит из трех шагов и, следовательно, минует (пропускает) тональность либо второй, либо третьей степени родства: так, в модуляции
Не получается ли, что 1+1=3? И наконец, не ясно ли, таким образом, что предложенная в учебниках группы московских теоретиков, казалось бы, небольшая и невинная реформа системы Римского-Корсакова на деле представляет собой отказ от ее основного логического принципа и связанного с ним практического смысла? Недостаточно продуманная система привела авторов и к одному фактическому несоответствию, оставшемуся незамеченным и переходившему из одного издания учебника в другое. Одноименная тональность, как отличающаяся от исходной более чем на два знака и требующая для модуляции использования четырехзнакового квинтового отношения, причисляется авторами не ко второй, а к третьей степени родства. В то же время всякая тональность третьей степени родства, как утверждали авторы еще в 1935 году, имеет «единственный общий аккорд» с данной1. Это положение повторено и в 1956 году. «Группа тональностей третьей степени родства объединяет для данного мажора и минора по восемь тональностей, имеющих какое-либо одно общее трезвучие лишь в гармоническом ладе» (для C-dur — Es, As, Des, A, E, H, b, с)2. Между тем одноименные тональности имеют не одно, а два общих консонирующих трезвучия (мажорная доминанта и минорная субдоминанта), что не оговорено авторами. Остается добавить, что, хотя группа тональностей второй степени родству по Римскому-Корсакову и допускает ту или иную внутреннюю дифференциацию, сами критерии, на основании которых авторы цитированных сейчас учебников разбили эту группу на две, тоже очень условны. Трудно, например, убедительно обосновать положение, что к до мажору ближе си минор, чем ля-бемоль мажор. Ибо сколь скоро четырехзнаковое квинтовое отношение включено в первую степень родства, разница в количестве знаков перестает быть надежным и основным критерием определения родства, приобретая лишь дополнительное значение наряду с другими факторами (например, наряду с общеизвестной связью одноименных тональностей, которая делает ля-бемоль мажор более близким до мажору, чем си минор). Количество общих трезвучий тоже может служить только добавочным критерием, ибо оно указывает лишь на число путей, по которым может идти постепенная модуляция, но не на их длину (число шагов), определяющую «расстояние» между тональностями, а следовательно, их сравнительную близость или дальность3. Перед тем как перейти к другим теориям родства тональностей, необходимо высказать некоторые более общие соображения. Всевозможные соотношения и связи тональностей очень богаты и многообразны. Некоторые из них используются чаще, некоторые реже. В одних стилях или композиционных условиях 1 См. Практический курс гармонии, ч. II. М., Музгиз, 1935, стр. 133. 2 И. И. Дубовский, С. В. Евсеев, И. В. Способин и В. В. Соколов. Учебник гармонии. Издание четвертое. М., Музгиз, стр. 351. 3 Автор считает своим долгом подчеркнуть, что критику системы родства тональностей, предложенной в учебниках группы московских теоретиков, он отнюдь не распространяет на эти учебники в целом: они заслуживают, по мнению автора, весьма высокой оценки. (частях музыкальной формы) преобладают модуляции в одни тональности, в других — в иные. Есть гармонические связи тональностей, есть и мелодические. Тональность, сравнительно более близкая к данной в каком-либо определенном смысле, может оказаться более далекой в другом смысле, с иной точки зрения. В сущности, любое соотношение тональностей содержит нечто индивидуальное, качественно своеобразное, обладает такой совокупностью свойств и возможностей, какой нет у другого соотношения. Изучать и систематизировать тональные соотношения следует, разумеется, в самых различных планах и аспектах, например с точки зрения их роли в музыкальном формообразовании, в исторической эволюции музыкальных стилей, в постепенном расширении тональных связей и т. д. Но невозможно создать единую систему, которая учитывала бы все мыслимые аспекты и в то же время вполне убедительно разбила бы совокупность многих качественно своеобразных отношений тональностей на несколько групп, расположенных в один ряд по одному порядково-количественному признаку (по «степени близости»). Ибо такое распределение неизбежно требует выделения некоторого основного, решающего критерия, с помощью которого устанавливаются порядковые соотношения и измеряются соответствующие количества (расстояния). Если же такого единого критерия нет, то любая система родства тональностей оказывается весьма условной, и, пожалуй, тем более условной, чем она более детализирована. Наконец, теоретическая система создается с какой-то целью, призвана решать те или иные задачи, отвечать на определенные вопросы. Система родства тональностей Римского-Корсакова отличается ясной целенаправленностью. В пределах максимально широко понимаемой классической гармонии и независимо от более частных стилевых норм, равно как и от того, в каком разделе музыкальной формы и с какой художественной целью делается постепенная модуляция, система эта обобщает (преимущественно в методическом отношении) важную сторону техники таких модуляций, связанную с построением модуляционного плана. Она направлена на отыскание соответствующих планов и представляет собой в определенном смысле теорию близости и удаленности тональностей, то есть их «расстояний», а также учение о преодолении этих расстояний по кратчайшим и наиболее выгодным путям. Ни на какие другие вопросы она не отвечает. И если четко договориться о том, что такое постепенная модуляция и что такое система данной тональности, а значит и первая степень родства, то все остальные степени вытекают автоматически по принципу полной индукции. Некоторые же концепции родства тональностей фактически пытаются ответить и на другие вопросы (о частоте применения тех или иных модуляций в музыкальных формах и в определенных стилях, об исторической эволюции тональных связей) и в результате теряют целенаправленность, не отвечают удовлетворительно ни на один вопрос либо же подменяют один вопрос другим. В повседневной жизни всем ясно, что вопрос: «близко ли от Вас живет этот человек и как я мог бы поскорее добраться до него пешком?» — отнюдь не равнозначен вопросам: «давно ли Вы с ним знакомы?» и «часто ли Вы у него бываете, когда именно и по каким поводам?». В системах же родства тональностей различные вопросы иногда почему-то смешиваются. Напомним еще раз, что система Римского-Корсакова призвана отвечать только на вопросы, аналогичные первому из приведенных: она учит (подчеркнем снова ее методическую направленность) по каким «улицам» и «переулкам» легче всего пройти пешком из одного пункта в другой, причем четырехзнаковые квинтовые соотношения, весьма сокращающие расстояния, как бы уподобляются «проходным дворам» (их открытие — одно из главных достижений концепции Римского-Корсакова). Уже упомянуто, что общее понятие соотношений и связей тональностей шире специального понятия их родства. Особенность ряда систем родства заключается в том, что это специальное понятие как бы растворяется в более общем понятии соотношений и связей тональностей, становится расплывчатым или же приобретает совсем другой смысл. Чтобы убедиться в этом, достаточно познакомиться, например, с ценной по материалу статьей Р. С. Таубе «О системах тонального родства»1. Таубе дает обзор различных систем и предлагает собственную, в которой три основные группы делятся на многочисленные подгруппы, а некоторые тональности рассматриваются как промежуточные, лежащие между группами. В этой статье приведена, в частности, система шести групп родства, принадлежащая И. В. Способину (она излагалась в его лекциях). Вот эта система: «1-я группа — диатонического родства (5 тональностей); 2-я группа — полудиатонического родства (тональность минорной S мажора, тональность мажорной D минора); 3-я группа — мажоро-минора одноименного родства (одноименная Т и ее система, т. е. III низкая, минорная D, VI низкая, VII низкая — в мажоре; II минорная, III высокая, мажорная S, VI высокая в миноре). 4-я группа — мажоро-минора параллельного родства (мажорная III в мажоре, минорная VI в миноре — «шубертова» VI); 5-я группа — тональности неаполитанской гармонии; 6-я группа — отдаленная хроматическая»2. Схема эта отчасти отражает некоторые черты исторического развития тональности и тональных связей, отчасти же — частоту 1 См. «Научно-методические записки Саратовской консерватории», вып. 3. Издательство Саратовского университета, 1959. 2 Там же, стр. 163—164. модуляций в разные тональности. Но она очень непоследовательна и условна. Например, неаполитанская гармония и тональность II низкой ступени (5-я группа) исторически появилась раньше «VI шубертовой» ступени и тональности (4 группа). Точно так же вызывает недоумение, что тональность двойной доминанты отнесена к шестой (отдаленной хроматической) группе. Главное же заключается не в этих частностях (как бы они ни были важны сами по себе), а в том, что система в целом уже не имеет почти никакого отношения к самому понятию степеней родства в его первоначальном смысле. Ибо постепенная модуляция, например из мажора в мажорную тональность III ступени, то есть в тональность четвертой группы родства, не требует прохождения через тональности второй и третьей групп. Даже в тональность шестой группы (тональность двойной доминанты) можно совершить постепенную модуляцию, не затрагивая ни одной из предыд
Поиск по сайту: |
 пропущена тональность третьей степени родства (по классификации, данной в рассматриваемом учебнике), а в модуляции
пропущена тональность третьей степени родства (по классификации, данной в рассматриваемом учебнике), а в модуляции 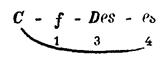 — второй. Не вступает ли это в некоторое противоречие со смыслом самого понятия постепенной модуляции как модуляции «по степеням»? Не приводит ли к чрезмерным логическим и практическим сложностям положение, при котором тональность, близкая к строю первой степени родства, сама оказывается иногда в третьей степени родства к исходной:
— второй. Не вступает ли это в некоторое противоречие со смыслом самого понятия постепенной модуляции как модуляции «по степеням»? Не приводит ли к чрезмерным логическим и практическим сложностям положение, при котором тональность, близкая к строю первой степени родства, сама оказывается иногда в третьей степени родства к исходной: