Формалізація та перероблення якісної інформації.Нечіткі множини

Якісний аналіз – один з важливих і визначальних етапів системного аналізу, це: збирання, систематизація, формалізація та переробка якісної інформації. Типові ситуації:

- попереднє вивчення складного процесу та формування мети дослідження;

- вибір найбільш важливих ефектів та характеристик (показників) процесу;

- аналіз експериментальних даних з точки зору відповідності реальному процесу;

- оцінка функціонування складних систем;

- прийняття рішень в умовах невизначеності та в нечітко визначених ситуаціях і .д.

Якісна інформація виражається за допомогою звичайної мови, але має нечіткий, наближений характер. Для використання комп’ютерних технологій необхідно співставити словесним термінам кількісні оцінки для формалізації даних та використання математичних методів обробки.

Якісний етап системного аналізу має два аспекти – смисловий та математичний. Смисловий – збирання, оцінка достовірності, систематизація та формалізація інформації. Часто якісна інформація, її достовірність суттєво залежить від психічних та фізіологічних можливостей людини. В свідомості людини формується концептуальна модель як уявлення про стан та особливості об’єкта досліджень.

Формалізація якісної інформації базується на експери-ментальних даних, які дозволяють співставити нечіткі уявлення та числові множини. В загальному випадку залучаються експерти, а в самому простому вважають, що множина Х складається з двох елементів {0,1}, наприклад “хороша” чи “погана” продукція. Так же технологічні параметри – “високий”, “низький” і т.д., але кожному з них відповідає своє числове значення.

Математичний аспект якісного аналіза полягає в відображенні якісних уявлень в математичні об’єкти.

Наприклад, коли об’єкт характеризується двома координатами стану Х₁ і Х₂, то можна прогнозувати величину Х₂ при фіксованих значеннях Х₁, а саме: “Якщо зміна величини Х₁ велика, то зміна величини Х₂ значна, в противному випадку Х₂ змінюється мало”. Терміни “велике”, “значне”, “слабке” потрібно формалізувати. Технологічні параметри ТК та підсистем складають групи:

- вимірювані автоматично (температура, тиск, рівень, інш.). Людина-оператор може на основі цих параметрів прогнозувати зміни параметрів в неконтрольованих точках, використовуючи нечітку інформацію;

- параметри, які описуються словесними (нечіткими) термінами, а для їх переводу в числовий вид приймає участь людина – експерт (наприклад, якість продукції як інтегральна оцінка).

Передбачається, що формалізація якісної інформації базується на існуванні відповідності між нечітко визначеними характеристиками та математичними об’єктами. Для першої групи параметрів це очевидно, величині параметра ставиться у відповідність числова координата в становленим початком координат та мірою, а величина параметра може описуватись словесно.

Для параметрів першого типу елемент х_iÎX – конкретні величини (наприклад температура). Кількісною характеристикою х_iÎX є елементи u_j ÎU. Множина U – діапазон зміни параметрів х_iÎX. При словесному описуванні парі (х_i, u_j) ставиться у відповідність нечіткий термін q_k ÎQ (Q – множина нечітких термінів). Нечіткі терміни, це – “високий”, дуже “високий”, “низький”, “далеко”, “близько”… На вибір цих термінів значний вплив справляє вибір опорної (реперної) точки – як правило для номінального режиму.

При класичному підході до управління не приймаються до уваги такі фактори як неясність, невизначеність, нечіткість чи неточність, а саме вони є головними в реальному житті, для складних систем. Теорія нечітких множин Л.Заде дала схему розв’язання проблем, в яких суб’єктивна думка чи оцінка відіграють суттєву роль при оцінці фактів неясності і невизначеності. В 1965 р. американським математиком Л.Заде була запропонована теорія нечітких або розмитих множин, яка отримала назву нечіткої логіки. Ця теорія дала схему розв’язання проблем, в яких суб’єктивні думки або оцінка відіграють суттєву роль при оцінці фактів неясності або невизначеності.

Автор теорії нечітких множин стверджував: “…при зростанні складності точні твердження втрачають значущість, а значущі твердження втрачають точність”.

В технічній літературі нечітка логіка отримала назву від терміну “Fuzzy-Logic” (Фуцці-логіка).

Теорія нечітких множин пройшла шлях від розробки формальних засобів представлення погано визначених понять, які використовуються людиною, та апарату для їх обробки до моделювання наближених міркувань, які використовуються людиною в повсякденній діяльності, та до створення комп’ютерів з нечіткою логікою.

Перевага підходу нечіткої логіки перед класичними методами, при описуванні систем управління полягає в тому, що при цьому можна не використовувати аналітичних залежностей. В багатьох випадках достатньо лише професійного опису того, як процесом керує досвідчений оператор (без залучення математичних, хімічних і т.д. залежностей). Нечітка логіка – перша теорія, яка оперує неточними та не зовсім ясними поняттями. Передбачається, що в більшості випадків ситуація оцінюється приблизно, а не точно.

Цей підхід появився об’єктивно тому, що при ускладненні систем зменшується можливість робити точні та значущі твердження відносно поведінки системи і наступає межа, за якою точність та значущість стають взаємновиключаючими характеристиками. Тоді вводяться спеціальні позначення (мітки), які визначають більш-менш нечіткі поняття.

U – універсальна множина (довільний набір об’єктів чи математичних конструкцій);

A – кінцева підмножина U з елементами U₁, U₂, … U_n

Тоді: _,

, - кінцева множина впорядкованих пар;

де - міра членства, функція належності, яка показує степінь належності елемента цій множині.

Якщо всі {0, 1}, тобто дорівнюють 0 чи 1, то це звичай-на (чітка) множина. Якщо може приймати значення в інтервалі від 0 до 1, тоді А – нечітка (розмита) множина. Тоді:

=0, елемент не належить множині;

=1, U;

- визначає степінь належності множині U ,

тоді А – розмита множина

В розмитій логіці значення істинності може бути розмитою підмножиною будь-якої впорядкованої множини. Практично це розмита підмножина на інтервалі [0,1], тобто точка цього інтервалу. Лінгвістичні критерії істинності – “правильно”, “не зовсім правильно” можна інтерпретувати як мітки розмитих множин. Це відповідає природній мові, в якій більшість предикатів розмиті, а не чіткі. Тоді виникають модифікатори предикатів (“дуже”, “більш-менш”, “цілком” і т.д.), які відіграють важливу роль в генеруванні значень логічних змінних: “дуже високий”, “більш-менш важливий ”і.т.д.

В класичних логічних системах є два квантори: існування та загальності. В розмитій логіці додатково до них використовуються квантори “декілька”, “головним чином”, “майже завжди”, “часто”… В розмитій логіці розмитий квантор інтерпретується як розмите число чи розмита пропорція

Приклад: ріст людини. Для поняття “високий” визначено функції залежності:

Ріст, м	m (Ui)
0,4   0,2 0,8 0,6 2,2 2,1 2,0 1,9 1,8 1,7 1,6	1,0 1,0 0,8 0,6 0,4 0,2 0,0

0

-0,2 0 1,2 1,4 1,6 1,7 1,8 1,9 2 2,1 2,2 м

Рис.4.1. Розмита множина при визначенні росту

Лінгвістична змінна – це така змінна, яка задається на кількісній шкалі і приймає значення у вигляді слів та словоутворень природної мови. Окреме значення лінгвістичної змінної або лінгвістичне значення називається термом і задається за допомогою функції належності тобто кожному терму відповідає нечітка множина. Значення лінгвістичної змінної (ЛЗ) описується нечіткими змінними. Лінгвістичні змінні (ЛЗ) використовуються для якісного словесного опису кількісної величини. Будь-яка ЛЗ та всі її значення зв’язані з конкрет-ною кількісною шкалою (базовою шкалою). Приклад базової шкали для оцінки степені руйнування об’єкта:

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

немає

незначне помірне сильно катастрофічне

Масштаб шкали може бути довільним.

Для віку:

Т(вік)={молодий, старий, дуже молодий, більш-менш молодий…}

Кожний елемент (терм) цієї множини може виражатись через розмиту множину, наприклад:

m (U_i)

молодий не дуже молодий більш-менш старий

1,0

дуже

молодий старий

0,5

30 60 вік

Рис.4.2. Функції належності

Значення лінгвістичних змінних можуть задаватись не лише базовою шкалою, а й функцією. Наприклад, функції належності допустимих лінгвістичних термів можна задати функцією: , (4.1)

a та константа в чисельнику залежить від характеру лінгвістичної змінної. Так для значення “високий” функція має вигляд:

, (4.2)

а “досить високий”: , (4.3)

“майже високий”: , (4.4)

“середній”: ,

“досить низький”: , (4.5)

Для управління на базі нечіткої логіки (фуцці-управління) характерним є безпосереднє застосування експертних знань, які формуються якісно, для генерування необхідних впливів на об’єкт. Знання щодо взаємодії з процесом за цією методикою подаються у формі правил виду:

ЯКЩО (початкова ситуація), ТО (відповідна реакція)

Така логічна конструкція відповідає природній поведінці людини в конкретній ситації, наприклад:

ЯКЩО (температура висока), ТО (зменшити дещо подачу пари)

Або:

ЯКЩО (температура висока) ТА (швидкість зростання температури значна), ТО (припинити подачу пари).

Використовуючи функції належності, можна записати такі вирази:

М=m₁|х₁+ m₂|х₂+…, (4.6)

де М – сукупність об’єктів, які належать основній множині Х;

Х- об’єкти множини М.

Цей вираз – не алгебраїчна сума, а лише визначає, що елементи Х_і відносяться до множини М з функціями належності m_і. Це може бути формою запису математичної моделі в нечіткому середовищі. Можна записати також:

М=|( х₁,m₁), (х₂,m₂)…, (х_і,m_і) | (4.7)

По аналогії із звичайними множинами в нечіткій логіці формуються основні операції над множинами А та В

- множина логічного об’єднання

С=А U В (АБО):

μ_с(х)=max (μ_А(х), (μ_В(х)); (4.8)

- множина логічного перетину (ТА)

С=А ∩ В:

μ_с(х)=min (μ_А(х), (μ_В(х)); (4.9)

- множина логічного доповнення (НІ)

С=А:

μ_с(х)=1-μ_А(х); (4.10)

Головною операцією нечіткої логіки є процедура нечіткого висновку, за допомогою якої з нечітких умов отримують наближені рішення (розв’язки). Процедура нечіткого висновку заснована на операції логічного слідування (імплікації), яка використовується в традиційній математичній логіці.

Імплікація дозволяє формалізувати знання експерта за формою “якщо А, то В”, де: А – передумова, В – висновок. Стосовно нечіткого управління Х –базова множина значень х регульованої змінної (координати). Тоді Х- базова множина х, А – множина значень х; U – базова множина значень управлінь u, В –множина значень u.

В залежності від способу отримання логічних висновків з нечітких правил можуть бути різні регулятори. Для промислового використання частіше використовується алгоритм нечіткого регулятора Мамдані, коли регятор формує чітке однозначне управління за допомогою процедури дефазифікації.

Початковими даними для такого алгоритму є:

- антецеденти n правил А₁₁,₁₂... А_1n, А₂₂...А_2n, А_n2...А_nn, які відповідають функціям належності μ і зв’язані логічними операціями кон’юкції (∩), диз’юкції (U) чи інверсії ( );

- висновок n правил В₁, В₂... В_n з відповідними функціями належності;

- конкретні значення х , х ... х вхідних змінних х₁, х₂...х_m.

В результаті необхідно отримати управління U , для чого:

- за допомогою основних операцій визначають значення істинності передумов n правил

µ_А1(х , х ... х ), µ_А2(х , х ... х )...µ_Аm(х , х ... х_m); (4.11)

- враховується, що у відповідності з основним правилом логічного висновку істинність висновку В не може перевищувати істинність передумови А, тому µ_В(U) обмежується зверху на рівні µ_А(х ):

µ_В (U)=min{µ_А1(х ,... х ), µ_В1(U)}

х Î А

µ_В (U)=min{µ_Аn(х ,... х ), µ_Вn(U)} (4.12)

- здійснюється агрегування кількох правил “ЯКЩО...ТО...” шляхом максимізації функцій належності всіх об’єднуваних правил. В результаті функція належності управляючого діяння буде:

µ_Вp (y)=max{µ_Bj (U)}, j Î (1,n); (4.13)

- здійснюють процедуру дефазифікації для знаходження конкретного значення управління. Серед різних методів найбільш розповсюдженим є метод центра ваги, коли

у = , (4.14)

Таким чином дефадзифікація – процедура генерування управлінь.

Це управління на виході фуцці-контролера (нечіткого регулятора) отримують як нечітку множину в формі функцій належності.

Метод центра ваги передбачає, що управління обчислюється як значення абcциси центра ваги площини, яка утворена функцією належності та віссю абцис.

Функції належності

Вибір виду функцій належності та їх параметрів значною мірою визначається досвідом, інтуїцією та іншими суб’єктивними факторами, в тому числі особою, яка приймає рішення – (ОПР). Тут саме і виникають нові невизначеності суб’єктивного характеру.

Приклади.

-

а х

0

.

m(х)= (4.17)

а₁ а₂

- функції степенів належності твердження “величина х велика”

μ (4.18)

х

а

μ

(4.19)

х

α α+1/к

- функція степенів належності твердження “величина |х| мала”

μ

m(х)= (4.20)

х

-α α

Те ж, “величина |х| велика”

μ

m(х)= (4.21)

х

-α α

Функція степенів належності може задаватись:

- самостійно дослідником, на основі власного досвіду; - в простому випадку;

- із залученням експертів, обробкою іх оцінок – для складних та відповідальних випадків.

Важливість використання логіко-лінгвістичних змінних обумовлена причинами:

- не всі критерії оптимізації можуть задаватись кількісно;

- між рядом параметрів, які впливають на функціонування АТК, не вдається встановити точних кількісних залежностей;

- процес оптимізації в АТК – багатокроковий, а зміст кожного кроку не завжди можна визначити однозначно;

- існуючі способи опису самих АТК (їх структури) та процесів в них – дають громіздкі залежності, їх важко або неможливо використовувати;

- в змінюваних умовах зовнішнього середовища та властивостей АТК утруднюються процеси адаптації, тим більше, що окремі підсистеми мають активну природу, тобто є людино-машинними.

Процедури завдання дослідником функції належності в нечітких підмножинах:

- визначається діапазон зміни величини параметра х Î Х з множини Ω;

- знаходять відображення φ: Ω→U, де U Î [0,1]. В якості φ може бути використане будь-яке перетворення, зокрема лінійне;

- величина параметра х Î Х описується словесно множиною термінів Q, наприклад Q^Δ= {високий, дуже високий, не високий, низький, дуже низький і.т.д.}. Потрібно, щоб в Q були відсутні терміни – синоніми, в противному випадку проводять їх класифікацію у відповідності з термінологією, яка існує в цій галузі (температура 120⁰ в цукровій промисловості – висока, в металургії – дуже низька);

- на множині Q вводиться термін q₀ Î Q – “норма”, а відносно нього симетрично визначається терміном q_к Î Q, к=1,n та протилежні ім за смислом q_e Î Q, e=1,n;

- функції належності μ_j(U), j=1, (2n+1), встановлюють відповідність Q→U з точністю до якісних відмінностей первинних термінів та прийнятих операцій над нечіткими множинами;

- термін “норма”, тобто q₀ Î Q і u₀ Î U визначає і форму функції μ(U), а також вимагає виконання таких асимптотичних властивостей:

lim μ(U)=a; lim(U)=b (4.22)

U→0 U→1

a, b – постійні для даного терміна.

μ(U)

1

0,5

U

U_а U₀ U_b 1

Рис.4.3. Функція степені належності μ(U), яка формалізує термін «високий»

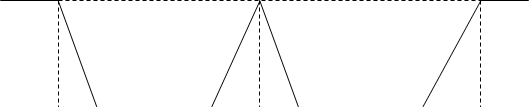
U₀ – опорний елемент U₀ Î U, який відповідає поняттю “норма”. Як правило – це 0,5 ( μ(U₀)=0,5). Звичайно, тут є значний суб’єктивізм відносно вибору U₀

Умова lim μ(U)=0 означає, що елементи U‹ U₀ в меншій степені

U→0

можна віднести до терміну “високий”, чим U₀.

Умова lim μ(U)=1 показує, що для U › U₀ степінь належності до

U→1

терміну “високий” зростає.

Нечітка множина, яка формується, вважається нормальною при

sup μ(U)=1 (4.23)

u Î U

Враховуючи асимптотичні властивості функції μ(U), дослідник може встановити інтервали [0,U_a] та [U_b,1], на яких функція задається чітко класифікацією

μ(U)= (4.24)

Найскладніше задати μ(U) при U Î[ U_a, U_b]. На цьому інтервалі для будь-якого U Î[ U_a, U_b] дослідник задає μ(U) в залежності від різниці (U-U₀) з урахуванням знаку. Приймається, що функція μ(U) є монотонною, а розриви можуть бути за умови, що в процесах трапляються “катастрофи”, тобто система стає нестійкою.

Для визначення функцій степені належності експертами рекомендуються такі процедури:

1.Виділення точки u₁ Î U на універсальній шкалі, яка, за думкою експерта, точно відповідає нечіткій множині. В цьому випадку μ(U₁)=1. Це розглядається на випадок, коли для формалізації термінів приймаються три елементи U_i(і=1,3) універсальної множини U. Для зменшення психологічного навантаження на експерта кількість термінів необхідно зменшувати. На рис. – спосіб завдання функцій належності, за допомогою яких формалізуються поняття “низький”, “середній”, “дуже високий”.

μ( U) μ( U) μ( U)

u u u

U₁ U₃ U₂ U₁ U₃ U₂ U₁

μ₁ – “низький” μ₂ – “середній” μ₃ – “дуже високий”

2.Знаходження на універсальній шкалі зліва та справа від U₁ точок, які, на думку експерта, не можна відносити до цього терміну. Це точки U₂ та U_3, для яких μ(U₂)= μ(U₃)=0.

3. Графічна побудова функцій за обраними точками при умові лінійної апроксимації.

4. Виділення підмножини U₁ ≤ U, на якій визначена формалізація терміну, U₁=[ U_{2 ,}U₃]. Часом точки U₂, U₃ можуть відноситись в нескінченність.

Це – один з найбільш простих способів.

При управлінні технологічними установками діапазон зміни кожного параметра задається відрізком (технологічні параметри – нечіткі підмножини деяких універсальних множин)

х_і=[a_i^min, а_і^max]; у_і=[b_j^min, d_j^max]

кожен з відрізків розбивають на інтервали, наприклад:

a_i^min=a_i1 ‹ a _i2 ‹...‹ a_ik= а_і^max

Значення величини параметра, яке знаходиться в одному з інтервалів, словесно характеризують термінами “малий”, “середній”, “великий”. Тоді функція належності в нечітких підмножинах, які формалізують прийняті терміни, описують залежністю:

μ(х_і)=exp(-Q_i| x_i - a_ip¹|) (4.25)

Q – постійна величина, яка знаходиться при ідентифікації функції належності:

а_ір¹=(а_іr+ а_іr+1)/2

Приклад

Параметр	Діапазон зміни	Термін, інтервал дискретизації	Функція
Витрата, м3/с	70-110	мала: 70 - 80   середня: 80 - 90   велика: 90 - 110	exp(- ) exp(- ) exp(- )
Температура, 0С	480-490	мала: 480 - 482,5   середня: 482,5 - 485   висока: 485 - 490	exp(- ) ...| y1 - 483,75|   ...| y1 - 487,5|

Поиск по сайту: