 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Процедури та алгоритми координації
Якщо для координуємих підсистем відомі критерії опти-мальності і вони мають вигляд інтегральної функції
то самим простим шляхом управління ТК є адитивна функція згортки
В цьому випадку повинна виконуватись вимога, щоб критерії Ii були однієї розмірності, або якщо вони різної розмірності, то їх можна штучно нормалізувати. Вважають, що для кожної підсистеми існує критерій управління, який має техніко-економічну природу, тоді їх сума не викликає сумнівів. Часто критерій Ітк подають у вигляді
тоді αi характеризує “вагу” конкретного критерію, тобто його значущість, і може умовно надавати можливість додавати критерії різної розмірності. В задачах координації підсистем ТК використовуються ітераційні алгоритми. При технічній реалізації алгоритмів використовуються такі процедури: 1. Рішення задачі координації повинно гарантувати розв’язок загальної задачі управління ТК в результаті розв’язання підзадач нижнього рівня, тому процедури координації необхідно визначати, виходячи із загальної мети та показників ефективності роботи ТК в цілому. 2. Для формування процедур координації необхідно мати адекватні математичні моделі підсистем, або використовувати процедури їх ідентифікації в умовах існуючих збурень. 3. Задача управління ТК в цілому є складною, і навіть за умов використання сучасних ЕОМ та обчислювальних мереж, часто доцільно отримувати часткові рішення в умовах дефіциту машинного часу. Це може бути проміжна ітерація, рішення на якій забезпечує суттєве підвищення ефективності роботи ТК. За цих умов в будь-якій точці допустимої області значень змінних необхідно визначити оцінки змінних взаємодії підсистем в напрямку найбільшого зростання показника ефективності ТК. Основними особливостями таких процедур координації є: 1. На кожній ітерації передбачається найбільше зростання показника ефективності ТК в умовах урахування зв’язків між підсистемами. 2. Проміжні результати на кожній ітерації задовольняють існуючим обмеженням і можуть бути основою для визначення управлінь, які відповідають кращим значенням загального показника ефективності ТК в порівнянні з попередніми ітераціями. 3. Задача координації для ТК розв’язується на основі математичних моделей підсистем, тобто не потрібна складна та громіздка модель для ТК. 4. Необхідно враховувати, що ітераційний процес координації в загальному випадку забезпечує досягнення лише локальних екстремумів загального показника ефективності. В той же час для складних ТК навіть цей режим дає значний ефект.


так
ні
Рис.5.3. Блок-схема алгоритму управлін- ня ТК з розв’язуванням задач оптиміза- ції підсистем та координації їх роботи.
На рис.5.3. показано блок-схема ітераційного алгоритма координації підсистем ТК. Цей алгоритм враховує попередні вимоги до процедур координації працює таким чином: 1. Для кожної з підсистем визначається набір координат стану та змінних взаємодії довільно, виходячи з обмежень в межах технологічного режиму. 2. Незалежно одна від другої розв’язуються локальні задачі оптимізації підсистем з використанням даних, які отримано в п.1. Передбачається, що для кожної з підсистем існує задача оптимізації зі своїми критеріями, моделями та обмеженнями. 3. При існуючих обмеженнях та математичних моделях визначається функція ефективності для всього ТК. 4. Формується вектор змінних взаємодії підсистем. 5. Оцінюється функція ефективності ТК з отриманими значеннями змінних взаємодії підсистем. 6. Перевіряються умови зупинки процедур координації. Якщо ІТК(n) - ІТК(n-1) £ e (n – крок ітерації, e - константа), робота алгоритма припиняється. 7. При невиконанні умови п.6. здійснюється нова ітерація, в противному випадку змінні взаємодії підсистем вважаються оптимальними. Використання наведеного алгоритму має ряд особливостей. Для прискорення процесу збіжності доцільно в кожній наступній ітерації крок змінних взаємодії зменшувати вдвічі. При практичній реалізації алгоритмів координації необхідно враховувати, що математичні моделі та функції мети для кожної з підсистем ТК є функціями багатьох змінних, часто невипуклими, що затруднює попередню оцінку збіжності цих алгоритмів. Як було показано раніше, головною умовою використання цих алгоритмів є коректність загальної задачі управління ТК.
jі=jі (Uі, Yі), і=(1,N) (5.4) та математичні моделі
неперервні на множині значень аргументів Uі Значно впливає на реалізацію алгоритмів координації і наявність обчислювальних похибок. Крім того, точне рішення задачі можливе лише при нескінченному числі ітерацій. Оцінюючи стійкість алгоритма, вважають, що існує таке число x, якого не перевищують обчислювальні похибки, що не змінює збіжність алгоритма. При реалізації алгоритмів координації обчислювальні похибки виникають при: - знаходженні екстремумів функцій мети jі (Uі, Yі); - реалізації математичних моделей; - визначенні комплексу змінних взаємодії підсистем Yі. При розробці та реалізації алгоритмів координації для конкретних ТК виникає ряд додаткових особливостей та умов. Так, наведений алгоритм розроблено в припущенні, що для кожної з координуємих підсистем виконується умова: dim Uі ³ dim Yі (5.6) Для різних ТК ця умова в загальному випадку не виконується (кількість управляючих діянь менша кількості вихідних змінних взаємодії підсистем). Це може призвести до того, що підзадачі нижнього рівня будуть некоординуємими відносно координатора, оскільки в цих підсистемах управління Uі буде однозначно визначатись вхідними та вихідними змінними. При управлінні такими ТК можна використовувати метод цін. В цьому методі координуючими діяннями є множники Лагранжа, а підзадачі нижнього рівня полягають в оптимізації модифікованої функції мети підсистеми як по управляючим діянням, так і по вхідним змінним підсистеми. В той же час область застосування такого підходу суттєво обмежена класом функцій, які описують підсистеми, а також умовами існування сідлової точки функції Лагранжа. Може виникнути також ситуація, коли при розв’язанні задач великої розмірності в реальному часі результатами на проміжних ітераціях будуть неузгоджені змінні взаємодії, що не приводить до покращення роботи координуємих підсистем. Постановка задачі координації та її реалізація виконується при обмеженнях на управляючі діяння:
що визначає допустимий діапазон зміни Uі за конструктивними та технологічними умовами. При розв’язанні задачі координації можливий випадок, коли змінні будуть на межі області. Для цього випадку необхідно додатково дослідити умови координуємості та сумісності. Таким чином, алгоритми координації для ТК повинні враховувати такі вимоги: - розв’язок загальної задачі повинен бути результатом рішення ряда відносно простих підзадач, що дає можливість подолати труднощі, пов’язані з великою розмірністю задачі; - при використанні ітеративних алгоритмів координації кожна наступна ітерація покращує показники ефективності функціонування ТК, що дає можливість управління в реальному часі та зменшує витрати машинних ресурсів; - алгоритми координації повинні використовувати, по можливості, лише один нижній рівень математичних моделей підсистем ТК, що суттєво спрощує процедуру ідентифікації цих моделей. Для агрегуванння та дезагрегування змінних в загальній задачі управління ТК використовуються прості допоміжні залежності: - при реалізації алгоритмів координації повинен бути незначним вплив еврістичних прийомів. Суттєво впливає на ефективність алгоритму і вибір методу оптимізації. Для запобігання “зависання” в численних ітераціях для пошуку оптимального рішення при визначенні режимів роботи підсистем рекомендуються модифікований метод Бокса та симплексний метод Нелдера-Міда, для знаходження глобального критерія - метод приведеного градієнта. [1,c. 86-97, 2, c.218-245]
Контрольні питання 1. Сформулюйте постановку задачі координації підсистем в складній системі управління 2. Які існують принципи координації? 3. В чому полягають умови сумісності підзадач в ієрархічній системі? 4. Як відбувається координація в двохрівневій системі 5. Що таке процедури координації? 6. Охарактеризуйте ітераційний алгоритм координації 7. Наведіть приклад координації функціонування підсистем технологічного комплексу 8. Як визначається кількість підсистем технологічного комплексу в задачі координації?
Поиск по сайту: |
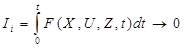 (5.1)
(5.1) (5.2)
(5.2)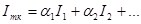 (5.3)
(5.3)





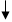

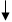
 В першу чергу необхідно оцінити існування розв’язку задачі координації. Якщо для всіх підсистем ТК функції мети
В першу чергу необхідно оцінити існування розв’язку задачі координації. Якщо для всіх підсистем ТК функції мети уі=fі (Uі, Yі), і=(1,N) (5.5)
уі=fі (Uі, Yі), і=(1,N) (5.5) Yі та в цій області існує хоча б одне рішення задачі управління підсистем, то в цьому випадку існує і розв’язок загальної задачі управління ТК. Це випливає з теореми про існування оптимального дискретного управління. Крім того, коли при реалізації алгоритмів координації значення одного з параметрів виходить за межі обмежень, формуються повідомлення та зупиняється робота алгоритма.
Yі та в цій області існує хоча б одне рішення задачі управління підсистем, то в цьому випадку існує і розв’язок загальної задачі управління ТК. Це випливає з теореми про існування оптимального дискретного управління. Крім того, коли при реалізації алгоритмів координації значення одного з параметрів виходить за межі обмежень, формуються повідомлення та зупиняється робота алгоритма. Uі min £ Uі £ Uі max і=(1,N) (5.7)
Uі min £ Uі £ Uі max і=(1,N) (5.7)