 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ентропія та її змінювання в складних системах
При вивченні сигналів в каналах систем (чи просто в системах) прешим специфічним поняттям є невизначеність випадкового сигналу, для якої введена кількісна міра – ентропія. Наприклад: якщо деяка подія може відбутись з вірогідністю 0,99 (тобто не відбутись з вірогідністю 0,01), а для іншої події ці оцінки 0,5 та 0,5, то для другого випадку краще утриматись від прогнозів- велика невизначеність. Міра невизначеності повинна бути числовою характерис-тикою, функціоналом від розподілення. Для об’єкта А з кінцевою множиною можливих сигналів А1,…Аn з відповідними ймовірностями р1,…рn мірою невизначеності приймають ентропію.
р-щільність розподілення для випадкової величини. Властивості функціонала (як міри невизначеності): 1.Н(р1, …рn)=0, лише тоді, коли будь-яке одне з Це відповідає випадкові, коли результат можна передбачити наперед з повною достовірністю, тобто коли відсутня будь-яка невизначеність. У всіх інших випадках ентропія позитивна (додатня). Ця властивість перевіряється безпосередньо. 2. Н(р1,…….рп) сягає найбільшого значення при р1 = р2 =…= рn = 3. Якщо А і В - незалежні випадкові об’єкти, то (А∩В) = Н(А)+Н(В) (7.9) 4. Якщо А і В - залежні випадкові сигнали то: Н(А∩В)=Н(А)+Н(В|А)=Н(В)+Н(А|В), (7.10) де умовна ентропія Н(В|А) визначається як математичне сподівання ентропії умовного розподілення. 5. Існує нерівність: Н(А)³Н(А|В), (7.11) що узгоджується з інтуітивним уявленням про те, що знання стану об’єкта В може лише зменшити невизначеність об’єкта А, а якщо вони незалежні, то залишить її незмінною. Цікава особливість: для оберненої задачі, тобто при бажаних властивостях міри невизначеності знайти функціонал з вказаними властивостями – лише умови 2 та 4 дозволяють розв’язати задачу однозначно (з точністю до постійного множника). Диференційна ентропія: дає можливість узагальнити міру невизначеності на неперервні випадкові сигнали:
Це аналог ентропії дискретної величини, але умовний, відносний. Смисл: начебто порівнюється невизначеність випадкової величини з щільністю розподілення р(х) з невизначеністю випадкової величини, рівномірно розподіленої в одиничному інтервалі, тому h(x) на відміну від Н(х) може бути не тільки додатньою. Міняється також h(x) у випадках нелінійних перетворень шкали х, що в дискрентному випадку значення не має, решта - аналогічно. Практичне використання: якщо при деяких обмеженнях на випадкову величину необхідно задати конкретне розподілення, то використовується принцип максимума ентропії: із всіх розподілень, які відповідають існуючим обмеженням, рекомендується обирати ті, які мають максимальну диференційну ентропію. (Тобто максимум ентропії гарантує найбільшу невизначеність, пов’язану з тим, що ми маємо справу з найгіршим випадком за даних умов). Для випадкового процесу з дискретним часом та дискретною кінцевою множиною можливих станів ентропія пов’зана з його фундаментальними властивостями. Назвемо кожен стан процеса символом, множину можливих станів - алфавітом, їх число m-об’ємом алфавіта. Число можливих послідовностей довжини n дорівнює m n, а появу конкретної послідовності можна розглядати як реалізацію однієї з m n подій. Знаючи ймовірності символів та умовні ймовірності появи наступного символа, якщо відомий попередній (у випадку їх залежності) можна обчислити ймовірність P(c) для кожної послідовності C. Ентропія множини
Для стаціонарного випадкового процеса ентропія
На множині
а математичне сподівання цієї функції
Тоді,
Ця залежність цікава сама по собі, але вона є проявом більш загальної властивості дискрентних ергодичних процесів: - не лише Для ергодичних випадкових процесів можна сформулювати ряд наслідків: 1. Незалежно від ймовірності символів і статистичних зв’язків між ними, всі реалізації високоймовірної групи приблизно рівноймірні. Цю фундаментальну властивість називають “властивістю асимптотичної рівнорозподіленості”. За відомої ймовірності Р(с) однієї з реалізацій групи можна оцінити число N1 реалізацій в цій групі:
2. Ентропія Нn з високою точністю дорівнює логарифму числа реалізацій високоймовірній групі:
3. При великих n високоймовірна група звичайно охоплює лиш малу долю всіх х реалізацій (за вийнятком випадку рівноймовірних та незалежних символів, коли всі реалізації рівноймовірні і Н=log m ). Існують об’єктивні закони змінювання ентропії в складних системах будь-якої природи, одним з яких є зростання та зменшення ентропії - зміна невпорядкованості, хаосу (стану, коли поведінка будь-якого елементу системи не залежить від поведінки решти елементів і кожного зокрема). Цей закон визначає стан організованості системи будь-якої природи, що однозначно пов’яза-но із степенем відкритості системи a. В повністю закритій системі (a=0) немає взаємодії з іншими системами та зовнішнім середовищем щодо обміну інформації. Це з часом обов’язково призведе до збільшення ентропії, зростання безпорядку, неорганізованості та хаосу. Повністю відкриті системи (a=amax) є лише теоретичною ідеалізацією, реальні системи мають кінцеве значення відкритості (0£a£amax). Коли зростання та зменшення ентропії компенсують один одного, виникає критичний рівень організації Ек, який тим більший, чим більша степінь відкритості системи. Якщо для конкретної системи рівень організації E>Ex (це відповідає більшому значенню ентропії), то організація нижча. В процесі самоорганізації відбуваються структурні зміни в системі, збільшується організо-ваність. Важливе місце займає самоузгодження дії елементів. Системи із самоорганізацією є предметом досліджень наукової дисципліни “синергетика”. Реальні системи взаємодіють із зовнішнім середовищем та іншими системами, тому їх ентропія постійно змінюється (ентропійні коливання), що залежать від степені їх відкритості. Інтенсивність зовнішнього діяння на систему не повинна перевищувати деякого значення, після якого система руйнується (не встигає самоорганізовуватись достатньою мірою). Для тривалого стабільного функціонування будь-якої системи необхідно забезпечити оптимальне співвідношення таких показників: степені відкритості; початкового рівня організації Ео; числа елементів та підсистем.
7.4.Ентропійно-інформаційні співвідношення процесу Інформація та її характеристики безпосередньо впливають на впорядкованість системи, детермінованість міжелементних зв’язків структури. Виходячи з фундаментальних залежностей для ентропії, можна визначити такі закономірності: - при взаємодії двох підсистем А і В відбувається довільне накопичення інформації (наслідок теореми К.Шеннона), а ентропія:
Впорядкування структури, зменшення сумарної ентропії супроводжується збільшенням структурної інформації:
-якщо підсистеми не можуть взаємодіяти між собою, впорядкування системи не відбувається, а приріст структурної інформації:
Крім того, справедливий вираз:
DІs=Hmax- Нреальне=DH (7.24) тобто, кількість інформації, яка зберігається в структурі системи є різницею між значенням максимальної ентропії при одинакових і незалежних ймовірностях станів елементів, підсистем р1, р2…рn і її реальним значенням при неодинакових значеннях р1, р2…рn. Для реалізації процесу управління складним об’єктом необхідно забезпечити такі вимоги: 1. Для зменшення ентропії об’єкта з рівня Но до потрібного Нпот необхідно і достатньо, щоб кількість інформації яку отримує об’єкт, була
Якщо система управління буде передавати на об’єкт меншу інформацію І*<Іпотр, то кінцева ентропія Нк буде більшою Нпотр, а при І*>Іпотр буде Нк<Нпотр і можлива різноманітність станів об’єкта управління знизиться, а степінь його організованості підвищиться за рахунок показника впорядкованості R. Для ідеального управління Припустимо, що СУ може передавати потік інформації F *(t) за час tк. Тоді за один цикл в об’єкт вноситься кількість інформації
і Х®Хзд. Якщо діє перешкода f, то ентропія приведеної до виходу перешкоди - Нf (х)= Ff-інтенсивність перешкоди Тоді для об’єкта Н(х)=Но(х)+ Якщо Н(х)=Нпотр, то Но(х)-Н(х)=Іпотр (7.29) Тобто: Іпотр=І*-Hf (х), (7.30) а І* ³ Iпотр + Нf (х) (7.31) або
2. Якщо час управління не обмежено і Іпотр < ¥, то для встановлення заданої впорядкованості станів об’єкта управління необхідно і достатньо, щоб
Дійсно Іпотр обмежено, тому завжди можна знайти такий час управління Т, щоб
тобто можливо встановлення потрібного рівня показника впорядкованості. Наслідки: -якщо Н(х) – диференційована функція часу, то швидкість зміни ентропії об’єкта управління дорівнює різниці потоку ентропії приведених перешкод та потоку інформації, які циркулюють в контурі управління; -організація процесу збільшується тоді і тільки тоді, коли потік інформації, яка циркулює в системі, більший за утворений потік ентропії приведених перешкод. Тоді ентропія процесу зменшується. 3. Для того, щоб час управління Т був не більший заданого, необхідно і достатньо, щоб
Тпотр - заданий час встановлення потрібної статистичної впорядкованості об’єкта управління. 4. Для того, щоб СУ забезпечувала рівень впорядкованості станів (процесів) об’єкта не нижче Rпотр, необхідно і достатньо, щоб вона мала середню потужність не меншу, ніж
Ця рівність отримується з
Виконання умови 7.36 залежить від значення р. При р=0.5 умова не може виконуватись, а при р<0.5 СУ дезорганізує процес, оскільки I*(X,U)<0. Інформаційний підхід дає можливість оцінити властивості системи управління незалежно від її структури. З цих позицій цікаво розглянути класичні принципи регулювання (управління): 1. За відхіленням: ентропія регульованих змінних не може бути меншою приведеної ентропії перешкод Hf(x). Це базується на тому, що в системі використовується інформація лише про спостерігаємі зміни. 2. За збуренням: ентропія управляємої системи не може бути зменшеною. При цьому управлінні не вдається зберегти статистичну організацію системи на певному рівні. Незмінність ентропії можлива лише тоді, коли всі збурення спостерігаються, а формуємі управління настільки адекватні їм, що всі характеристики системи інваріантні відносно цих факторів- це неможливо на практиці. Не дивлячись на чудову властивість “не пропускати” збурення, цей принцип не забезпечує потрібної впорядкованості. 3. Комбінований: статистична організація процесів в об’єкті управління більш висока, чим при 1 (за відхиленням)-за рахунок введення додаткової інформації за збуренням. Можна зменшити вимоги до об’єму інформації, але ускладнюється СУ. Додаткові методи управління в ССУ: -управління з прогнозом. Використання прогнозуючої інфор-мації з урахуванням поточної та минулої (про поведінку об’єкта в різних ситуаціях) дає можливість забезпечити більш високий рівень впорядкованості при ймовірності прогнозуючої інформації Pпр>0.5 . Тут головна проблема – надійність прогнозу. -управління “з пам’яттю”. Воно можливе лише за умови , що ситуація стабільна і мало змінюється за час роботи об’єкта. При управлінні специфічною особливістю інформації є її збереженість при користуванні, що дає можливість багаторазового використання однієї і тієї ж інформації для різних цілей і дій: на відміну від речовини та енергії інформація “не розщеплюється”. При передачі джерелом І інформації множині користувачів n кожен з них приймає таку ж кількість інформації, яка видавалась джерелом. При цьому користувачі (приймачі) можуть формувати і видавати різну інформацію за змістом і кількістю І1,…Іn. [1, c.109-123, 3, c.174-245] Контрольні питання 1. Дайте визначення інформації та її значення в складних системах управління. 2. В чому полягають інформаційні бар’єри? 3. Назвіть форми проявлення інформації. 4. Класифікація та визначення видів інформації в складних системах. 5. Вимоги до інформації. 6. Дайте визначення терміну “ентропія”. 7. Властивості ентропії як міри невизначеності. 8. Як змінюється ентропія в складних системах. 9. Дайте ентропійно-інформаційні оцінки процесу управління.
Поиск по сайту: |
 (7.8)
(7.8) (решта нулі).
(решта нулі). - випадок найбільшої невизначеності. Варіація Н по рі за умови
- випадок найбільшої невизначеності. Варіація Н по рі за умови  дає рі = const =
дає рі = const =  (7.12)
(7.12) , за визначенням:
, за визначенням: (7.13)
(7.13)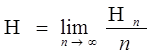 (7.14)
(7.14) , яка є випадковою. Визначимо:
, яка є випадковою. Визначимо: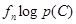 (7.15)
(7.15) (7.16)
(7.16) (7.17) (7.18)
(7.17) (7.18) при
при  має границею Н, а й сама величина fn(С) ®Н при
має границею Н, а й сама величина fn(С) ®Н при  близкість fn(С) до Н є майже достовірною подією.
близкість fn(С) до Н є майже достовірною подією. (7.19)
(7.19)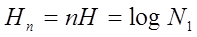 (7.20)
(7.20) управління
управління (7.21)
(7.21) >0 (7.22)
>0 (7.22) (7.23)
(7.23) (7.25)
(7.25) .
. (7.26)
(7.26)
 (7.27)
(7.27)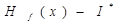 (7.28)
(7.28) (7.32)
(7.32) - середні потоки інформації управління та ентропії перешкод.
- середні потоки інформації управління та ентропії перешкод.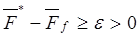 (7.33)
(7.33) (7.34)
(7.34) (7.35)
(7.35) ) (7.36)
) (7.36) (7.37)
(7.37)