 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формалізація опису структури системи на основі графових моделей
Теорія графів – розділ математики, який досліджує властивості різних геометричних схем (графів), які утворені множиною точок та ліній, що їх з’єднують. При структурному аналізі систем елементам ставлять у відповідність вершини графа, а зв’язкам – ребра (вершинний граф). Іноді зручно використовувати реберний граф (елементи – ребра, зв’язки – вершини). В подальшому будемо використовувати вершинні графи. Види графів. Якщо визначена множина елементів V, то граф G =G(V) вважається визначеним, коли деяке сімейство сполучень елементів або пар виду E=(a,b), де a,b V, вказує, які елементи є зв’язані. У відповідності з геометричною інтерпретацією пара E=(a,b) – ребро, а елементи a і b – кінцеві точки ребра, або вершини. Якщо порядок розташування вершини не має значення, то Е – неорієнтоване ребро, а якщо це важливо, то Е – орієнтоване ребро, дуга, причому а – початкова вершина, b – кінцева. В теорії графів використовують також таку термінологію: ребро Е інцидентно вершинам a,b; вершини а і b інциндентні ребру Е. Граф, складений виключно з орієнтованих ребер – орієнтований. Відповідно: неорієнтовані та змішані графи. Неорієнтований граф можна перетворити в орієнтований заміною кожного ребра Е парою ребер з тими ж кінцями, але протилежної орієнтації (процес подвоєння) Граф кінцевий, коли число ребер кінцеве, та нескінченний – у протилежному випадку. Граф, який складається лише з ізольованої вершини - нуль-граф, а граф, ребрами якого є різні пари двох різних вершин а , b і з V – повний граф. В орієнтованому повному графі є пари ребер по одному в кожному напрямку, які з’єднують будь-які дві різні вершини (а і b).
Способи формалізованого задання графів. Графічне представлення - найбільш наочне, але не достатнє, його не можна використовувати при роботі на ЕОМ. Матричне представлення. Можуть бути різні форми. Матриця суміжності вершин для неорієнтованого графа:
n – кількість вершин. Елементи аij визначаються так:
Передбачається, що нумерація вершин графа проведена. Для неорієнтованого графа матриця суміжності є симетричною. В матриці суміжності вершин для орієнтованого графа:
Елементи визначаються так:
Вид матриці суміжності орієнтованих графів суттєво залежить від принципу нумерації вершин. Матриця інцидентності:
і=1,2…n; j=1,2…m, n – кількість вершин; m – кількість ребер Для неорієнтованого графа:
Для орієнтованого графа:
Часто в практичних задачах більшість елементів в матрицях А і В є нульовим, що приводить до неефективного використання ЕОМ. Доцільним є множинні способи формалізації структури.
Множинне представлення.Для орієнтованого графа Множина G-1(i) визначає всі вершини, з яких можна безпосередньо попасти в вершину і - зворотна відповідність (відображення). По аналогії множина G-1(i) називається множиною лівих інциденцій. Множинний спосіб більш практичний, особливо для ієрархічних систем. Частинний граф та підграф. Граф H називається частинним графом графа G, якщо його множина вершин V (H) є в множині вершин V графа G і всі ребра графа H є ребрами графа G.
в г
Рис. 2.2. Структура та орієнтований граф системи а – структура системи; б – орієнтований граф; в-підграф; г – частинний граф
Граф G1(D) називається підграфом графа G(V), якщо множина вершин D є в множині вершин V і ребра графа G1 є всіма ребрами графа G, кінці яких лежать в множині D. Якщо D=V, то підграф G(D) співпадає з графом G(V). Поняття частинного графа та підграфа є основою для виділення підсистем при аналізі складних систем. Ланцюг, шлях, цикл, контур. Ланцюг – послідовність ребер E0, E1…Ek-1, Ek…, коли кожне ребро Ek-1 дотикається одним з кінців з ребром Ek. Ланцюг можна позначити послідовністю вершин, які вони містять. Наприклад, послідовність вершин (1,4,3,5), (1,3,5) – є ланцюгами. Це поняття частіше використовується для неорієнтованих графів (рис.2.3). Шлях – послідовність дуг, коли кінець кожної попередньої співпадає з початком наступної, наприклад: (1,3), (3,5), (5,1) для рис.2.3. Це поняття також використовується доя орієнтованих графів. Цикл – кінцевий ланцюг, який розпочинається і закінчується в одній вершині, наприклад: (1,4,3,1) для рис.2.3. Це поняття має смисл також для неорієнтованих графів. Контур – кінцевий шлях, для якого початкова вершина першої дуги співпадає з кінцевою вершиною останньої дуги шляху: послідов-ність дуг (1,3), (3,5), (5,1) – контур (рис.2.2).
Рис.2.3. Неорієнтований граф
Довжина ланцюга (шляху) – число ребер (дуг), які входять в лан-цюг (шлях) графа. Матриця суміжності вершин А є матрицею безпосередніх шляхів графа, які мають довжину, що дорівнює одиниці. Загальне число тран-зитних шляхів від вершини і до вершини j довжиною k можна отримати в результаті піднесення до k-тої степені матриці А: Аk=АА…А=Ак-1∙А Елемент матриці Аk аij(к) визначає кількість шляхів довжиною k від вершини і до вершини j. Степінь вершини. Число ребер, інцидентних вершині неорієнто-ваного графа, - степінь вершини ρ(і). Число дуг орієнтованого графа, які мають початковою вершиною вершину і – напівстепінь витоку вершини і ρ+(і). Аналогічно, число дуг, які мають кінцевою вершиною вершину j ρ-(j). Сума напівстепенів захода всіх вершин графа, а також сума напівстепенів витоку всіх вершин дорівнюють загальному числу дуг орієнтованого графа G(V):
m – число дуг графа; n – число вершин графа. Для неорієнтованого графа
З’язність графа. Неорієнтований граф G(V) називається слабкозв’язним (зв’яз-ним), якщо для будь-яких вершин і та j існує ланцюг з вершини і в вершину j. Орієнтований граф G(V) називається сильнозв’язним, якщо для будь-яких вершин існує шлях з вершини і в вершину j. Граф на рис.2.3.– слабко-зв’язний.
Рис.2.4. а)сильно Рис.2.4. б) незв’язний граф з двох зв’язний граф сильно зв’язних підграфів
Будь-який неорієнтований граф можна розкласти на сукупність зв’язних підграфів; будь-який орієнтований – на сукупність сильно зв’язаних підграфів.
Порядкова функція на графі, поняття рівня.Порядкова функція на графі без контурів дозволяє розбити множину вершин на підмножини, які не пересікаються, на впорядковані так, що коли вершина входить в підмножину з номером і, то наступна за нею вершина – в підмножину з номером, більшим i. Отримані підножини не пересікаються - рівні. Виділення комплексів графах.Один з перших алгоритмів заснований на операціях з матрицею зв’язності з метою виділення на графі системи, шляхів різної довжини та побудови матриці комплексів. Використання матриці шляхів на графі. Матриця є квадратною, кількість стовпців відповідає кількості елементів в складі ТК. Якщо на графі є шлях будь-якої довжини з вершини і у вершину j, то на пересіченні і-го рядка та j-го стовпця ставиться одиниця, в протилежному випадку – 0.
Рис.2.6. Структура системи Використання матриці шляхів на графі.Матриця є квадратною, кількість стовпців відповідає кількості елементів в складі ТК. Якщо на графі є шлях будь-якої довжини з вершини i у вершину j, то на пересіченні і-го рядка та j-го стовпця ставиться одиниця, в протилежному випадку – 0 (див. табл. 2.1). На основі матриці Р будується допоміжна матриця S (див. табл.2.2)
Таблиця 2.1. Матриця шляхів графа – P:
Таблиця 2.2 Допоміжна матриця S
На основі матриці S визначаються комплекси, які входять в склад графа ТК. Якщо в і-му рядку є лише один ненульовий елемент Sii (на головній діагоналі), то елемент ТК з номером і можна розрахувати окремо від решти елементів (це – 1,6). Рядки матриці S, які мають крім елемента Sii інші ненульові елементи – комплекси. Ненульові елементи показують вершини графа, які входять в комплекс. В прикладі в склад ТК входять два комплекси: комплекс 1: - 2, 3, 4, 5, 9 комплекс 2: - 7, 8. Наведений алгоритм потребує багато ручної праці. Ще один алгоритм. Розглядаються будь-які три вершини графа ТК – i, j, m. Якщо існує шлях (будь якої довжини!) з вершини і в вершину j і з j в і, то ці вершини належать одному комплексу k. Для приєднання вершини m до комплекса необхідно проаналізувати: чи є шлях з будь-якої вершини комплекса (наприклад, і), у вершину m та зворотній шлях з вершини m в будь-яку вершину комплекса k (наприклад,і). Якщо ці два шляхи існують, то вершина m належить комплексу k. Для наведеного вище прикладу виділяються комплекси: k1 (вироджений): - елемент 1 k2: 2, 3, 4, 5, 9 k3 (вироджений): елемент 6 k4 : 7,8
Поиск по сайту: |
 , (2.1)
, (2.1) (2.2)
(2.2)
 (2.4)
(2.4) (2.5)
(2.5)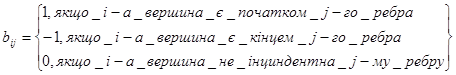 (2.6)
(2.6) (V) задається множина вершин та відповідність G, яка показує, як зв’язані між собою вершини. Відповідність G в цьому випадку є відображенням множини V в V. Для кожної вершини і відповідність G визначає множину вершин G(i), в які можна безпосередньо попасти з вершини і.Часто G(i) називають множиною правих інциденцій.
(V) задається множина вершин та відповідність G, яка показує, як зв’язані між собою вершини. Відповідність G в цьому випадку є відображенням множини V в V. Для кожної вершини і відповідність G визначає множину вершин G(i), в які можна безпосередньо попасти з вершини і.Часто G(i) називають множиною правих інциденцій.

 а б
а б






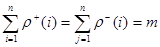 , (2.7)
, (2.7) (2.8)
(2.8)

 (2.13)
(2.13)