 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Опис процесу функціонування ієрархічної
Системи управління ТК Будемо вважати, що ТК складаються з N підсистем. Серед вихідних змінних підсистем є такі, що відображають зв'язки підсистем з навколишнім середовищем та не являються змінними взаємодії підсистем. В загальному випадку компоненти векторів X, Y, Z,U мають обмеження у вигляді нерівностей типу:
чи рівностей. При управлінні ТК враховуваться також проміжні ємності, мережі трубопроводів, тощо. Як було показано вище, загальний показник функціонування ТК на часовому інтервалі
Таким чином, критерій ефективності ТК - адитивна функція критеріїв ефективності підсистем. Для кожної з підсистем критерій ефективності можна представити в вигляді:
де:
В процесі роботи ієрархічної системи управління визначення управляючих діянь здійснюється в дискретні моменти часу при розв'язанні підзадач першого рівня
де: tmi - дискретні моменти часу, в які розв'язуються підзадачі
З урахуванням дискретизації часу математичні моделі ТК часто - записують в вигляді різницевих рівнянь:
де: Δ - достатньо малий крок дискретизації часу; у - вектор, який включає вихідні змінні підсистем: Опис динамічних об'єктів в кінцево-різницевій формі на сьогодні є загальноприйнятим, якщо векторна функція f неперервна разом з частинними похідними першого порядку. Використання кінцево-різницевої апроксимації систем диференційних рівнянь, які описують неперервні процеси, приводить до задачі нелінійного програмування, розв'язок якої в загальному випадку може відрізнятись від розв'язку початкової задачі оптимального управління неперервним об'єктом. Виникає проблема дослідження збіжності кінцеворізницевої апрокси-мації до рішення початкової задачі.
кусочно-неперервні функції, а вектор-функція f(Y(t), U(t), X(t), Z(t), t) задовольняє умові Ліпшиця стосовно своїх аргументів (як відомо, умова Ліпшиця входить у формулювання теореми про існування та єдність рішень диференційного рівняння). При
В реальних системах оперативної оптимізації неперервних об'єктів на основі кінцево-різницевої апроксимації диференційних рівнянь, які розв'язуються зо допомогою ЕОМ, величина кроку дискретизації Δ завжди має кінцеве значення (Δ≠Ο), тому розв'язок задачі завжди наближений. Вираз може набути більш простої форми в результаті переходу від інтегралу до суми:
де:
Загальна задача оптимального управління на часовому інтервалі Τ=τ полягає в забезпеченні показника ефективності в просторі управлінь Щодо функцій f, які описують управління підсистеми та залежностей - для визначення показників ефективностей, то їх можна вважати неперервними, нелінійними в області допустимих значень, що визначаються обмеженнями , та такими, що мають неперервні частинні похідні. Якщо припустити, що змінні взаємодії підсистем задані, то загальну задачу управління ТК можна представити у вигляді множини незалежних підзадач управління підсистемами ТК Таким чином, характерними ознаками підзадач підзадачі розподілені як в просторі, так і за часом; підзадачі можуть розв'язуватись незалежно одна від одної, якщо задано умови, викладені вище; постановка підзадач Для розв'язання загальної задачі Таким чином підзадачі
Розв'язок кожної з підзадач Аналогічну структуру можна отримати для ієрархічної системи з числом рівнів, більшими двох.
Поиск по сайту: |
 ,або
,або 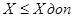 ,або
,або 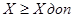
 , коли він має зміст технологічної складової прибутку, можна представити у вигляді:
, коли він має зміст технологічної складової прибутку, можна представити у вигляді: (6.6)
(6.6)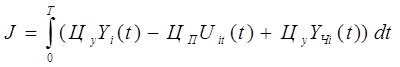 (6.7)
(6.7) - змінні взаємодії з η-οϊ підсистеми на і-ту;
- змінні взаємодії з η-οϊ підсистеми на і-ту;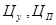 - коефіцієнти вартості, які враховують ціни потоків Υ та U.
- коефіцієнти вартості, які враховують ціни потоків Υ та U.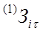 , при цьому в загальному випадку підзадачі розв’язуватися з різними періодами
, при цьому в загальному випадку підзадачі розв’язуватися з різними періодами 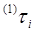 для різних підсистем комплексу {Pi},i=(l,N). Тоді показник ефективності можна записати в формі:
для різних підсистем комплексу {Pi},i=(l,N). Тоді показник ефективності можна записати в формі: (6.8)
(6.8)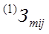 .
.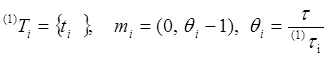
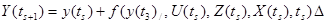 (6.9)
(6.9)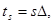
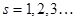 .
.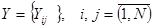 .
. Показано, що збіжність траєкторії дискретної апроксимації Y(t) до траєкторії в смислі різниці векторів
Показано, що збіжність траєкторії дискретної апроксимації Y(t) до траєкторії в смислі різниці векторів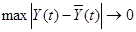 при
при 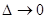 для випадку, коли U(t), Z(t) -
для випадку, коли U(t), Z(t) -  на інтервалі розв'язання задачі [0,Т].
на інтервалі розв'язання задачі [0,Т].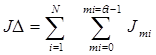 (6.10)
(6.10)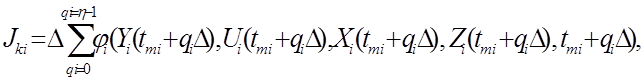
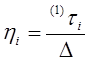 (6.11)
(6.11)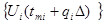 ,
, 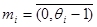 ,
, 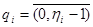 ,
, 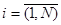 при існуючих обмеження, оцінках збурень
при існуючих обмеження, оцінках збурень  ,
, 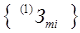 ,
, 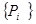 ,
,  . При цьому кожна із підзадач
. При цьому кожна із підзадач 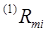 полягає в досягненні показником ефективності
полягає в досягненні показником ефективності 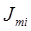 екстремуму на часовому інтервалі
екстремуму на часовому інтервалі  при існуючих обмеженнях та значеннях змінних Υ та X та оцінках збурень Ζ.
при існуючих обмеженнях та значеннях змінних Υ та X та оцінках збурень Ζ.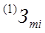 є:
є: отримана формальним шляхом на основі декомпозиції загальної задачі
отримана формальним шляхом на основі декомпозиції загальної задачі 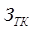 .
. підзадач
підзадач  підзадач
підзадач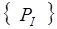 ,
,  (6.12)
(6.12) в моменти часу
в моменти часу  . Підзадача
. Підзадача 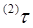 , а підзадачі
, а підзадачі 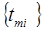 ,
, 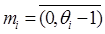 ,
, 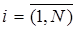 .
.