 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Моделювання технічної структури ССУ
Таку модель можна отримати, якщо використовувати орієнтовані графи, тоді граф технічної структури записується як G(V,B), де V – множина функціональних елементів Vi якщо задано G1(V1,B1) і G2(V2,B2), (2.19) то їх об'єднанням буде G1(V1,B1) U G2(V2,B2) = G3(V3,B3) (2.20) при цьому: V3 = V1 U V2 , B3 = B1 U B2 (2.21)
операція перетину: G1(V1,B1) I G2(V2,B2) = G3(V3,B3) (2.22) V3 = V1 I V2 , B3 = B1 I B2 (2.23) різниця орієнтованих графів: G1(V1,B1) \ G2(V2,B2) = G3(V3,B3) (2.24) V3 = V1 \ V2 , B3 = B1 \ B2 (2.25) Для автоматизованих ТК при описі технічної структури необхідно включити також множину технологічних елементів, тобто технологічного обладнання,.Тоді орієнтований граф технічної структури АТК буде подаватись O(I,Q)=Г(M,A) U G(V,B), (2.26) де Г(M,A) орієнтований граф технологічного об’єкта управління. При цьому М –множина технологічних об’єктів, А – зв’язки між ними G(V,B) – оргграф системи управління. При цьому необхідно враховувати, що перетин графів Г(M,A) ∩ G(V,B) =Æ (2.27) не пуста множина.
Графові моделі технічної структури складної системи управління.Якщо система реалізує множину функцій F={f1,f2,…,fm}, то кожну з функцій можна представити як відображення в підсистемі за h маршрутами { j=1, …m. Тоді модель функціональної підсистеми: Gj (Vj , Bj )=Uh Mi (Х,У) (2.28) Uh Mi (Х,У) Структура вузла управління системи – сукупність функціональних елементів Vj та зв’язків між ними Вj, а спосіб їх організації диктується реалізуємими підсистемою функціями і цілями. Вузол управління реалізує q (qÎm, q³1) функцій із заданими показниками якості. Будь-яка система чи підсистеми формалізована моделями “вхід-вихід” – розв’язувальна система. Тоді завжди є розв’язувальні елементи. В першому наближенні число вузлів управління r визначає степінь розподіленості ТС системи. Модель вузла управління (його ТС):
qÎm; xÎXj; yÎYj; Vr= Тоді модель ТС системи управління: G(V,B)=
(2.31) і=1,…h; j=1,…q; r=1,…r, qÎm r- число вузлів управління;
показниками якості; h – маршрути перетворення вхідної інформації у вихідну; m – кількість функцій системи. Наведені моделі: - наочні, добре відображають конфігурацію системи та зв’язки між елементами і їх групами; - при відомій важливоті окремих елементів можна визначити значення показників якості системи з урахуванням способів з’єднання елементів; - дозволяють перетворити графові представлення в матричні еквіваленти (матриці суміжності, дистанційні матриці…); - в той же час ці моделі громіздкі і не завжди зручні.
Поиск по сайту: |
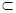 V, B – множина зв’язків між ними, В і
V, B – множина зв’язків між ними, В і 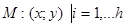 } (М – множина технологічних елемен-тів в ТК) показників вхідної інформації в показники вихідної (х Î Хj Ì Х – модулі –джерела інформації про об’єкт, yÎYjÌY – модулі прий-мачі інформації,
} (М – множина технологічних елемен-тів в ТК) показників вхідної інформації в показники вихідної (х Î Хj Ì Х – модулі –джерела інформації про об’єкт, yÎYjÌY – модулі прий-мачі інформації,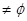 , i=1,…h; j=1,…m, хÎХj, yÎYj (2.29)
, i=1,…h; j=1,…m, хÎХj, yÎYj (2.29)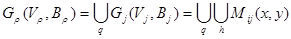
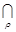 Gj
Gj 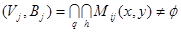 ; j=1,…q; i=1,…h (2.30)
; j=1,…q; i=1,…h (2.30)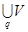 j; Вr=
j; Вr= 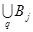
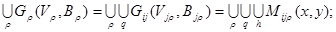
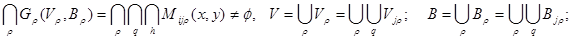
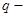 кількість реалізуємих підсистемою функцій із заданими
кількість реалізуємих підсистемою функцій із заданими