 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Агрегативні моделі функціонування великих систем управління
Основою формалізації процесу функціонування ССУ (як і інших складних систем) є положення: - будь-яка система функціонує в часі , взаємодіючи із зовнішнім середовищем, і в кожний момент часу може знаходитись в одному з можливих станів; - на вхід системи поступають (можуть поступати) вхідні сигнали; - система може видавати (формувати) вихідні сигнали; - стан системи в даний момент визначається попередніми станами та вхідними сигналами, які поступають в даний момент часу і раніше; - вихідний сигнал в даний момент часу визначається станами системи та вхідними сигналами, які відповідають даному та попереднім станам. Названі положення формалізуються таким чином: 1. Множина елементів часу, в якій розглядається функціонування системи tÎT. Множина T в загальному випадку є підмножиною В дискретному часі функціонують: кінцеві автомати; ЕОМ, МПК. В неперервному: АСУ ТП; електричні системи В дискретно-неперервному: ієрархічні СУ: на нижньому рівні – неперервні, на верхньому – дискретні. Функціонування в часі - процес переходу системи із стану в стан. Множина станів Z: - сукупність станів системи, яка визначається множиною станів елементів системи. Якщо кожен з елементів може бути в двох станах, то система з n-елементів може знаходитись в одному з 2n станів (стан дискретних автоматів, стан стосовно надійності)
- дискретні стани. Стан системи характеризується деяким невід’ємним числом Z(z=0,1,2,3…) (6.14) Наприклад – аналіз складних інформаційних систем з однією фазою обслуговування. Тоді Z – кількість задач, запитів, які находяться в системі (на обслуговуванні або в черзі). Стан системи описується набором цілих невід’ємних чисел.
Zi – число вимог в і-фазі; r - число фаз Це: динаміка багатофазних, багатоетапних систем типу теле-автоматичних систем масового обслуговування. Стан системи описується набором дійсних чисел – вектором фазових координат. В загальному випадку вважають, що стан системи Z описується деяким набором характеристик Zi: Zi Î Zi (i=1,2 …k), (6.16) Zi – задані множини, а множина можливих станів складної системи визначається як прямий добуток множин Zi: Z=Z1´ Z2 ´…´ Zi … ´ Zk (6.17) Множина станів Z системи співпадає з простором координат стану X. Тоді в кожний момент часу стан Z(t) є точка в евклідовому просторі з координатами Z1, Z2… Zk. 2. Множина вхідних сигналів uÎU0 для даного моменту U(t) tÎT. Вхідний сигнал описується набором характеристик UiÎUi (i=1,2…m), Ui – задані дискретні чи неперервні множини Прямий добуток: U=U1´ U2 ´…Ui´….Um (6.18) - простір вхідних сигналів, а сигнал U – точка простору U з координатами U1,U2 …Ui...Um Відображення u=L(t) – вхідний процес 3. Вихідні сигнали yÎY0 (Y0 – множина вихідних сигналів). Якщо вихідний сигнал y описати набором характеристик y1, y2…yi,…yn, yi ÎYi (i=1,2…n), Yi – задані множини, то прямий добуток Y= Y1 5 Y2 5…5 Yi 5…Yn - простір вихідних сигналів (y0 Ì Y)/ Можна вводити в розгляд вихідний процес y=M(t). В класі великих СУ розгялдаються системи без післядії – системи, майбутня поведінка яких визначається даним станом і не залежить від передісторії, тобто того, яким чином система прийшла в цей стан. Для детерміністських систем їх динаміка задається оператором переходів Н та оператором виходів G. Оператор переходів Н визначає динаміку переходів системи із стану в стан: Z(t)=H{t0, t, z(t0), (t,xL] z(t0) – початковий стан; z(t0) ÎZ , t0 ÎT, tÎT; { (t,xL] При фіксованих t0, z(t0), (t,xL] Сукупність впорядкованих пар (t,z) для всіх tÎT, де z визначається рухом Z=Z(t) – фазова траекторія системи. Сукупність точок простору Z, які відповідають як відображення Z=Z(t) всім t Î T – траекторія системи в просторі станів. Таким чином, вхідний процес х(t) можна розбити на окремі ділянки і аналізувати поведінку системи на кожній з них. Оператор виходів системи G визначає динаміку вихідних сигналів: Y(t)=G{t,t0,z(t0),(t,UL]
Узагальнена динаміка ССУ описується об’єднаним оператором: F=H ´ G - оператор функціонування, а сукупність точок {z(t),y(t)} простору Z´Y, які відповідають всім t Î T – траєкторія функціонування. Подібний підхід – для стохастичних систем. На введених поняттях засновано агрегативний опис процесу функціонування складних систем. Агрегат – уніфікована структура, яка характеризується множинами Т, Z, U, Y та операторами H та G. Для оцінки функціонування агрегата вводиться стан z(t+0), в який він може перейти за малий інтервал часу. Вид оператора H залежить від того, чи поступають на протязі цього інтервалу часу вхідні сигнали. Якщо в момент tS в агрегат поступає сигнал, то: Z(ts+0)=H1[ts, Z(ts), U(ts)], ts Î Т (6.21) Якщо напівінтервал (ts, ts+1] не включає жодного моменту надходження вхідних сигналів, за винятком ts+1, то Z(t)=H2[t1, ts, z(ts+0)], t Î (ts, ts+1] (6.22) З множини станів Z агрегата виділяють підмножину Z(y) для моментів видачі вихідного сигналу: у(t*)=G[t*, z(t*)] (6.23) Можливі також зміни стану в моменти видачі вихідних сигналів при виході Z(t) на межу підмножини Z(y), для чого вводиться оператор H3: z(t*+0)=H3[t*, z(t*)] (6.24) Сукупність операторів H1, H2, H3 задає оператор Н, а оператори Н та G повністю визначають модель функціонування агрегата. Тоді процес функціонування агрегата складається, в основному, з стрибкоподібних змін стану в моменти надходження вхідних сигналів на видачі вихідних сигналів (оператори Н1, Н2) та змін стану між цими моментами (оператор Н3). Прикладом такого опису функціонування може бути складна система управління щодо надходження вхідних сигналів та чергових задач. Для складних систем управління використовуються: - агрегат як випадковий процес. В моменти надходження вхідних сигналів відбувається “регенерація” вхідного процесу, який описує функціонування агрегата, тобто розвиток цього процеса та після таких моментів не залежить від його передісторії; - кусково-марківський агрегат, заснований на закономірностях марківських процесів; - кусково-неперервні агрегати, які виділяються конкретизацією множин станів, входів та виходів, а також операторів переходів і виходів; - кусково-лінійні агрегати, засновані на розв’язках диференційних рівнянь. За допомогою кусково-неперервних та кусково-лінійних агрегатів можна формалізувати різні реальні процеси: передачі та обміну даними в мережах; рух транспорту; зміни в системах масового обслуговування і т.д. В той же час представлення реальних систем у вигляді агрегатів неоднозначно, що значною мірою залежить від вибору фазових змінних. В будь-якому випадку необхідно забезпечити компроміс між точністю опису та повнотою отримуваної інформації і простотою моделі. [1, c.98-108, 3, c.67-78, 5, c.94-108] Контрольні питання 1. В чому полягає процес функціонування складної системи? 2. Які існують підходи до формалізації процесу функціонування ієрархічних систем управління? 3. Як формально відображається процес функціонування складної системи управління? 4. Охарактеризуйте структуру підзадач управління в складній системі 5. Як описується процес функціонування системи управління технологічним комплексом? 6. Як формуються агрегативні моделі функціонування складних систем? 7. Дайте визначення поняттю “агрегат”. 8. Що таке оператори переходів і виходів?
7. Інформаційні характеристики ссу 7.1. Інформація в задачах управління Історично поняття інформації пов’язане з набуттям нових знань в галузях науки: фізиці, філософії, біології, теорії зв’язку і інш. Спроби отримання об’єктивної інформації завжди наштовхуються на перешкоду, пов’язану з участю людини в експериментах, розробках моделей і т.д. В 1877 р. Л.Больцман сформулював поняття ентропії як міру невизначеності. В 1946 р. К. Шенон побудував теорію інформації і виявилось, що термодинамічна ентропія Л. Больцмана та інфор-маційна ентропія К. Шенона описуються однаковими формулами, це підкреслює той факт, що системи різної природи мають загальні властивості і закономірності, і це приводить до необхідності використання системного аналізу. Для системного аналізу в процесі управління поняття інформації розширюється і трактується таким чином: як тільки стан одного об’єкта знаходиться у відповідності до стану іншого, то один об’єкт відображає другий, тобто містить інформацію про нього. Таким чином, інформація в принципі виникає тоді, коли об’єкт змінює свій стан. Значення інформації в великих системах управління підкреслюється визначенням Колгоморова А.Н.: “кібернетика – наука, яка вивчає системи будь-якої природи, які здатні сприймати, зберігати та перероблювати інформацію, та викоритовувати її для управління.” Інформація на відміну від інших продуктів діяльності характеризується тим, шо її споживання не приводить до руйнування, а комп’ютерне відтворення копії інформаційного продукту суттєво дешевше будь-якого масового виробництва копії будь-якого іншого товару. Значення інформації в системах управління полягає в тому, що зменшення невизначеності завжди потребує додаткової інформації. Академік В.М.Глушков сформулював поняття інформаційних бар’єрів: - перший - межа складності управління економічною системою перевищує можливості однієї людини. Тоді в складі компанії повинен бути спеціаліст, який володіє знаннями і бізнесу, і інформаційних технологій; - другий - межа, коли складність задач управління системою перевищує можливості всіх людей, які приймають участь в цьому процесі. В системному аналізі визначаються та досліджуються основні інформаційні характеристики ССУ: класифікація інформаційних потоків, кількість інформації, яка потрібна для зменшення невизначеності; зміна ентропії і інш. В задачах управління складними об’єктами важливими є якісні (семантичні і прагматичні) характеристики інформації. Для їх отримання використовуються: - статистичні методи, які відображають кількісну сторону інформаційних масивів (повідомлень), але недостатньо зв’язані з методами та умовами досягнення мети функціонування системи; - методи класичної теорії управління, що використовують спеціальний формально-математичний апарат. В той же час в системному аналізі є ряд задач, які складно або неможливо формалізувати, наприклад, багатокритеріальні задачі оптимі-зації; прийняття рішень в умовах невизначеності і ін. Інформаційний підхід в задачах системного аналізу проблем управління дає можливість оцінити ряд факторів, які мають невизначений, якісний та розмитий вид. Одна з головних задач – обгрунтування та вибір математичних залежностей, які дають можливість сформувати бази даних для певної предметної області. Інформація в складних системах управління проявляється в таких формах: - (7.1)
де складовими відповідно є інформація про об’єктивні характерис-тики S (структура, властивості процеса), дестабілізуючих факторів Е зовнішнього середовища, управління та входів і виходів системи;
(7.2)
Ця інформація зосереджена в структурі системи, її елементах та вузлах, базах даних та знань, а кількість функціональних підсистем відповідає типовому процесу переробки інформації (вимірювання; спостереження; іденти-фікації; формування управлінь; координації; інформаційного обміну); -перетворена інформація
Склад цієї інформації відповідає Qn, але її форма забезпечує використання в конкретному місці в потрібний час; - інформація про управління Qy шодо реалізації контурів координатного, параметричного та структурного управління.
Поиск по сайту: |
 дійсних чисел і може бути неперевними, дискретним чи дискретно-неперервним.
дійсних чисел і може бути неперевними, дискретним чи дискретно-неперервним.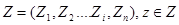 (6.13)
(6.13)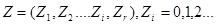 (6.15)
(6.15)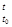 } (6.19)
} (6.19) Зовнішня схожість операторів H i G не повинна приховувати їх відмінності. Оператор Н кожному t > t0 з множини Т ставить у відповідність елемент з простору станів zÎZ. Але є системи, які видають вихідні сигнали не обов’язково в кожний момент t Î T. Щоб зменшити між ними відмінності, допускають, що множині У0 належить і пустий сигнал У0, який фізично інтерпретується як відсутність вихідного сигналу в момент t.
Зовнішня схожість операторів H i G не повинна приховувати їх відмінності. Оператор Н кожному t > t0 з множини Т ставить у відповідність елемент з простору станів zÎZ. Але є системи, які видають вихідні сигнали не обов’язково в кожний момент t Î T. Щоб зменшити між ними відмінності, допускають, що множині У0 належить і пустий сигнал У0, який фізично інтерпретується як відсутність вихідного сигналу в момент t.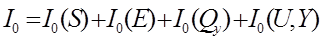 інформація повідомлення
інформація повідомлення -інформація перетворення
-інформація перетворення
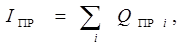 і=1,6 (7.3)
і=1,6 (7.3)