 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Колебания подрессоренной массы.
Число собственных частот колебаний системы равно числу степеней свободы. Пользуясь понятием приведенной жесткости, пренебрегая неподрессоренными массами, приведем рассматриваемый автомобиль к следующей схеме.
В реальных случаях за f можно принять ход подвески. Согласно теории колебаний движения такой системы можно описать системой уравнений
fст – статический прогиб, т.к. z1 max и z2 max, с1 и с2, т1 и т2 разные, то колебания системы будут представлять достаточно сложную картину, которую можно свести к двум типам: 1 – возвратно-поступательные относительно оси z (подпрыгивание) (система движется плоскопараллельно); 2 – вращательные относительно некоторой точки, которую называют центр упругости системы (галопирование).
Центр упругости системы – точка, которая обеспечивает только поступательное движение системы в случае приложения к ней внешней силы Р. Расстояние х от центра тяжести до центра упругости можно определить по условию равновесия системы, т.е. ΣМ = 0 = R, a – Px – R2 ·b = 0, учитывая, что R = с· f
Кроме поступательных колебаний (вверх – вниз) кузов автомобиля может совершать вращательные колебания (галопирование). Для рассмотрения условий галопирование представим модель кузова в виде трех масс.
Чтобы эта система полностью соответствовала свойствам автомобильного кузова необходимо соблюдение трех условий: 1 – т1 + т2 + т3 = тк – сумма всех масс равна подрессоренной массе кузова; 2 – центр масс системы должен совпадать с центром масс кузова, т.е. т1 · а = т2 · b 3 – момент инерции системы относительно оси «у» должен быть равен моменту инерции кузова относительно той же оси. Т.к. масса т3 расположена на оси у Jm3 = 0 Тогда Jy = m1 · а2 + m2 · b2 Из условия Jy = Jк получим m1 · а2 + m2 · b2 = mк · ρ2 где ρ – условный радиус инерции кузова. Соотношения между массами
Отношение При этом сила инерции, действующая на массу т3 (ц. т. кузова) Fu = m3 · а3 где а3 – ускорение в точке m3. Эта сила создает момент М3 относительно центра упругости М3 = m3 · а3 · х Момент М3 способствует возникновению галопирования кузова. Момент М3 будет приведен к нулю, если m3 = 0 или х = 0. Если m3 = 0, то
или ρ2 = а · b. Для большинства автомобилей ρ2 ≈ а · b с точностью до 10…15%. Если х = 0, то центр упругости совпадает с центром масс. Это достигается при условии
Из выражения следует, что коэффициенты жесткости подвесок должны быть обратно пропорциональными расстояниям центра масс кузова от осей передний и задних колес. Тогда при одинаковых прогибах передней и задней подвесок кузов автомобиля будет перемещаться вертикально без галопирования.
Поиск по сайту: |
частота вынужденный колебаний
собственные колебания
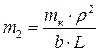
называют коэффициентом распределения подрессоренных масс. Он определяет наличие связи между колебаниями передней и задней частями кузова, т.е. кузов, совершая колебательные движения, обладает моментом инерции Jк = mк · ρ2. если не учитывать силы трения в подвеске, то этот момент инерции создает незатухающие колебания, при которых скорость и ускорения масс т, т2 и т3 будут изменяться по гармоническому закону.
