 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейные дифференциальные уравнения 1-го порядка
Сведения из теории Общий вид этих уравнений следующий: Существует готовая формула общего решения этого уравнения. Но она слишком громоздка для математически неподготовленного человека. Рассмотрим метод Бернулли для решения линейного уравнения. Он заключается в том, что решение уравнения ищется в виде произведения двух новых неизвестных функций:
Раскроем скобки:
Из левой части этого уравнения возьмем два слагаемых: одно обязательно с произведением
Вариант, когда Замечание. Если приглядеться, то левая часть этого нового уравнения с точностью до обозначения неизвестной функции удивительно напоминает левую часть исходного линейного дифференциального уравнения. Это означает, что функция
Все дальнейшие действия разберем на конкретном примере. Пример 19. Найти решение дифференциального уравнения Решение. Для перехода к новому дифференциальному уравнению заменим в исходном уравнении символ у на произведение uv, а символ у¢ на сумму
Из подчеркнутых слагаемых создаем новое уравнение
Для нахождения
Вернемся в уравнение (1). Функция По ОДЗ исходного дифференциального уравнения
Заметим, что при нахождении функции При каждом конкретном значении С получается конкретная функция, которая является решением дифференциального уравнения. А поскольку
По условию задачи нам нужно найти решение, удовлетворяющее начальным данным
График этого решения на Рис. 2 нарисован жирной линией.
Ответ. Решение задачи Коши – это функция
§4. Дифференциальные уравнения 2 – го и 3 – го порядков Сведения из теории Рассмотрим дифференциальные уравнения более высоких порядков. Они получаются тогда, когда к зависимости
4.1 Дифференциального уравнения 2 – го и 3 – го порядков, допускающие понижение порядка. Дифференциальных уравнений 2 – го и 3 – го порядков много и решаются все они по-разному. Сейчас мы рассмотрим те из них, порядок которых можно понизить до первого.
Пример 20. Найти частное решение дифференциального уравнения и вычислить значение полученной функции
Решение . Очевидно, что
Начнем решать задачу Коши, вспомнив, что
Учитывая, что
Продолжим решать задачу Коши, вернувшись от
Получим
Закончим решение задачи Коши:
Наконец окончательное решение задачи Коши примет вид:
Вычислим на калькуляторе: Замечание. Возможно, схема решения станет более очевидной, если оформить ее короче.
ß
ß
Итак, функция, являющаяся решением данного дифференциального уравнения и удовлетворяющая указанным начальным данным найдена. Осталось найти её значение при х0 = p. Ответ: Решение задачи Коши – функция
Поиск по сайту: |
 . Поясним, почему это уравнение является линейным относительно у и у¢. Обратите внимание, какие операции производятся над ними в уравнении. Переменная у умножается на функцию, зависящую только от х. То же действие выполнено и с у¢. Нет в уравнении ни у2, ни уу¢ , никаких других функций от этих переменных. Обе они входят только в первой степени, т.е. линейно. Отсюда и название уравнения.
. Поясним, почему это уравнение является линейным относительно у и у¢. Обратите внимание, какие операции производятся над ними в уравнении. Переменная у умножается на функцию, зависящую только от х. То же действие выполнено и с у¢. Нет в уравнении ни у2, ни уу¢ , никаких других функций от этих переменных. Обе они входят только в первой степени, т.е. линейно. Отсюда и название уравнения. или короче
или короче  . Для решения также понадобится заготовка
. Для решения также понадобится заготовка  . Далее, в исходное линейное уравнение подставим вместо символа у произведение
. Далее, в исходное линейное уравнение подставим вместо символа у произведение  , а вместо символа
, а вместо символа  заготовку
заготовку 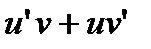 . Получим дифференциальное уравнение относительно новых неизвестных функций
. Получим дифференциальное уравнение относительно новых неизвестных функций  и
и  .
.
 .
. , а второе с символом
, а второе с символом  и создадим из них новое дифференциальное уравнение:
и создадим из них новое дифференциальное уравнение: или
или  .
. , интереса не представляет, т.к. в этом случае и функция
, интереса не представляет, т.к. в этом случае и функция  . Поэтому получаем уравнение
. Поэтому получаем уравнение  .
. -- не что иное, как частное решение однородного линейного уравнения, получающегося из неоднородного заменой правой части
-- не что иное, как частное решение однородного линейного уравнения, получающегося из неоднородного заменой правой части  на ноль.
на ноль. , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию  .
. . Получим уравнение
. Получим уравнение (1)
(1)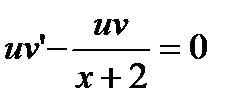 . Сократим его на
. Сократим его на  . Останется уравнение
. Останется уравнение  . А это дифференциальное уравнение с разделяющимися переменными. Решим его.
. А это дифференциальное уравнение с разделяющимися переменными. Решим его. Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ  .
. , поэтому нужно выбрать только одно конкретное значение константы С, например, С = 0. Тогда
, поэтому нужно выбрать только одно конкретное значение константы С, например, С = 0. Тогда .
. найдена нами так, что сумма подчеркнутых слагаемых обращается в ноль, а значит, из уравнения эти слагаемые исчезают. При этом вместо буквы v нужно подставить выражение
найдена нами так, что сумма подчеркнутых слагаемых обращается в ноль, а значит, из уравнения эти слагаемые исчезают. При этом вместо буквы v нужно подставить выражение  :
:  .
. , а значит, на него все уравнение можно сократить, после чего получится
, а значит, на него все уравнение можно сократить, после чего получится  . Найдем
. Найдем .
. константа С должна присутствовать обязательно. Теперь можно записать общее решение исходного дифференциального уравнения
константа С должна присутствовать обязательно. Теперь можно записать общее решение исходного дифференциального уравнения  .
. , то получается, что данное дифференциальное уравнение имеет бесконечно много решений. На Рис. 1 изображены графики пяти частных решений при
, то получается, что данное дифференциальное уравнение имеет бесконечно много решений. На Рис. 1 изображены графики пяти частных решений при  .
.
 . Геометрически это означает, что график этого решения должен проходить через точку
. Геометрически это означает, что график этого решения должен проходить через точку  . Чтобы найти это решение аналитически (т.е. его формулу), нужно в формулу общего решения подставить вместо буквы у число (-3), а вместо буквы х число 1. В результате получится одно уравнение с одним неизвестным С. В нашем примере это уравнение имеет вид:
. Чтобы найти это решение аналитически (т.е. его формулу), нужно в формулу общего решения подставить вместо буквы у число (-3), а вместо буквы х число 1. В результате получится одно уравнение с одним неизвестным С. В нашем примере это уравнение имеет вид:  . Теперь нужно найденное значение С подставить в формулу общего решения:
. Теперь нужно найденное значение С подставить в формулу общего решения: .
.

 от
от  предъявляется больше требований. Общий вид уравнений 2 – го порядка
предъявляется больше требований. Общий вид уравнений 2 – го порядка  . Общий вид уравнений 3 – го порядка
. Общий вид уравнений 3 – го порядка  .
. при
при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой. ;
;  ;
;  ;
;  ;
;  .
. . Сделаем замену
. Сделаем замену  . Тогда исходное дифференциальное уравнение 3 – го порядка
. Тогда исходное дифференциальное уравнение 3 – го порядка  примет вид
примет вид  - дифференциальное уравнение 1 – го порядка относительно неизвестной функции
- дифференциальное уравнение 1 – го порядка относительно неизвестной функции  . Это и есть понижение порядка уравнения до первого. Решить его – это значит найти все функции
. Это и есть понижение порядка уравнения до первого. Решить его – это значит найти все функции  . А это значит найти неопределенный интеграл
. А это значит найти неопределенный интеграл  .
. , где
, где  .
. :
: . Тогда
. Тогда 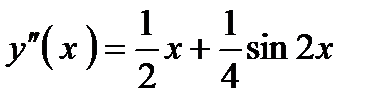 .
.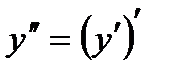 , опять сделаем замену:
, опять сделаем замену: 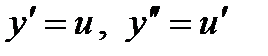 (можно даже не придумывать новую букву для замены). После замены получим новое дифференциальное уравнение 1 – го порядка:
(можно даже не придумывать новую букву для замены). После замены получим новое дифференциальное уравнение 1 – го порядка:  . Найдем его общее решение:
. Найдем его общее решение: , где
, где  .
. к
к  :
: .
. , следовательно,
, следовательно,  .
.  , где
, где  .
. .
. .
. .
.
 ,
,  Þ
Þ 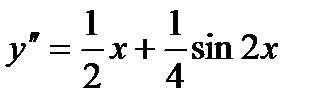
 ,
, 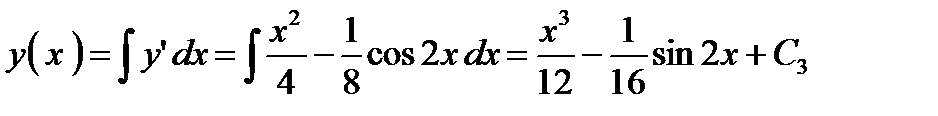 ,
,  Þ
Þ 