 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные уравнения 1 – го порядка
Сведения из теории Дифференциальное уравнение 1-го порядка (далее везде ДУ)– это уравнение вида Очень важна другая форма записи дифференциального уравнения – симметрическая или дифференциальная. Она имеет вид
Это уравнение описывает зависимость между переменными х, у и их дифференциалами Теперь определим, что же является решением ДУ.
Определение Решение ДУ – это функция
Необходимо подчеркнуть, что каждому дифференциальному уравнению удовлетворяет не одна функция Задача Коши: найти решение дифференциального уравнения
Определение Общим решением ДУ первого порядка называется бесконечное семейство функций 1. при каждом фиксированном значении С функция 2. каково бы ни было начальное условие Решение, получающееся из общего при любом конкретном значении Говорят, что найдено общее решение ДУ, если зависимость у от х получена в виде функция Говорят, что найден общий интеграл ДУ, если зависимость между у и х получена в виде уравнения
Поиск по сайту: |
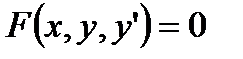 , которое содержит переменную
, которое содержит переменную  , переменную у и переменную
, переменную у и переменную  . Именно наличие символа
. Именно наличие символа  . Проблема в том, что символ у, так же как и символ
. Проблема в том, что символ у, так же как и символ  через х явно или неявно. Найти эту формулу и означает решить дифференциальное уравнение.
через х явно или неявно. Найти эту формулу и означает решить дифференциальное уравнение. .
. и
и 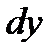 . Такая запись дифференциального уравнения не навязывает, какую переменную считать независимой, а какую зависимой. Именно поэтому форма называется симметрической. Обе формы дифференциального уравнения легко преобразуются друг в друга с помощью равенства
. Такая запись дифференциального уравнения не навязывает, какую переменную считать независимой, а какую зависимой. Именно поэтому форма называется симметрической. Обе формы дифференциального уравнения легко преобразуются друг в друга с помощью равенства  .
.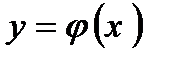 , которая при подстановке ее в дифференциальное уравнение превращает его в тождественное равенство относительно х, т.е.
, которая при подстановке ее в дифференциальное уравнение превращает его в тождественное равенство относительно х, т.е.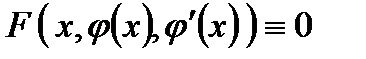 .
. , где С -- произвольная постоянная. Чтобы выделить одно нужное решение достаточно указать какое числовое значение у0 искомая функция должна принимать при заданном значении х0.
, где С -- произвольная постоянная. Чтобы выделить одно нужное решение достаточно указать какое числовое значение у0 искомая функция должна принимать при заданном значении х0. . Геометрически это означает – найти такое решение дифференциального уравнения, график которого проходит через точку
. Геометрически это означает – найти такое решение дифференциального уравнения, график которого проходит через точку 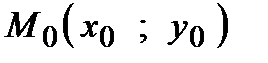 .
. удовлетворяет данному начальному условию.
удовлетворяет данному начальному условию.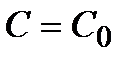 , называется частным решением
, называется частным решением  .
. (у выражено через х явно с помощью формулы
(у выражено через х явно с помощью формулы  ).
). , где С -- произвольная константа. В этом случае
, где С -- произвольная константа. В этом случае