 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегрирование по частям. Ранее уже упоминалось, что нет единого правила интегрирования произведения функций
Ранее уже упоминалось, что нет единого правила интегрирования произведения функций. Однако есть метод, который позволяет проинтегрировать некоторые виды произведений. Это метод интегрирования по частям. Его формула имеет вид
Ещё раз подчеркнем, что изначально все интегралы даны в виде При интегрировании по частям нужно выполнить следующие действия: 1)часть подынтегральной функции 2)то, что осталось от подынтегрального выражения, обозначить как дифференциал второй функции
Методические указания: 1. В заготовках при вычислении функции 2. Если подынтегральная функция является произведением многочлена на тригонометрическую функцию или многочлена на показательную функцию, то выгодно взять за функцию 3. Если подынтегральная функция содержит какую-то одну из обратных тригонометрических функций Действуя по принципу «Лучше один раз увидеть, чем сто раз услышать», переходим к примерам.
Пример 10.Найти интеграл Решение.
Пример 11. Найти интеграл Решение.
§2.Определенный интеграл
Сведения из теории Понятие определенного интеграла возникло задолго до появления понятий производной, первообразной и неопределенного интеграла. Схема введения этого понятия достаточно проста. Есть функция 1. Этот отрезок произвольным образом разбивается на 2. На каждом таком интервале произвольно выбирается точка 3. Затем строится интегральная сумма 4. Далее разбиение отрезка 5. Последовательность разбиений порождает последовательность интегральных сумм
Вычисление определенного интеграла по определению, т.е. как предел интегральных сумм, задача очень сложная. К счастью, гениальные математики прошлого Ньютон и Лейбниц установили связь определенного интеграла с первообразной для функции
Из формулы видно, что достаточно найти какую-то одну первообразную функцию 2.1. Методы вычисления определенного интеграла Следует подчеркнуть, что с технической точки зрения вычисление определенного интеграла мало чем отличается от вычисления неопределенного интеграла. Поэтому для нахождения первообразной используем все методы, описанные ранее для неопределенного интеграла. Пример 12.Вычислить определенный интеграл Решение. Найдем сначала неопределенный интеграл
Вернемся к определенному интегралу. Для использования формулы Ньютона-Лейбница достаточно знать какую-то одну конкретную первообразную
Ответ.
Замечание. Этот интеграл можно найти и с помощью замены переменной. Подчеркнем, что в определенном интеграле необязательно возвращаться к старой переменной Пример 13.Вычислить определенный интеграл Решение.
Сведения из теории Формула интегрирования по частям для определенного интеграла имеет вид
Пример 14. Вычислить определенный интеграл Решение. Подынтегральная функция является отношением двух разнотипных функций, поэтому определенный интеграл от нее можно взять только по частям.
2.2. Вычисление площадей плоских фигур с помощью определенного интеграла
Прежде всего, плоская фигура
Тогда ее площадь вычисляется по формуле
Замечание. Не нужно разбивать область на части, лежащие выше и ниже оси ОХ. Берется один интеграл от разности функций, задающих верхнюю и нижнюю границы. Пример 15. Найти площадь плоской фигуры Решение. Прежде всего, следует нарисовать область

Запишем область  системой двух неравенств, т.е. системой двух неравенств, т.е.
Ответ
Поиск по сайту: |
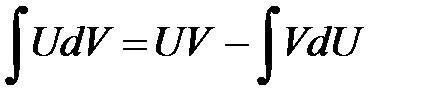 .
.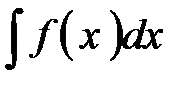 . Структуру для интегрирования по частям вы должны построить сами.
. Структуру для интегрирования по частям вы должны построить сами.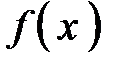 обозначить как новую функцию
обозначить как новую функцию 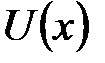 и приготовить заготовку
и приготовить заготовку 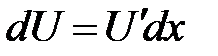 ;
;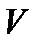 (которая, вообще-то, изначально неизвестна) и найти эту функцию по формуле
(которая, вообще-то, изначально неизвестна) и найти эту функцию по формуле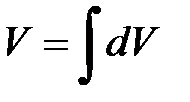 .
.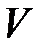 в неопределенном интеграле берем константу
в неопределенном интеграле берем константу 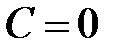 .
. именно многочлен, т.к. он при дифференцировании упрощается. Тригонометрические и показательные функции не упростятся, сколько бы их ни дифференцировали или интегрировали.
именно многочлен, т.к. он при дифференцировании упрощается. Тригонометрические и показательные функции не упростятся, сколько бы их ни дифференцировали или интегрировали.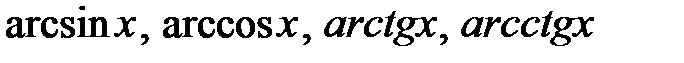 или логарифмическую функцию
или логарифмическую функцию 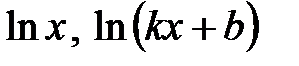 , то выгодно именно их выбрать в качестве функции
, то выгодно именно их выбрать в качестве функции  , т.к. известно как их дифференцировать.
, т.к. известно как их дифференцировать. .
.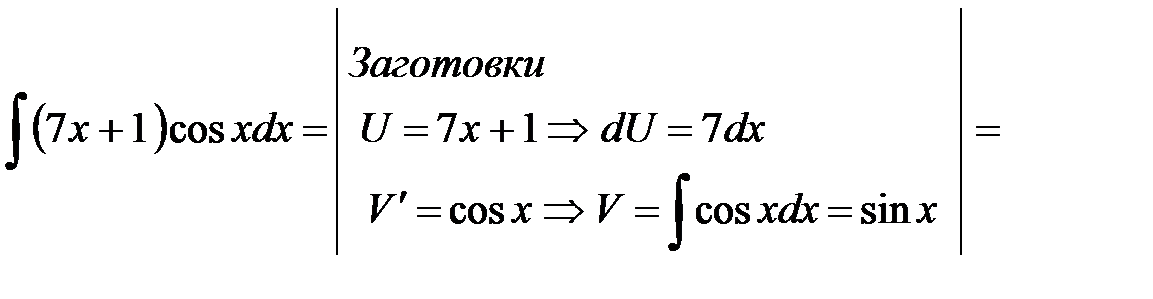
 .
. .
.
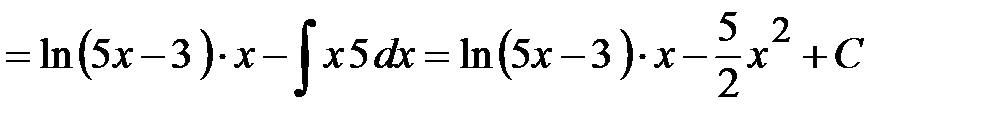 .
.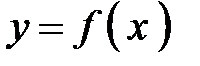 . Она определена и непрерывна на отрезке
. Она определена и непрерывна на отрезке 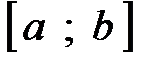 .
.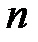 интервалов
интервалов 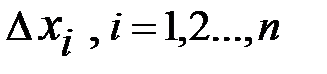 .
. . В ней вычисляется значение функции
. В ней вычисляется значение функции 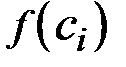 .
.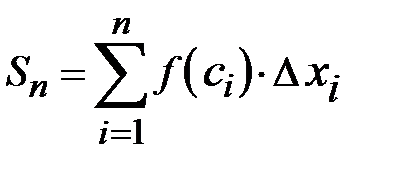 .
.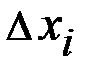 возрастает, т.е.
возрастает, т.е. 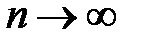 .
.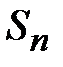 . Если эта последовательность стремится к конечному пределу, то он и называется определенным интегралом. Символически это записывается так
. Если эта последовательность стремится к конечному пределу, то он и называется определенным интегралом. Символически это записывается так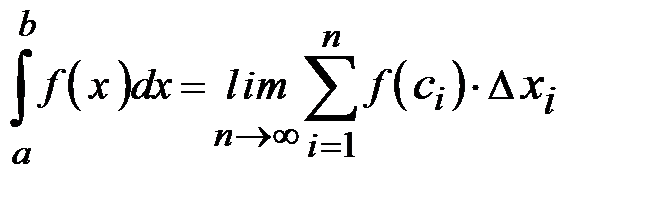 .
. . Созданная ими формула известна всему образованному человечеству как формула Ньютона-Лейбница. Она имеет вид
. Созданная ими формула известна всему образованному человечеству как формула Ньютона-Лейбница. Она имеет вид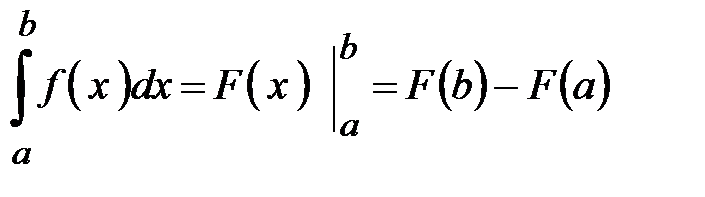 .
.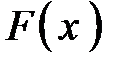 для функции
для функции 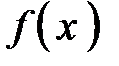 . Тогда её приращение
. Тогда её приращение  и будет равно определенному интегралу.
и будет равно определенному интегралу.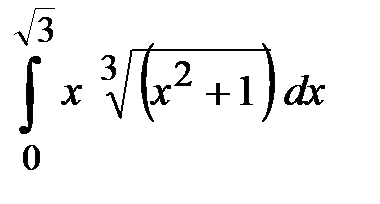 . Результат записать в виде десятичной дроби с двумя знаками после запятой.
. Результат записать в виде десятичной дроби с двумя знаками после запятой. , используя метод подведения под знак дифференциала:
, используя метод подведения под знак дифференциала: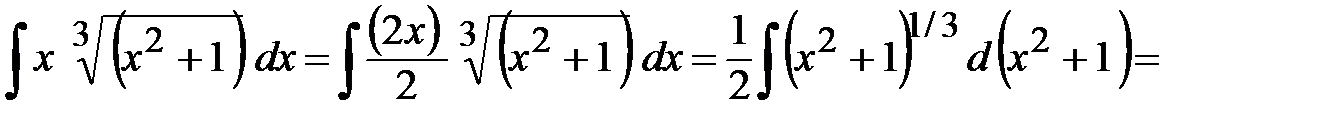
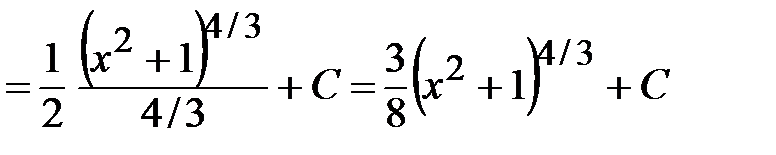 .
. . Для простоты выберем ту, которая получается из неопределенного интеграла при
. Для простоты выберем ту, которая получается из неопределенного интеграла при  , т.е.
, т.е.  . Тогда
. Тогда 

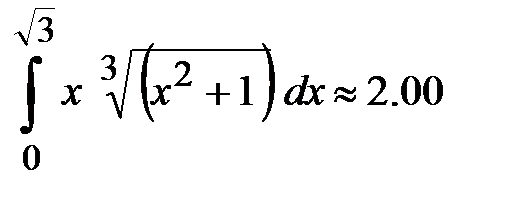
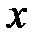 . Для этого достаточно пересчитать пределы интегрирования для новой переменной. Решим таким образом предыдущий пример.
. Для этого достаточно пересчитать пределы интегрирования для новой переменной. Решим таким образом предыдущий пример.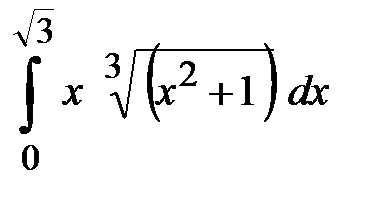 .
.
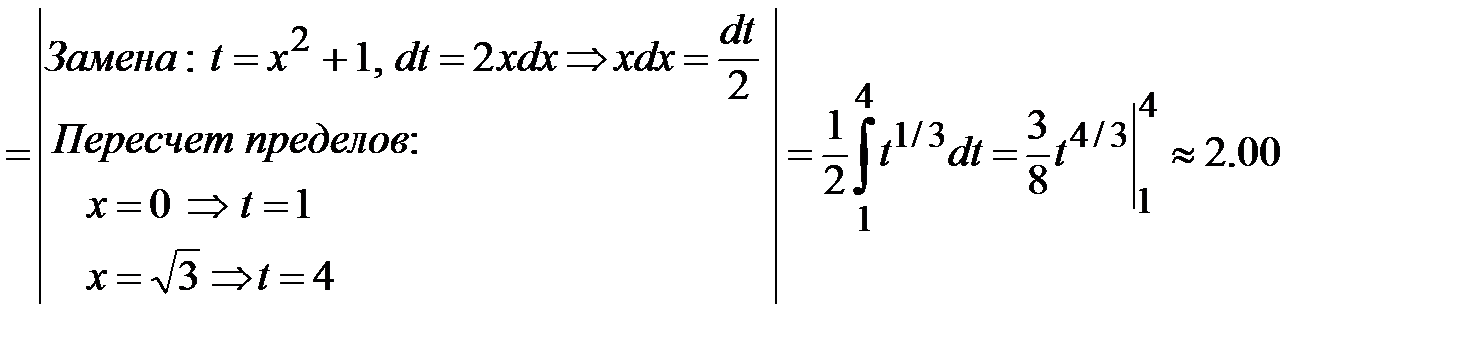
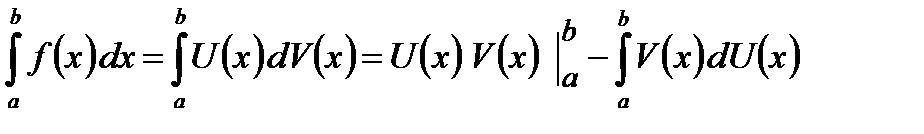
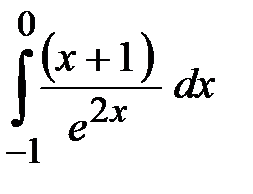 . Результат записать в виде десятичной дроби с двумя знаками после запятой.
. Результат записать в виде десятичной дроби с двумя знаками после запятой.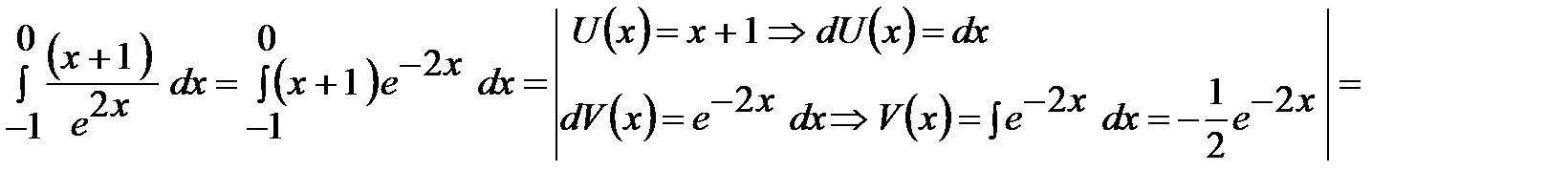

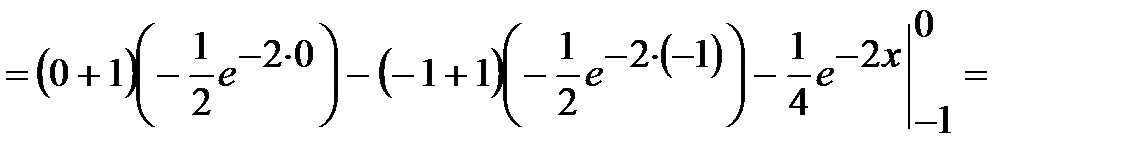
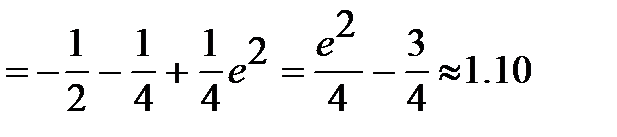
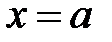 самых левых точек области и абсциссу
самых левых точек области и абсциссу 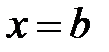 самых правых точек области. Тогда для любой точки
самых правых точек области. Тогда для любой точки 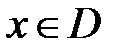 верно неравенство
верно неравенство  . Значения этих абсцисс и станут нижним и верхним пределами интеграла. Далее нужно найти формулу верхней границы
. Значения этих абсцисс и станут нижним и верхним пределами интеграла. Далее нужно найти формулу верхней границы 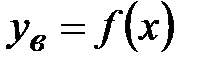 и формулу нижней границы
и формулу нижней границы  . При этом на всем отрезке
. При этом на всем отрезке 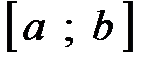 должно выполняться неравенство
должно выполняться неравенство  (верхняя и нижняя границы не должны пересекаться). После выполнения этих шагов фигура
(верхняя и нижняя границы не должны пересекаться). После выполнения этих шагов фигура  может быть записана системой двух неравенств
может быть записана системой двух неравенств
 .
.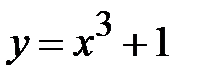 ;
;  ;
; 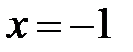 ;
;  .
.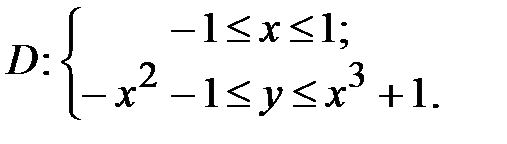 Тогда площадь
Тогда площадь  находится как определенный интеграл
находится как определенный интеграл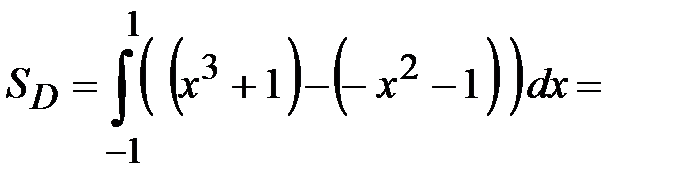

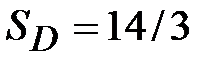 .
.