 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные уравнения с разделяющимися переменными
Сведения из теории Справедливости ради следует заметить, что очень редко ДУ сразу дается в симметрической форме с разделенными переменными. Рассмотрим уравнения, которые можно привести к такому виду. Пусть ДУ приведено к симметрической форме
Новый вид уравнения
Пример 17. Решить уравнение Решение. Сначала преобразуем уравнение так, чтобы символы
Теперь представим в виде произведений выражения перед
Разделим переменные:
Проинтегрируем: Þ Полученное уравнение уже является общим решением дифференциального уравнения или иначе общим интегралом. В принципе можно считать уравнение решенным. Однако, решение очень громоздкое. Его можно упростить. Во всех дальнейших преобразованиях нам понадобится один искусственный прием переобозначения константы С. Как известно, константа С пробегает все значения от
Последнее уравнение является более компактной формой общего интеграла. На этом решение дифференциального уравнения можно закончить. Ответ. Общий интеграл дифференциального уравнения имеет вид
Замечание. В примере 2 не сказано конкретно, что нужно найти – общий интеграл или общее решение. Если общий интеграл, то пример 2 решен до конца. Если же подразумевалось общее решение, то тогда из уравнения
Каждая из полученных функций является общим решением дифференциального уравнения.
Разберем, как решать уравнение с разделяющимися переменными, заданное не в симметрической форме, а в виде Пример 18. Найти общий интеграл дифференциального уравнения
Решение. Перейдем к симметрической форме, используя равенство
Разделим переменные:
Проинтегрируем полученное уравнение :
Последнее уравнение является общим интегралом дифференциального уравнения. Ответ: Общий интеграл дифференциального уравнения
Поиск по сайту: |
 . В нем можно разделить переменные, если выражения
. В нем можно разделить переменные, если выражения  и
и  можно представить в виде произведения двух сомножителей, каждое из которых зависит или только от х или только от у, т.е.
можно представить в виде произведения двух сомножителей, каждое из которых зависит или только от х или только от у, т.е. ,
,  .
. . Для разделения переменных нужно обе части уравнения поделить (или умножить) на те сомножители, которые «мешают».
. Для разделения переменных нужно обе части уравнения поделить (или умножить) на те сомножители, которые «мешают».



 и
и 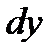 присутствовали по одному разу:
присутствовали по одному разу: Þ
Þ  .
.
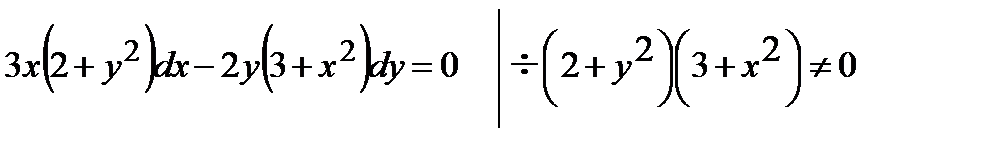

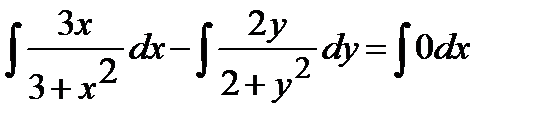 Þ
Þ  Þ
Þ  Þ
Þ
 до
до  и неважно каким способом. Поэтому зададим нужный нам способ изменения С. В данном конкретном примере выгодно заменить С на
и неважно каким способом. Поэтому зададим нужный нам способ изменения С. В данном конкретном примере выгодно заменить С на  , где
, где  . В дальнейшем замену константы С на другой вид будем обозначать символом
. В дальнейшем замену константы С на другой вид будем обозначать символом  . Для преобразований используем свойства логарифмов.
. Для преобразований используем свойства логарифмов. Þ
Þ  Þ
Þ  .
. Þ
Þ  .
.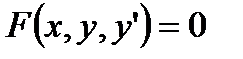 . Первое, что нужно сделать – это перейти к симметрической форме, заменив символ
. Первое, что нужно сделать – это перейти к симметрической форме, заменив символ  на
на  . Покажем это на конкретном примере.
. Покажем это на конкретном примере. .
. :
: Þ
Þ  .
. Þ
Þ 
 Þ
Þ  Þ
Þ  .
.