 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные уравнения с разделенными переменными
Сведения из теории Традиционно изложение методов решения дифференциальных уравнений начинается с уравнений с разделенными переменными. Это обязательно уравнение в симметрической форме, у которого выражение, стоящее перед символом
Перенесем в правую часть слагаемое, содержащее Прежде чем рассматривать пример, оговорим одну «вольность», допустимую при решении дифференциального уравнения с разделенными переменными. Пусть уравнение приведено к виду Подчеркнем конструктивные особенности дифференциального уравнения в симметрической форме: 1. символы 2. символы 3. неважно, в каком порядке следуют слагаемые с 4. лучше, если символы
Пример16. Найти общий интеграл дифференциального уравнения
Решение. Очевидно, что наше уравнение содержит два слагаемых с символом
Проинтегрируем его: Ответ. Общий интеграл дифференциального уравнения Замечание. Если бы в примере 1 требовалось найти общее решение дифференциального уравнения, то получение уравнения
Поиск по сайту: |
 , зависит только от переменной
, зависит только от переменной  , а выражение, стоящее перед
, а выражение, стоящее перед 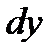 , зависит только от переменной
, зависит только от переменной  (слово «разделить» здесь означает не арифметическую операцию деления, а процедуру отделения выражений, содержащих только х от выражений, содержащих только у). Короче, уравнение с разделенными переменными имеет вид
(слово «разделить» здесь означает не арифметическую операцию деления, а процедуру отделения выражений, содержащих только х от выражений, содержащих только у). Короче, уравнение с разделенными переменными имеет вид .
. . Выражения слева и справа рассматриваем как дифференциалы двух неизвестных функций, каждая из которых зависит только от одной переменной, а именно
. Выражения слева и справа рассматриваем как дифференциалы двух неизвестных функций, каждая из которых зависит только от одной переменной, а именно  , а
, а  . Если дифференциалы функций равны, то сами функции могут отличаться только на константу. Следовательно,
. Если дифференциалы функций равны, то сами функции могут отличаться только на константу. Следовательно,  , где
, где  - некоторая константа. Как найти функции
- некоторая константа. Как найти функции  и
и  ? Да очень просто.
? Да очень просто.  -- это какая - либо первообразная для функции
-- это какая - либо первообразная для функции  , а
, а  .
. . При этом неважно по какой переменной вы возьмете интеграл от нуля: по х или по
. При этом неважно по какой переменной вы возьмете интеграл от нуля: по х или по  . Он все равно будет равен константе С.
. Он все равно будет равен константе С. .
. влево, сгруппируем слагаемые с
влево, сгруппируем слагаемые с  Þ
Þ  Þ
Þ 
 . В результате получим уравнение
. В результате получим уравнение  . Очевидно, что переменные х и у входят в это уравнение вперемешку. Переменная у не выражена явно как функция переменной х. Поэтому это уравнение является общим интегралом дифференциального уравнения. Получение этого уравнения можно считать концом решения.
. Очевидно, что переменные х и у входят в это уравнение вперемешку. Переменная у не выражена явно как функция переменной х. Поэтому это уравнение является общим интегралом дифференциального уравнения. Получение этого уравнения можно считать концом решения. нужно из уравнения
нужно из уравнения  .
.