 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производная по направлению функции двух переменных. Градиент функции двух переменных
Пример 30. Представьте себе, что Вы проводите геодезические работы с использованием карты некоторой местности. Предположим, что высота каждой точки этой местности над уровнем моря задана как функция координат этой точки, например, 1) параллельно оси ОХ; 2) параллельно оси ОУ; 3) параллельно биссектрисе первого координатного угла; 4) параллельно вектору 5) в направлении градиента. Решение 1) Тот факт, что из точки М0 (1; 2) мы двигаемся параллельно оси ОХ означает, что переменная х меняется, а переменная у фиксирована, а именно, у = 2 . Такое передвижение по карте дает кривую линию на поверхности. Крутизна этой линии определяется углом j1, который образует касательная, проведенная к этой линии в точке поверхности, соответствующей точке М0 на карте. Тангенс этого угла равен значению частной производной по х функции
Тогда крутизна в направлении параллельном оси ОХ равна углу 2) Обозначим j2 крутизну (угол) поверхности в точке М0 в направлении параллельном оси ОУ. Тогда
В результате получим 3) При движении параллельно биссектрисе первого координатного угла изменяются уже обе переменные. Обозначим крутизну в этом направлении как угол j3. Его тангенс равен производной от формулы высоты по направлению указанной биссектрисы в точке М0. Напомним формулу производной функции двух переменных по направлению вектора
Ранее нашли частные производные 4) Обозначим крутизну в направлении вектора Вычислим:
В направлении вектора 5) Обозначим крутизну в направлении градиента как угол j5. Напомним, что градиент – это вектор, который находится по следующей формуле
Пересчитаем направляющие косинусы:
Тогда
Обратите внимание, крутизна в направлении градиента получилась самой большой. Это явилось подтверждением того факта, что в направлении градиента функция двух переменных растет с самой большой скоростью, которая численно равна длине вектора-градиента. В геодезической трактовке это означает, что в точке М0 (1; 2) в направлении вектора-градиента крутизна поверхности самая большая.
Поиск по сайту: |
 . (Конечно, это предположение является искусственным и вряд ли на практике высота задается формулой). Мы определили свое положение на карте в точке
. (Конечно, это предположение является искусственным и вряд ли на практике высота задается формулой). Мы определили свое положение на карте в точке  . Требуется определить крутизну подъема поверхности (угол в градусах) в разных направлениях, исходящих из точки М0, а именно:
. Требуется определить крутизну подъема поверхности (угол в градусах) в разных направлениях, исходящих из точки М0, а именно: ;
; в точке М0.
в точке М0.
 . Положительное значение угла говорит о том, что в направлении параллельном оси ОХ высота растет (подъем).
. Положительное значение угла говорит о том, что в направлении параллельном оси ОХ высота растет (подъем). .
. . Отрицательное значение угла говорит о том, что в направлении параллельном оси ОУ высота уменьшается (склон).
. Отрицательное значение угла говорит о том, что в направлении параллельном оси ОУ высота уменьшается (склон). .
.
 и
и  . Как известно, биссектриса первого координатного угла образует с осями координат углы по 45°. Следовательно,
. Как известно, биссектриса первого координатного угла образует с осями координат углы по 45°. Следовательно,  и
и  . Обозначим направление по биссектрисе как вектор
. Обозначим направление по биссектрисе как вектор 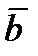 . Тогда
. Тогда 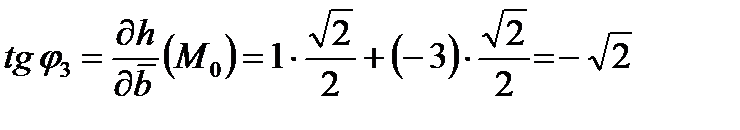 , откуда
, откуда  . Судя по знаку этой производной, в направлении биссектрисы высота тоже убывает.
. Судя по знаку этой производной, в направлении биссектрисы высота тоже убывает. и
и  . Воспользуемся формулами
. Воспользуемся формулами  :
:  .
. .
. , откуда
, откуда 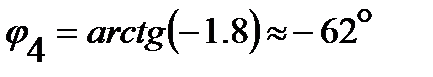 .
. .
. ,
, 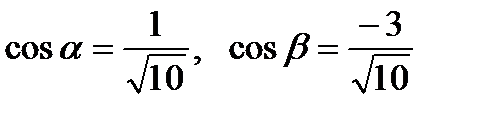
 .
. .
.