 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие неопределенного интеграла. Методические указания и контрольные заданияСтр 1 из 13Следующая ⇒
МАТЕМАТИКА Методические указания и контрольные задания для студентов заочной ускоренной формы обучения строительных специальностей (2 семестр)
Факультет инженерно-строительный Для всех специальностей
Вологда 2012
УДК: 511.147:511.61/62
Математика: методические указания и контрольные задания для студентов заочной ускоренной формы обучения строительных специальностей (2 семестр). Вологда: ВоГТУ, 2012.
Составители: Н.В. Степанова, канд. физ.-мат. наук, доцент
Рецензент:
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил:
1. Студент должен выполнять контрольные задания по варианту, в двойном номере которого вторая цифра совпадает с последней цифрой его шифра - номера его зачетной книжки. Если номер заканчивается цифрой 0, то студент должен выполнять вариант №10. 2. Каждая контрольная работа должна быть выполнена в отдельной тетради в клеточку чернилами синего или черного цвета. 3. Образец оформления титульного листа (обложки) тетради приведен на доске объявлений деканата ФЗДО. 4. В работу должны быть включены все задачи, указанные в задании. Работы, содержащие не все задачи задания, а также задачи не своего варианта, не рецензируются. 5. Задачи нужно решать в том порядке, в котором они указаны в контрольной работе. 6. Перед решением каждой задачи надо полностью выписать ее условие. 7. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи (рисунки). 8. Компьютерное оформление работы не рецензируется. 9. Возвращенная прорецензированная незачтенная работа исправляется студентом; исправление записывается в конце работы. Вносить исправления в проверенный текст работы - запрещается.
Введение Настоящие методические указания служат руководством для студентов заочников при выполнении контрольных заданий, запланированных во 2 учебном семестре. С их помощью студент - заочник сможет самостоятельно разобраться в основных типах задач и справиться с выполнением контрольных заданий. Неопределенный интеграл.
Понятие неопределенного интеграла. Сведения из теории Для начала вспомним задачу дифференцирования: дана функция Теперь будем решать обратную задачу: дана функция Определение Функция
Первообразная функция обладает двумя свойствами. Свойство 1. Если какая-то конкретная функция Свойство 2. Пусть найдены две первообразных функции Из этих двух свойств получается важное следствие. Чтобы найти все первообразные функции для функции Фраза «Неопределенный интеграл от функции
функции Запомните термины:
Таблица основных неопределенных интегралов Неопределенные интегралы от основных элементарных функций приведены в следующей таблице.
Теперь сформулируем правила, которые позволяют интегрировать функции, получающиеся из простейших элементарных функций с помощью умножения на число, сложения и вычитания. 1. Постоянный множитель в подынтегральной функции можно выносить за знак интеграла, т.е.
2. Интеграл от суммы или разности функций равен сумме (или соответственно разности ) интегралов от этих функций, т.е.
К сожалению, нет единых правил для интегрирования произведения и частного функций. Также нет единого правила интегрирования сложной функции. По этой причине приходится признать, что интегрирование функций – операция более сложная, чем дифференцирование.
Поиск по сайту: |
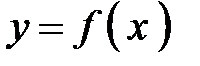 . Найти новую производную функцию
. Найти новую производную функцию  .
. . Нужно найти формулу этой функции
. Нужно найти формулу этой функции  .
. .
. , где
, где  также является первообразной для функции
также является первообразной для функции  и
и  для одной и той же функции
для одной и той же функции  , т.е.
, т.е.  .
.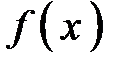 » записывается символами
» записывается символами 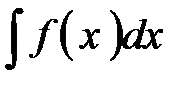 . Тогда понятие неопределенного интеграла символьно записывается равенством
. Тогда понятие неопределенного интеграла символьно записывается равенством , где
, где  -- какая - то одна первообразная для
-- какая - то одна первообразная для , а
, а  .
. -- подынтегральная функция,
-- подынтегральная функция, -- подынтегральное выражение,
-- подынтегральное выражение, -- переменная интегрирования.
-- переменная интегрирования.

 , если
, если  .
.











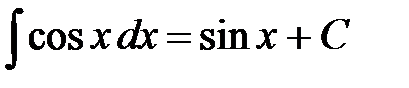



 .
. .
.